Integració numèrica

En càlcul, la integració numèrica consisteix en una família d'algorismes per a calcular el valor numèric d'una integral definida, per extensió, el terme de vegades es fa servir també per a descriure la solució numèrica d'equacions diferencials ordinàries. Aquest article se centra en el càlcul d'integrals definides. El terme quadratura numèrica (sovint abreviat a quadratura) és més o menys sinònim d'integració numèrica, especialment si s'aplica a integrals d'una dimensió tot i que pel cas de dues o més dimensions (integral múltiple) també es fa servir.

El problema bàsic al que s'adreça la integració numèrica és del de calcular una solució aproximada a una integral definida.

$\int _{a}^{b}\!f(x)\,dx.$

Si f(x) és una funció contínuament derivable sobre un nombre petit de dimensions i els límits d'integració són afitats, llavors hi ha molts mètodes excel·lents per a aproximar la integral amb una precisió arbitrària.

Integració numèrica emprant el mètode de Monte Carlo: Els nodes es distribueixen emprant una distribució de probabilitat uniforme. Als nodes nou són blau marí, els vell blau cel. El valor de la integral tendeix cap a 3,32

Motius per a la integració numèrica

Hi ha molts motius per a emprar la integració numèrica. Pot ser que l'integrand f(x) només sigui conegut a determinats punts, per exemple obtinguts per mostreig. Alguns sistemes integrats i altres aplicacions informàtiques pot ser que necessitin integració numèrica per aquest motiu.

Pot ser que es conegui la fórmula de l'integrand, però pot ser que sigui difícil o impossible de trobar una primitiva que sigui una funció elemental. Un exemple d'això és f(x) = exp(−x²), la primitiva de la qual no es pot escriure de forma elemental.

De vegades és possible trobar la primitiva simbòlicament, però pot ser més fàcil de calcular la integral numèricament que calcular els valors de la primitiva. Aquest pot ser el cas per exemple si la primitiva ve donada per una sèrie o un producte infinits, o si la seva avaluació requereix una funció especial l'algorisme per avaluar la qual no es té disponible.

Mètodes per a integrals d'una dimensió

Els mètodes d'integració numèrica troben un valor aproximat de la integral definida. Amb un error que és la diferència entre el valor que donen i el valor exacte.

Les diferències entre els diferents mètodes es basen principalment en la forma de trobar l'aproximació de la integral i en alguns casos la forma d'anar afinant el càlcul per a reduir l'error estimat.

Una part important de l'anàlisi de la integració numèrica és l'estudi del comportament de l'aproximació de l'error com a funció del nombre d'avaluacions de la funció integrand.

Val a dir que el problema només té interès si no és possible conèixer amb exactitud el valor de l'error. L'error per definició és la diferència entre el valor aproximat i el valor exacte. En els casos on es pot conèixer l'error, n'hi ha prou amb afegir-lo al valor aproximat per a obtenir el valor exacte. Però en aquests casos no cal una integració numèrica. Per tant els mètodes treballen o bé amb fites superiors de l'error o bé amb valors estimats de l'error.

Entre dos mètodes que tenen el mateix error, es considera superior el que necessita un nombre inferior d'avaluacions de la funció.

El fet de reduir el nombre d'avaluacions de la funció integrand redueix el nombre d'operacions aritmètiques implicades. Això redueix el temps de càlcul. En els casos en què els càlculs es fan amb operacions de coma flotant (que són la majoria) el fet de reduir el nombre d'operacions també redueix l'error d'arrodoniment total.

La integració numèrica per la 'força bruta' es pot fer, si la funció integrand té un comportament raonablement bo (per exemple és contínua), a base d'avaluar l'integrand amb increments molt petits.

Mètodes basats en funcions d'interpolació

Hi ha una extensa família de mètodes que es basen a aproximar la funció a integrar $f(x)$ per una altra funció $g(x)$ de la qual es coneix la integral exacta. La funció que substitueix l'original es troba de forma que, en un cert nombre de punts tingui el mateix valor que l'original. Com que els punts extrems formen part sempre d'aquest conjunt de punts, de la nova funció se'n diu una interpolació de la funció original. (quan els punts extrems no es fan servir per trobar la funció que substitueix l'original llavors se'n diu extrapolació). Típicament aquestes funcions són polinomis.

Il·lustració del mètode rectangular.

El mètode més senzill d'aquesta classe és el de fer que la funció d'interpolació sigui una funció constant (un polinomi de grau zero) que passa pel punt ((a+b)/2, f((a+b)/2)). D'aquest mètode se'n diu el mètode del punt mitjà o el mètode rectangular.

${\begin{aligned}&g(x)=f\left({\frac {a+b}{2}}\right)\\&\int _{a}^{b}{f\left(x\right)dx\approx }\int _{a}^{b}{g\left(x\right)dx=\left(b-a\right)}f\left({\frac {a+b}{2}}\right)\\\end{aligned}}$

Il·lustració del mètode trapezial.

La funció d'interpolació pot ser també una funció afí (un polinomi de grau 1) Que passa pels punts extrems (a, f(a)) and (b, f(b)).

D'aquest mètode se'n diu el mètode trapezial.

$g(x)=f(a)+{\frac {f(b)-f(a)}{b-a}}(x-a)$

$\int _{a}^{b}f(x)\,dx\approx (b-a)\,{\frac {f(a)+f(b)}{2}}.$

Il·lustració del mètode de Simpson.

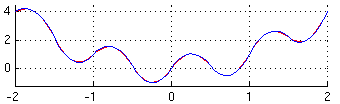
Per a cada un d'aquests mètodes, es pot aconseguir una aproximació més exacta a base de trencar l'interval [a, b] en n subintervals, calculant una aproximació per cada un dels subintervals, i després sumant tots els resultats (si l'amplada de l'interval és constant es pot treure factor comú de l'amplada de l'interval i multiplicar al final, d'aquesta forma es redueix el nombre d'operacions). D'això se'n diu un mètode compost, mètode estes, or mètode iterat. Per exemple, el mètode trapezial compost es pot establir com

$\int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{n}}\left({f(a)+f(b) \over 2}+\sum _{k=1}^{n-1}f\left(a+k{\frac {b-a}{n}}\right)\right)$

On els subintervals tenen la forma [k h, (k+1) h], amb h = (b−a)/n i k = 0, 1, 2, …, n−1.

La interpolació amb polinomis avaluats a punts equidistants en [a, b] porten a les fórmules de Newton-Cotes, de les quals les regles rectangular i trapezial en són exemples. EL mètode de Simpson, que es basa en polinomis de segon grau és també una fórmula de Newton-Cotes.

Els mètodes de quadratura que utilitzen punts equidistants tenen la propietat molt convenient de què al subdividir els intervals el nou conjunt de punts conté l'anterior, d'aquesta forma els valors de la funció integrand es poden reutilitzar (no cal tornar-los a calcular).

Si es permet que els intervals entre punts d'interpolació variïn, es troba un altre grup de fórmules de quadratura, com les fórmules de quadratura de Gauss. Una quadratura de Gauss és normalment més exacta que una de Newton-Cotes amb la mateixa quantitat d'avaluacions de la funció, si l'integrand és suau (és a dir és derivable molts cops). Altres mètodes de quadratura amb intervals variables inclouen la quadratura de Clenshaw-Curtis i els mètodes de quadratura de Fejér.

Els punts de la quadratura de Gauss no són reutilitzables, però els de la quadratura de Gauss-Kronrod, que hi està estretament relacionada, sí que són reutilitzables. Els punts de la quadratura de Clenshaw-Curtis també són reutilitzables.

Algorismes adaptatius

Article principal: Quadratura adaptativa

Si f(x) no té moltes derivades a tots els punts, o si les derivades esdevenen grans (el gràfic de la funció és molt proper a una recta vertical), llavors la quadratura de Gauss sovint és insuficient. En aquest cas un algorisme com el següent pot donar millors resultats:

// Aquest algorisme calcula la integral definida d'una funció, des de 0 fins a 1,
// de forma adaptativa, a base de triar passos més petits en les zones properes 
// als punts problemàtics.
// Assignar a inicial_h la mida inicial del pas.
x:=0
h:=inicial_h
acumulador:=0
FER MENTRE x<1.0
SI x+h>1.0 LLAVORS
h=1.0-x
FI SI
SI l'error de quadratura de f(x) sobre [x,x+h] és massa gran LLAVORS
Fer h més petit
ALTRAMENT
acumulador:=acumulador + quadratura de f sobre [x,x+h]
x:=x+h
SI l'error de quadratura de f(x) sobre [x,x+h] és molt petit LLAVORS
Fer h més gran
FI SI
FI SI
FI FER MENTRE
RETORNA acumulador

Alguns detalls de l'algorisme requereixen una anàlisi curosa. En molts casos, estimar l'error de la quadratura sobre un interval per a una funció f(x) no és obvi. Una solució popular és emprar dos mètodes de quadratura diferents i fer servir la diferència com una estimació de l'error. L'altre problema és decidir què signifiquen "massa gran" i "molt petit". Un criteri local per a "massa gran" és que l'error de quadratura no ha de ser més gran que $t\cdot h$ on el nombre real t, és la tolerància que es desitja establir per a l'error global. Llavors altre cop, si h ja és minúscul, pot no valer la pena de fer-lo més petit, encara que l'error de quadratura sigui aparentment gran. Un criteri global és que la suma dels errors de tots els intervals ha de ser més petit que t. D'aquest tipus d'anàlisi de l'error se'n anomena habitualment "a posteriori" donat que es calcula l'error després d'haver calculat l'aproximació.

Les heurístiques per a la quadratura adaptativa es discuteixen a Forsythe i cols. (Secció 5.4).

Mètodes d'extrapolació

L'exactitud d'una quadratura de Newton-Cotes és generalment funció del nombre de punts d'avaluació. EL resultat és normalment més exacte a mesura que el nombre de punts d'avaluació augmenta, O, el que és equivalent, a mesura que la distància entre punts disminueix. És natural de qüestionar quin seria el resultat si es permetés que el pas s'apropés a zero. Aquesta pregunta es pot respondre a base de extrapolar el resultat que s'obté a partir de dos o més mides de pas petites però diferents de zero (vegeu extrapolació de Richardson). La funció d'extrapolació pot ser un polinomi o una funció racional. Els mètodes d'extrapolació es descriuen amb més detall per Stoer i Bulirsch (Secció 3.4).

Estimació conservadora (a priori) de l'error

Sia f una funció amb una derivada primera afitada en [a,b]. Llavors el teorema del valor mitjà per a f, on $x<b$, diu

$(x-a)f'(y_{x})=f(x)-f(a)\,$

Per algun $y_{x}$ de [a,x] depenent de x. Si s'integra en x des de a fins a b als dos cantons i es prenen valors absoluts, s'obté

$\left|\int _{a}^{b}f(x)\,dx-(b-a)f(a)\right|=\left|\int _{a}^{b}(x-a)f'(y_{x})\,dx\right|$

Encara es pot aproximar més la integral del cantó dret a base de ficar el valor absolut dins del integrand, i substituinr el terme en f' per una fita superior:

$\left|\int _{a}^{b}f(x)\,dx-(b-a)f(a)\right|\leq {(b-a)^{2} \over 2}\sup _{a\leq x\leq b}\left|f'(x)\right|$ (**)

(Vegeu suprem.) A partir d'aquí, si s'aproxima la integral ∫_a^bf(x)dx pel mètode de quadratura (b−a)f(a) l'error no és més gran que el cantó dret de (**). Això es pot convertir en una anàlisi de l'error per al sumatori de Riemann (*), donada una fita superior de

${n^{-1} \over 2}\sup _{0\leq x\leq 1}\left|f'(x)\right|$

Per al terme d'error d'aquesta particular aproximació. (Fixeu-vos que aquest és precisament l'error que s'ha calculat pel cas $f(x)=x$.) Emprant més derivades, i a base de anar pessigant la quadratura, es pot fer una anàlisi de l'error similar emprant una sèrie de Taylor (emprant un sumatori parcial amb el terme residual) per f. Aquesta anàlisi de l'error dona una fita superior estricta de l'error, si les derivades de f estan disponibles.

Aquest mètode d'integració es pot combinar amb l'aritmètica d'intervals per a produir demostracions computacionals i càlculs verificats.

Integrals múltiples

Els mètodes de quadratura que s'han comentat fins aquí s'han dissenyat tots per a calcular integrals d'una dimensió.

Per a calcular integrals de diverses dimensions, un enfocament és expressar la integral múltiple com a repetició d'integrals d'una dimensió fent ús del teorema de Fubini.

Aquest enfocament porta a una quantitat d'avaluacions de la funció que creix exponencialment a mesura que creix el nombre de dimensions. Es coneixen dos mètodes per a superar aquesta anomenada maledicció de la dimensió.

Montecarlo

Article principal: Integració de Montecarlo

Els mètodes de Montecarlo i mètodes de quasi-Montecarlo són fàcils d'aplicar a integrals multidimensionals, i poden produir una millor exactitud pel mateix nombre d'avaluacions de la funció que en integracions repetides emprant mètodes unidimensionals. Una classe gran de mètodes útils de Montecarlo són els anomenats algorismes de Cadena de Morkov de Montecarlo, Els quals inclouen l'algorisme de Metropolis-Hastings i el mostreig de Gibbs.

Graelles disperses

Les graelles disperses varen ser desenvolupades inicialment per Smolyak per a la quadratura de funcions de moltes dimensions. El mètode es basa sempre en una mètode de quadratura unidimensional, però fa una més sofisticada combinació de resultats de cada variable.

Connexió amb les equacions diferencials

El problema d'avaluar la integral

$\int _{a}^{b}f(x)\,dx$

es pot reduir a un problema de valor inicial per a una equació diferencial ordinària. Si la integral de més amunt s'escriu com I(b), llavors la funció I satisfà

$I'(x)=f(x),\quad I(a)=0.$

Els mètodes desenvolupats per a resoldre equacions diferencials ordinàries, com per exemple els mètodes de Runge-Kutta, es poden aplicar per a resoldre el problema i per tant es poden emprar per avaluar la integral.

Software per a integració numèrica

La integració numèrica és un dels problemes més intensament estudiats en càlcul numèric.

De les moltes implementacions en programari que hi ha aquí se'n llisten unes quantes.

• QUADPACK (part de SLATEC): descripció , codi font . QUADPACK és una col·lecció d'algorismes, en Fortran, per a integració numèrica basats en la quadratura de Gauss.
• GSL: La llibreria científica GNU (GSL) és una llibreria científica escrita en C que subministra un ample ventall de rutines matemàtiques, com la integració de Montecarlo.
• També es troben algorsimes d'integració numèrica a la Guia de programari matemàtic disponible classe H2.
• ALGLIB és una col·lecció d'algorismes en C# / C++ / Delphi / Visual Basic / etc., per a integració numèrica.

Referències

• Philip J. Davis and Philip Rabinowitz, Methods of Numerical Integration.
• George E. Forsythe, Michael A. Malcolm, and Cleve B. Moler. Computer Methods for Mathematical Computations. Englewood Cliffs, NJ: Prentice-Hall, 1977. (Vegeu Capíto 5.)
• William H. Press, Brian P. Flannery, Saul A. Teukolsky, William T. Vetterling. Numerical Recipes in C. Cambridge, UK: Cambridge University Press, 1988. (Vegeu Capítol 4.)
• Josef Stoer and Roland Bulirsch. Introduction to Numerical Analysis. New York: Springer-Verlag, 1980. (Vegeu Capítol 3.)
• Jon M. Smith Recent Developments in Numerical Integration, J. Dynam. Sys., Measurement and Control 96, Ser. G-1, No. 1, 61-70, Mar. 1974.

Enllaços externs

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Integració numèrica

• Integration: Background, Simulations, etc. al Holistic Numerical Methods Institute