Màquina de Mealy

En la teoria de la computació, una màquina Mealy és una màquina d'estats finits els valors de sortida de la qual estan determinats tant pel seu estat actual com per les entrades actuals. Això contrasta amb una màquina de Moore, els valors de sortida de la qual estan determinats únicament pel seu estat actual. Una màquina Mealy és un transductor d'estat finit determinista: per a cada estat i entrada, és possible com a màxim una transició.

Història

La màquina Mealy porta el nom de George H. Mealy, que va presentar el concepte en un article de 1955, A Method for Synthesizing Sequential Circuits.

Definició formal

Una màquina Mealy és una tupla de 6 $(S,S_{0},\Sigma ,\Lambda ,T,G)$ format pel següent:

• un conjunt finit d’estats $S$
• un estat inicial (també anomenat estat inicial) $S_{0}$ que és un element de $S$
• un conjunt finit anomenat alfabet d'entrada $\Sigma$
• un conjunt finit anomenat alfabet de sortida $\Lambda$
• una funció de transició $T:S\times \Sigma \rightarrow S$ mapejar parells d'un estat i un símbol d'entrada al següent estat corresponent.
• una funció de sortida $G:S\times \Sigma \rightarrow \Lambda$ mapejar parells d'un estat i un símbol d'entrada al símbol de sortida corresponent.

En algunes formulacions, les funcions de transició i de sortida s'uneixen en una única funció $T:S\times \Sigma \rightarrow S\times \Lambda$.

Comparació de màquines Mealy i màquines Moore

1. Les màquines de farina tendeixen a tenir menys estats:
   • Sortides diferents en arcs (n²) en lloc d'estats (n).
2. Les màquines Moore són més segures d'utilitzar:
   • Les sortides canvien a la vora del rellotge (sempre un cicle després).
   • A les màquines Mealy, el canvi d'entrada pot provocar un canvi de sortida tan bon punt es fa la lògica, un gran problema quan dues màquines estan interconnectades; es pot produir una retroalimentació asíncrona si un no té cura.
3. Les màquines de farina reaccionen més ràpidament a les entrades:
   • Reacciona en el mateix cicle: no cal que esperen el rellotge.
   • A les màquines Moore, pot ser que calgui més lògica per descodificar l'estat en sortides: més retards de la porta després de la vora del rellotge.

Diagrama

El diagrama d'estats d'una màquina Mealy associa un valor de sortida a cada aresta de transició, en contrast amb el diagrama d'estats d'una màquina de Moore, que associa un valor de sortida a cada estat.

Quan l'alfabet d'entrada i de sortida són Σ, també es pot associar a un autòmat de Mealy un gràfic dirigit Helix (S × Σ, (x, i) → (T(x, i), G(x, i))). Aquest gràfic té com a vèrtexs les parelles d'estat i lletres, cada node és de grau u fora, i el successor de (x, i) és el següent estat de l'autòmat i la lletra que l'autòmat produeix quan s'instaura x i es llegeix la lletra i. Aquest gràfic és una unió de cicles disjunts si l'autòmat és birreversible.

Exemples

Simple

Diagrama d'estats per a una màquina Mealy senzilla amb una entrada i una sortida. (Per a cada valor d'entrada surt 1 si el valor d'entrada actual és diferent de l'anterior o 0 en cas contrari.)

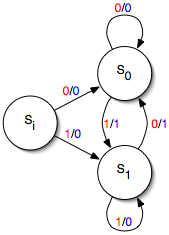
Una màquina Mealy senzilla té una entrada i una sortida. Cada aresta de transició està etiquetada amb el valor de l'entrada (mostrat en vermell) i el valor de la sortida (mostrat en blau). La màquina arrenca en l'estat S_i. (En aquest exemple, la sortida és l’exclusiu o dels dos valors d'entrada més recents; per tant, la màquina implementa un detector de vora, emet un 1 cada vegada que l'entrada gira i un 0 en cas contrari.)

Complex

Les màquines Mealy més complexes poden tenir múltiples entrades i múltiples sortides.

Aplicacions

Les màquines Mealy proporcionen un model matemàtic rudimentari per a màquines de xifratge. Tenint en compte l'alfabet d'entrada i sortida l’alfabet llatí, per exemple, es pot dissenyar una màquina Mealy que donada una cadena de lletres (una seqüència d'entrades) la pugui processar en una cadena xifrada (una seqüència de sortides). Tanmateix, tot i que es podria utilitzar un model de Mealy per descriure l’Enigma, el diagrama d'estat seria massa complex per proporcionar mitjans factibles per dissenyar màquines de xifratge complexes.

Les màquines Moore/Mealy són DFA que també tenen sortida a qualsevol hora del rellotge. Les CPU modernes, ordinadors, telèfons mòbils, rellotges digitals i dispositius/màquines electrònics bàsics tenen algun tipus de màquina d'estats finits per controlar-ho.

Els sistemes de programari senzills, especialment els que es poden representar mitjançant expressions regulars, es poden modelar com a màquines d'estats finits. Hi ha molts sistemes senzills com ara màquines expenedores o electrònica bàsica.

En trobar la intersecció de dues màquines d'estats finits, es poden dissenyar d'una manera molt senzilla sistemes concurrents que intercanvien missatges, per exemple. Per exemple, un semàfor és un sistema que consta de múltiples subsistemes, com els diferents semàfors, que funcionen simultàniament.

Alguns exemples d'aplicacions:

• classificació numèrica
• rellotge amb temporitzador
• expenedor automàtic
• semàfor
• escàner de codi de barres
• bombes de gasolina

Vegeu també

• Màquina de Moore
• Autòmat finit
• Xarxes de Petri
• Teoria de grafs.
• Transductor d'estats finits