Octodecàgon

Octodecàgon
Tipus	polígon
Forma de les cares	aresta (18)
Configuració de vèrtex	segment
Elements
Arestes	18;
Vèrtexs	18
Sèrie
	← heptadecàgon enneadecàgon →
Més informació
MathWorld	Octadecagon

En geometria, un octodecàgon o també conegut com a octadecàgon és un polígon de 18 costats i 18 vèrtexs.

Propietats

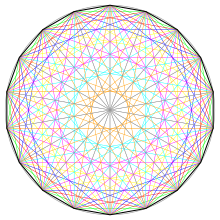
Un octodecàgon té 135 diagonals, resultat que es pot obtenir aplicant l'equació general per determinar el nombre de diagonals d'un polígon, $D=n(n-3)/2$ ; sent el nombre de costats $n=18$ , tenim:

D={\frac {18(18-3)}{2}}=135

La suma de tots els angles interns de qualsevol octodecàgon és: 2880 graus o l'equivalent, $16\pi$ radiants.

Octodecàgon regular

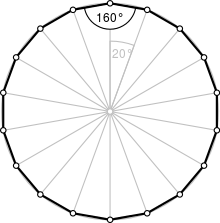
Un octodecàgon regular és el que té tots els seus costats de la mateixa longitud i tots els seus angles interns iguals. Cada angle intern del octodecàgon regular mesura 160º o $8\pi /9$ rad. Cada angle extern del octodecàgon regular mesura 20º o $\pi /9$ rad.

En multiplicar la longitud t d'un costat d'un octodecàgon regular per 18 (el nombre de costats simbolitzats amb la lletra n del polígon) obtindrem la longitud del seu perímetre P.

P=n\cdot t=18\ t

L'àrea A d'un octodecàgon regular amb costat de longitud a s'obté de la següent forma:

A={\frac {18(t^{2})}{4\tan({\frac {\pi }{18}})}}\simeq 25,5208\ t^{2}

on $\pi$ és la constant pi i $tan$ és la funció tangent calculada en radiants.

Si es coneix la longitud de l'apotema a del polígon, una altra alternativa per calcular l'àrea és:

A={\frac {P\cdot a}{2}}={\frac {18(t)\ a}{2}}=9(t\cdot a)

Construcció

Atès que 18=2×3², un octodecàgon regular no pot ser construït usant solament regle i compàs. No obstant això, es pot construir usant el mètode neusis, o una trisecció de l'angle amb un dispositiu trisector.

La següent construcció aproximada és molt similar a la del eneàgon, ja que un octodecàgon pot construir-se com un eneàgontruncat. També és factible amb l'ús exclusiu de regle i compàs.

Reduir la grandària de l'angle AMC (de 60°) mitjançant quatre biseccions consecutives i determinar la tercera part de l'arc MON mitjançant una solució aproximada entre les bisectrius w3 i w4. Per a això, es traça la recta auxiliar g (que passa per O i per N), que serveix per determinar la tercera part de la distància entre O i N mitjançant una altra construcció auxiliar (no representada), que permet determinar el punt Q i després traslladar-ho fins al R. Així, s'obté l'arc circular AMR, que s'aproxima molt notablement a l'angle de 20° buscat. AMR = 19,999999994755615. $\scriptstyle \angle {}$ ..° 360°÷18=20° AMR-20°=-5,244. $\scriptstyle \angle {}$ ..I-9° Exemple per il·lustrar l'error: En una circumferència circumscrita de radi r = 100.000 km, l'error absolut del costat obtingut seria d'aproximadament -9 mm. Consulti's també a wikillibres Càlcul de l'octodecàgon (Berechnung, en alemany) 6.0 JMR equivalent AMR. $\scriptstyle \angle {}$ $\scriptstyle \angle {}$

Simetria

L'octodecàgon regular posseeix simetria diedral Dih18 d'ordre 36. Inclou 5 subgrups de simetria diedrals: Dih9, (Dih₆, Dih3) i (Dih2 Dih1), i 6 simetries cícliques: (Z18, Z9), (Z6, Z3) i (Z2, Z1). Les 15 classes de simetria es materialitzen en 12 tipus de formes de octodecàgon diferents.

John Conway va classificar aquestes simetries usant una lletra i l'ordre de la simetria a continuació. Va assignar la lletra r al grup de simetria de la figura regular; i en el cas dels subgrups va utilitzar la lletra d (de diagonal) per a les figures amb eixos de simetria sol a través dels seus vèrtexs; p per a figures amb eixos de simetria sol a través d'eixos perpendiculars als seus costats; i per a figures amb eixos de simetria tant a través de vèrtexs com a través de centres de costats; i g per a aquelles figures només amb simetria rotacional. Amb a1 s'etiqueten aquelles figures amb absència de simetria. Els tipus de simetries més baixos permeten disposar d'un o més graus de llibertat per definir diferents figures irregulars. Només el subgrup g18 no té graus de llibertat, però pot veure's com un graf dirigit. (Vegeu un exemple en la Teoria de grups de John Conway)

Dissecció

Donald Coxeter va establir que cada zonàgon (un 2m-gon els costats oposats de la qual són paral·lels i d'igual longitud) es pot disseccionar en m(m-1)/2 paral·lelograms.^[1] En particular, això és cert per als polígons regulars amb molts costats, en aquest cas els paral·lelograms són tots rombes. Per l'octodecàgon regular, m=9, i es pot dividir entre 36, formant 4 conjunts de 9 rombes. Aquesta descomposició es basa en una projecció amb forma de polígon de Petrie d'un eneracte, amb 36 de les seves 4608 cares. La llista A006245 enumera el nombre de solucions com 112018190, incloses rotacions de fins a 18 vegades i formes quirals en reflexió.

Dissecció en 36 rombes

Ús

Un triangle equilàter, i un nonàgon i un octodecàgon regulars, poden envoltar completament un punt en el plànol, una de les 17 combinacions diferents de polígons regulars amb aquesta propietat. No obstant això, aquest patró no es pot estendre a un tessel·lat arquimedià del plànol: a causa que el triangle i el nonàgon tenen tots dos un nombre imparell de costats, cap d'ells pot estar completament envoltat per un anell alternant els altres dos tipus de polígon.

L'octodecàgon regular pot tessel·lar el plànol amb espais hexagonals còncaus. I un altre mosaic es pot aconseguir barrejant nonàgons i buits octogonals. El primer mosaic està relacionat amb un tessel·lat hexagonal truncat i el segon amb el tessel·lat hexagonal truncattessel·lat trihexagonal truncat.

240x240px 240x240px

Figures relacionades

Un octodecagrama és un polígon en forma d'estel de 18 costats, representat pel símbol {18/n}. Hi ha dos estels regulars: {18/5} i {18/7}, que utilitzen els mateixos punts, però connecten cada cinquè o setè punt de la figura. També hi ha cinc compostos: {18/2} es redueix a 2{9} o dos eneàgons, {18/3} es redueix a 3{6} o tres hexàgons, {18/4} i {18/8} són reduïts a 2{9/2} i 2{9/4} o dos eneagrames, {18/6} es redueix a 6{3} o 6 triangles equilàters, i finalment {18/9} es redueix a 9{2} com nou dígons.

Compostos i polígons d'estel
n	1	2	3	4	5	6	7	8	9
Forma	Polígon convex	Compostos			Polígon estrellat	Compost	Polígon estrellat	Compost
Imatge	{18/1}= {18}80x80px	{18/2}= 2{9}80x80px	{18/3}= 3{6}80x80px	{18/4}= 2{9/2}80x80px	{18/5}80x80px	{18/6}= 6{3}80x80px	{18/7}80x80px	{18/8}= 2{9/4}80x80px	{18/9}= 9{2}80x80px
Angle interior	160°	140°	120°	100°	80°	60°	40°	20°	0°

Els truncaments més profunds de l'eneàgon regular i els eneagrames poden produir formes de octodecagrames intermedis isogonals (figura isogonal) amb vèrtexs igualment espaiats i dues longituds d'aresta. Altres truncaments formen recobriments dobles: t{9/8} = {18/8} = 2{9/4}, t{9/4} = {18/4} = 2{9/2}, t{9/2} = {18/2} = 2{9}.^[2]

Truncaments transitius de vèrtex del eneàgon i eneagrames
Quasiregular	isogonal	Quasiregular Recubrimiento doble
t{9}={18}81x81px		t{9/8}={18/8}=2{9/4}81x81px
t{9/5}={18/5}81x81px		t{9/4}={18/4}=2{9/2}81x81px
t{9/7}={18/7}81x81px		t{9/2}={18/2}=2{9}81x81px

Polígons de Petrie

L'octodecàgon regular és el polígon de Petrie per a una sèrie de politops de major dimensió, que es mostren en aquests projeccions obliqües sobre el plànol de Coxeter:

Polígons de Petrie octodecagonals
A17	B9		D10		I7
símplex 80x80px	9-ortoplex80x80px	eneracte80x80px	71180x80px	17180x80px	32180x80px	23180x80px	13280x80px

Referències

↑ Harold Scott MacDonald Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum

Bibliografia

Octadecàgon en Googlebooks

Enllaços externs

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Octodecàgon

Weisstein, Eric W., «Octadecagon» a MathWorld (en anglès).

[1] Harold Scott MacDonald Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141

[2] The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum

[1]

[2]