Xarxa neuronal artificial
| No s'ha de confondre amb Circuit neuronal. |

Una xarxa neuronal artificial (XNA), o senzillament xarxa neuronal (XN)[1] és un paradigma d'aprenentatge i processament automàtic inspirat en la forma en què funciona el sistema nerviós dels animals. Es tracta d'un sistema d'interconnexió de neurones en una xarxa que col·labora per produir un estímul de sortida. Aquest conjunt de neurones artificials interconnectades que utilitza un model matemàtic o computacional de processament de dades basat en una aproximació connexionista per a la computació. Dins l'entorn d'intel·ligència artificial és freqüent referir-se a elles com xarxes de neurones o xarxes neuronals.
Els investigadors no es posen d'acord a l'hora de definir què és una xarxa neuronal, però la majoria coincideix a dir que es tracta d'una xarxa d'elements de processament relativament simples en què el funcionament global es troba determinat per les connexions entre els elements de processament i els paràmetres d'aquests. La inspiració original de la tècnica es va extraure de l'estudi de les xarxes bioelèctriques del cervell que estan formades per neurones i per les sinapsis d'aquestes (vegeu xarxa neuronal biològica). En un model de xarxa neuronal, els nodes (també anomenats neurones, neurodes, elements de processament o unitats) estan connectats per formar una xarxa de nodes i, per això, s'anomena xarxa neuronal.
Funcionament
[modifica]Les xarxes neuronals consisteixen en una simulació de les propietats observades en els sistemes neuronals biològics a través de models matemàtics recreats mitjançant mecanismes artificials (com un circuit integrat, un ordinador o un conjunt de vàlvules). L'objectiu és aconseguir que les màquines donin respostes similars a les que és capaç de donar el cervell que es caracteritzen per la seva generalització i la seva robustesa.

Una xarxa neuronal es compon d'unitats anomenades neurones. Cada neurona rep una sèrie d'entrades a través d'interconnexions i emet una sortida. Aquesta sortida ve donada per tres funcions:
- Una funció de propagació (també coneguda com a funció d'excitació), que generalment consisteix en el sumatori de cada entrada multiplicada pel pes del seu interconnexió (valor net). Si el pes és positiu, la connexió s'anomena excitadora , si és negatiu, s'anomena inhibitòria .
- Una funció d'activació, que modifica l'anterior. Pot no existir, en aquest cas, la sortida és la mateixa funció de propagació.
- Una funció de transferència, que s'aplica al valor retornat per la funció d'activació. S'utilitza per a limitar la sortida de la neurona i generalment ve donada per la interpretació que vulguem donar-li a aquestes sortides. Algunes de les més utilitzades són la funció sigmoide (per obtenir valors en l'interval [0,1]) i la tangent hiperbòlica (per obtenir valors en l'interval [-1,1]).
Disseny i programació d'una xarxa neuronal
[modifica]Amb un paradigma convencional de programació a enginyeria del programari, l'objectiu del programador és modelar matemàticament (amb diferents graus de formalisme) el problema en qüestió i posteriorment formular una solució (programa) mitjançant un algorisme codificat que tingui una sèrie de propietats que permetin resoldre aquest problema. En contraposició, l'aproximació basada en les xarxes neuronals part d'un conjunt de dades d'entrada prou significatiu i l'objectiu és aconseguir que la xarxa aprengui automàticament les propietats desitjades. En aquest sentit, el disseny de la xarxa té menys a veure amb qüestions com els fluxos de dades i la detecció de condicions, i més a veure amb qüestions com ara la selecció del model de xarxa, la de les variables a incorporar i el preprocessament de la informació que formarà el conjunt d'entrenament. Així mateix, el procés pel qual els paràmetres de la xarxa s'adeqüen a la resolució de cada problema no es denomina genèricament programació sinó que se sol anomenar entrenament neuronal.
Per exemple en una xarxa que s'aplicarà al diagnòstic d'imatges mèdiques; durant la fase d'entrenament el sistema rep imatges de teixits que se sap són cancerígens i teixits que se sap són sans, així com les respectives classificacions d'aquestes imatges. Si l'entrenament és l'adequat, una vegada conclòs, el sistema podrà rebre imatges de teixits no classificats i obtenir la seva classificació sa /no sa amb un bon grau de seguretat. Les variables d'entrada poden ser des dels punts individuals de cada imatge fins a un vector de característiques de les mateixes que es puguin incorporar al sistema (per exemple, procedència anatòmica del teixit de la imatge o l'edat del pacient a qui se li va extreure la mostra).
Estructura
[modifica]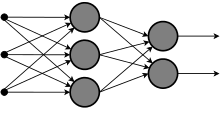
Com el cervell, una xarxa neuronal artificial és un conjunt paral·lel d'unitats de processament petites i simples on les interconnexions constitueixen una gran part de la intel·ligència de la xarxa. No obstant això, les xarxes neuronals artificials són prou diferents del cervell pel que fa a l'estructura. Per exemple, una xarxa neuronal és molt més menuda que el cervell. A més, les unitats utilitzades en una xarxa neuronal són, generalment, molt més simples que les neurones. Tot i això, algunes funcions que semblen exclusives del cervell, com és el cas de l'aprenentatge, s'han reproduït a escala més senzilla en les xarxes neuronals.
La majoria dels científics coincideixen que una xarxa neuronal és molt diferent en termes d'estructura d'un cervell animal. Igual que el cervell, una xarxa neuronal es compon d'un conjunt massivament paral·lel d'unitats de procés molt simples i és en les connexions entre aquestes unitats on resideix la intel·ligència de la xarxa. No obstant això, en termes d'escala, un cervell és molt més gran que qualsevol xarxa neuronal creada fins a l'actualitat, i les neurones artificials també són més simples que la seva contrapartida animal.
Biològicament, un cervell aprèn mitjançant la reorganització de les connexions sinàptiques entre les neurones que el componen. De la mateixa manera, les XNA tenen un gran nombre de processadors virtuals interconnectats que de forma simplificada simulen la funcionalitat de les neurones biològiques. En aquesta simulació, la reorganització de les connexions sinàptiques biològiques es modela mitjançant un mecanisme de pesos , que són ajustats durant la fase d'aprenentatge. En una xarxa neuronal entrenada, el conjunt dels pesos determina el coneixement d'aquesta XNA i té la propietat de resoldre el problema per al qual la xarxa neuronal ha estat entrenada.
D'altra banda, en una xarxa neuronal, a més dels pesos i les connexions, cada neurona té associada una funció matemàtica anomenada funció de transferència. Aquesta funció genera el senyal de sortida de la neurona a partir dels senyals d'entrada. L'entrada de la funció és la suma de tots els senyals d'entrada pel pes associat a la connexió d'entrada del senyal. Alguns exemples d'entrades són la funció graó de Heaviside, la lineal o mixta, la sigmoide i la funció gaussiana, recordant que la funció de transferència és la relació entre el senyal de sortida i l'entrada.
Models
[modifica]En una xarxa neuronal típica, cada node funciona gairebé com una neurona biològica. En una neurona biològica, cada sinapsi d'entrada té un pes associat. Quan el pes de cada sinapsi, multiplicat per la seva entrada, se suma a totes les sinapsis entrants i aquesta suma és major que algun «valor llindar», la neurona es dispara i envia un valor a una altra neurona de la xarxa. El node típic d'una xarxa neuronal intenta emular aquest funcionament. Cada node conté un conjunt de línies d'entrada que són anàlogues a les sinapsis d'entrada d'una neurona biològica. A més, cada node té una «funció d'activació» (coneguda també com a «funció de transferència») que li indica quan ha de disparar-se, semblant a allò que ocorre en una neurona biològica. En la seva forma més senzilla, aquesta funció d'activació pot generar un valor «1» si l'entrada sumada és major que algun valor, però si això no es produeix, generarà un valor «0». No obstant això, les funcions d'activació no sempre són tan senzilles. De fet, per crear xarxes que puguen realitzar una tasca útil, les funcions d'activació quasi sempre han de ser més complexes per a, almenys, alguns dels nodes de la xarxa.
Una xarxa neuronal feedforward, un dels tipus de xarxes neuronals més comuns, està formada per un conjunt de nodes i connexions. Aquests nodes s'organitzen en capes. Generalment, les connexions es formen connectant cadascun dels nodes d'una determinada capa a totes les neurones de la següent capa. D'aquesta manera, tots els nodes d'una determinada capa estan connectats a tots els nodes de la següent.
Normalment, en una xarxa neuronal feedforward hi ha almenys tres capes: una capa d'entrada, una capa oculta i una capa de sortida. La capa d'entrada no processa res, ja que és en aquesta on el vector de dades alimenta la xarxa. Així doncs, la capa d'entrada alimenta la capa oculta i aquesta, al seu torn, alimenta la capa de sortida. El processament real de la xarxa té lloc en els nodes de la capa oculta i de la capa de sortida.
Quan un nombre suficient de neurones estan connectades en capes, la xarxa es pot «entrenar» per realitzar tasques útils usant un algorisme d'entrenament. Les xarxes feedforward, en concret, si estan entrenades apropiadament, són molts útils per realitzar tasques intel·ligents de classificació o d'identificació d'informació desconeguda.
Càlculs
[modifica]La corba sigmoïdal sovint s'utilitza com a funció de transferència perquè aquesta introdueix no-linealitat en els càlculs de la xarxa en delimitar el nivell d'activació de la neurona a un interval [0,1]. La funció sigmoïdal compta amb l'avantatge addicional de tenir una funció derivable molt simple, tal com es requereix per retropropagar els errors a través d'una xarxa neuronal feedforward. A més, poden utilitzar-se altres funcions amb característiques semblants. Majoritàriament, s'usa la funció tanh que delimita les activacions en l'interval [-1, 1] encara que, de vegades, també s'usa una funció lineal piece-wise que simplement talla l'activació en compte de delimitar-la.
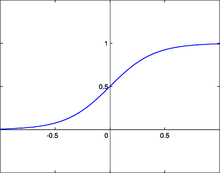
Si no s'introdueix no-linealitat que la delimita o la talla, la xarxa perd gran part del seu poder computacional i es converteix en una senzilla operació de multiplicació de matrius de l'àlgebra lineal.
Altres models de càlculs alternatius de les xarxes neuronals inclouen models amb bucles en què s'utilitzen processos amb retard i models el guanyador s'ho emporta tot on la neurona amb el major valor de càlcul pren un valor 1 i totes les altres neurones prenen el valor 0.
Normalment, els pesos d'una xarxa neuronal s'inicien en uns valors aleatoris baixos. Açò mostra que la xarxa no té cap mena de coneixement; la seua sortida és, bàsicament, una funció aleatòria de l'entrada. A mesura que el procés d'entrenament avança, els pesos de les connexions es modifiquen gradualment segons les regles computacionals específiques de l'algorisme d'aprenentatge que s'utilitza. Finalment, els pesos ideals convergeixen en uns valors que els permeten realitzar un càlcul útil. Es pot dir que, al començament, les xarxes neuronals no tenen cap mena de coneixement i tracten d'obtenir algun tipus de coneixement real, encara que aquest és subsimbòlic.
Avantatges
[modifica]Les xarxes neuronals artificials tenen molts avantatges pel fet que estan basades en l'estructura del sistema nerviós, principalment el cervell.
- Aprenentatge : Les xarxa neuronals tenen l'habilitat d'aprendre mitjançant una etapa que s'anomena etapa d'aprenentatge . Aquesta consisteix a proporcionar a la xarxa neuronal dades com a entrada al seu torn que se li indica quina és la sortida (resposta) esperada.
- Auto organització : Una xarxa neuronal crea la seva pròpia representació de la informació al seu interior, descarregant l'usuari d'això.
- Tolerància a fallades : Atès que una xarxa neuronal emmagatzema la informació de forma redundant, aquesta pot seguir responent de manera acceptable fins i tot si es fa malbé parcialment.
- Flexibilitat : Una xarxa neuronal pot gestionar canvis no importants en la informació d'entrada, com a senyals amb soroll o altres canvis en l'entrada (ex. si la informació d'entrada és la imatge d'un objecte, la resposta corresponent no pateix canvis si la imatge canvia una mica la seva brillantor o l'objecte canvia lleugerament)
- Temps real : L'estructura d'una xarxa neuronal és paral·lela, per la qual cosa si això és implementat amb ordinadors o en dispositius electrònics especials, es poden obtenir respostes en temps real.
- Escalabilitat: poden adaptar-se a qualsevol problema d'una determinada àrea
Aplicacions
[modifica]Utilitat
[modifica]Les xarxes neuronals artificials són especialment útils per a tractar amb dades de nombres reals limitats en què es requereix una sortida amb valor real. D'aquesta manera, les xarxes neuronals realitzaran una classificació per nivells i són capaces d'expressar valors equivalents a no segur. Si la xarxa neuronal s'entrena utilitzant la funció d'error d'entropia creuada (vegeu l'obra Neural Networks for Pattern Recognition, escrita per Christopher M. Bishop) i la sortida de la xarxa és sigmoïdal, aleshores les sortides seran estimacions de la vertadera probabilitat posterior d'una classe.
Aplicacions en la vida real
[modifica]En la vida real, les xarxes neuronals realitzen especialment bé les següents tasques de Classificació i Reconeixement de patrons
Altres tipus de xarxes neuronals i, en especial, les xarxes neuronals recurrents de temps continu s'utilitzen en combinació amb els algorismes genètics (AG) per produir controladors per a robots. El genoma està constituït pels paràmetres de les xarxes i la idoneïtat d'una xarxa és l'adequació del funcionament mostrat pel robot controlat (o sovint per una simulació d'aquest funcionament). No obstant això, també pot utilitzar-se per al reconeixement d'iris.
Classificació
[modifica]Topologia
[modifica]Una primera classificació de les xarxes de neurones artificials que se sol fer és en funció del patró de connexions que presenta. Així es defineixen tres tipus bàsics de xarxes:
- Dos tipus de xarxes de propagació cap endavant o acícliques en què tots els senyals van des de la capa d'entrada cap a la sortida sense existir cicles, ni connexions entre neurones de la mateixa capa.
- Monocapa. Exemples: perceptró, Adaline.
- Multicapa. Exemples: perceptró multicapa.
- Les xarxes recurrents que presenten almenys un cicle tancat d'activació neuronal. Exemples: Elman, Hopfield, màquina de Boltzmann.
Aprenentatge
[modifica]Una segona classificació que se sol fer és en funció del tipus d'aprenentatge que és capaç (si es requereix o no un conjunt d'entrenament supervisat). Per a cada tipus d'aprenentatge trobem diversos models proposats per diferents autors:
- Aprenentatge supervisat: necessiten un conjunt de dades d'entrada prèviament classificat o la resposta objectiu es coneix. Exemples d'aquest tipus de xarxes són: el perceptró simple, la xarxa Adaline, el perceptró multicapa i la memòria associativa bidireccional.
- Aprenentatge no supervisat o autoorganitzat: no necessiten tal conjunt previ. Exemples d'aquest tipus de xarxes són: les memòries associatives, les xarxes de Hopfield, la màquina de Boltzmann i la màquina de Cauchy, les xarxes d'aprenentatge competitiu, les xarxes de Kohonen o mapes autoorganitzats i les xarxes de ressonància adaptativa (ART)
- Xarxes híbrides: són un enfocament mixt en el qual s'utilitza una funció de millora per facilitar la convergència. Un exemple d'aquest últim tipus són les xarxes de base radial.
- Aprenentatge reforçat: se situa a mig camí entre el supervisat i l'autoorganitzat.
Tipus d'entrada
[modifica]Finalment també es poden classificar les XNAs segons siguin capaces de processar informació de diferent tipus a:
- Xarxes analògiques: processen dades d'entrada amb valors continus i, habitualment, acotats. Exemples d'aquest tipus de xarxes són: Hopfield, Kohonen i les xarxes d'aprenentatge competitiu.
- Xarxes discretes: processen dades d'entrada de naturalesa discreta; habitualment valors lògics booleans. Exemples d'aquest segon tipus de xarxes són: les màquines de Boltzmann i Cauchy, i la xarxa discreta de Hopfield.
Tipus de xarxes neuronals
[modifica]Hi ha una sèrie de models que apareixen en la majoria d'estudis acadèmics i la bibliografia especialitzada.
- Perceptró
- Adaline
- Perceptró multicapa
- Memòries associatives
- Màquina de Boltzmann
- Màquina de Cauchy
- Propagació cap enrere Propagació cap enrere (backpropagation)
- Xarxes de Elman
- Xarxes de Hopfield
- Xarxa de contrapropagació
- Xarxes de neurones de base radial
- Xarxes de neurones d'aprenentatge competitiu
- Mapa autoorganitzat (Xarxes de Kohonen)
- Creixement dinàmic de cèl·lules
- Gas neuronal creixent
- Xarxes ART ( Adaptative Resonance Theory )
Perceptró monocapa
[modifica]
El primer tipus de xarxa neuronal és el perceptró monocapa, format per una sola capa de nodes de sortida. Les entrades alimenten directament les sortides a través d'una sèrie de pesos, per això aquest pot considerar-se el tipus més senzill de xarxa feedforward. La suma dels productes dels pesos i de les entrades es calcula en cada node i, si el valor està per sobre un llindar (normalment el 0), la neurona es dispara i pren el valor activat (normalment l'1); si això no ocorre pren el valor desactivat (normalment el -1). A les neurones amb aquest tipus de funció d'activació també se’ls anomena neurones de McCulloch-Pitts o neurones de llindar, descrites als anys 40 per Warren McCulloch i Walter Pitts. En els textos especialitzats, el terme perceptró sol fer referència a les xarxes que consten només d'una d'aquestes unitats.
Es pot crear un perceptró fent servir qualsevol valor de l'estat activat o del desactivat, sempre que el valor del llindar estiga entre els dos*. La major part dels perceptrons tenen sortides d'1 o de -1 amb un llindar de 0. A més, hi ha proves que a aquestes xarxes se’ls pot entrenar més ràpidament que a les xarxes creades per nodes amb valors d'activació i de desactivació diferents. Es pot emprar un algorisme simple d'aprenentatge, generalment anomenat regla delta, per entrenar els perceptrons. Aquest calcula els errors entre la sortida calculada i les dades de sortida de mostra, els empra per crear un reajustament de pesos i implementa així una forma de descens del gradient.
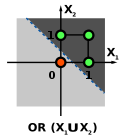
Els perceptrons d'una sola una unitat sols poden aprendre models que són linealment separables. L'any 1969, una famosa monografia titulada Perceptrons, elaborada per Marvin Minsky i Seymour Papert, va mostrar que era impossible que un perceptró monocapa aprenguera la funció XOR. A més, els autors van conjecturar, però de manera equivocada, que ocorreria el mateix amb un perceptró multicapa.
Aplicacions
[modifica]Les característiques de les XNA les fan prou apropiades per a aplicacions en les quals no es disposa a priori d'un model identificable que pugui ser programat, però es disposa d'un conjunt bàsic d'exemples d'entrada (prèviament classificats o no). Així mateix, són altament robustes tant al soroll com a la disfunció d'elements concrets i són fàcilment paral·lelitzades.
Això inclou problemes de classificació i reconeixement de patrons de veu, imatges, senyals, etc. Així mateix s'han utilitzat per trobar patrons de frau econòmic, fer prediccions en el mercat financer, fer prediccions de temps atmosfèric, etc.
També es poden utilitzar quan no hi ha models matemàtics necessaris o algorismes amb complexitat raonable, per exemple la xarxa de Kohonen ha estat aplicada amb un èxit més que raonable al clàssic problema del viatjant (un problema per al qual no es coneix solució algorísmica de complexitat polinòmica).
Un altre tipus especial de xarxes neuronals artificials s'ha aplicat en conjunció amb els algoritmes genètics (AG) per crear controladors per robots. La disciplina que tracta l'evolució de xarxes neuronals mitjançant algoritmes genètics s'anomena robòtica evolutiva. En aquest tipus d'aplicació el genoma de l'AG el constitueixen els paràmetres de la xarxa (topologia, algorisme d'aprenentatge, funcions d'activació, etc.) I l'adequació de la xarxa ve donada per l'adequació del comportament exhibit pel robot controlat (normalment una simulació d'aquest comportament)
Exemples
[modifica]Quake II Neuralbot
[modifica]Un bot és un programa que simula un jugador humà. El Neuralbot és un bot per al joc Quake II que utilitza una xarxa neuronal artificial per decidir el seu comportament i un algorisme genètic per a l'aprenentatge. És molt fàcil provar per veure la seva evolució.[2]
Classificador no esbiaixat de proteïnes
[modifica]És un programa que combina diverses tècniques computacionals amb l'objectiu de classificar famílies de proteïnes. Un possible mètode consisteix a utilitzar mètriques adaptatives com per exemple: mapes autoorganitzats i algoritmes genètics.
El problema de classificació no esbiaixada basada en l'expressió de les proteïnes en Aminoàcids pot reduir-se, conceptualment, al següent:
- La identificació de grups de proteïnes que comparteixin característiques comunes.
- La determinació de les raons estructurals per les quals les proteïnes en qüestió s'agrupen de la manera indicada.
- Evitar la idea d'establir criteris de classificació "esbiaixats", fonamentats en idees preconcebudes per aconseguir la seva classificació. En aquest sentit, hi ha dos assumptes a considerar:
- Com aconseguir la caracterització de les proteïnes de manera no esbiaixada.
- Com aconseguir això sense apel·lar a mesures d'agrupament que, al seu torn, impliquen algun tipus de biaix sobre aquest agrupament.
Les XNA han estat aplicades a un nombre en augment de problemes en la vida real i de considerable complexitat, on el seu major avantatge és en la solució de problemes que són força complexos per a la tecnologia actual, tractant-se de problemes que no tenen una solució algorísmica o amb una solució algorísmica massa complexa per a ser trobada.
En general, pel fet que són semblants a les del cervell humà, les XNA són ben anomenades, ja que són bones per resoldre problemes que l'humà pot resoldre però les computadores no. Aquests problemes inclouen el reconeixement de patrons i la predicció del temps. De totes maneres, l'humà té capacitat per al reconeixement de patrons, però la capacitat de les xarxes neuronals no es veu afectada per la fatiga, condicions de treball, estat emocional, i compensacions.
Es coneixen cinc aplicacions tecnològiques aplicades:
- Reconeixement de textos manuscrits
- Reconeixement de la parla
- Simulació de centrals de producció d'energia
- Detecció d'explosius
- Identificació de blancs de radars
Vegeu també
[modifica]- Conformació de feixos (beamforming)
- Visió artificial
- Reconeixement facial
Referències
[modifica]- ↑ «xarxa neuronal». Cercaterm. TERMCAT, Centre de Terminologia. [Consulta: 31 octubre 2023].
- ↑ http://homepages.paradise.net.nz/nickamy/neuralbot/index.html Arxivat 2006-04-11 a Wayback Machine.