Transformació isomètrica

Les transformacions isomètriques són transformacions de figures en el pla que es realitzen sense variar les dimensions ni l'àrea d'aquestes, la figura inicial i la final són semblants, i geomètricament congruents.
La paraula isometria té el seu origen en el grec iso (igual o mateix) i metria (mesurar), una definició propera seria: mateixa mesura . Hi ha tres tipus d' isometria : translació, simetria i rotació.
Translació[modifica]
La translació és una isometria que realitza un canvi de posició, és el canvi de lloc, determinada per un vector.
 |
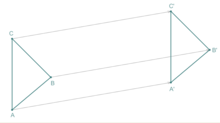 |
Es diu translació de vector va la isometria que a cada punt m del pla li fa correspondre un punt 'm' del mateix pla tal que mm' és igual a v.
Les translacions estan marcades per tres elements: La direcció, si és horitzontal, vertical un obliqua. El sentit, dreta, esquerra, amunt i avall. I la magnitud del desplaçament que es refereix a quant es va desplaçar la figura en una unitat de medida.s Això fa referència exclusivament a les translacions isomètriques
Simetria[modifica]
Simetria és la correspondència exacta en la disposició regular de les parts o punts d'un cos o figura amb relació a un punt (centre), una recta (eix) o un pla. Es denominen: central, axial i especular o bilateral.
Simetria central[modifica]
La simetria central, en geometria, és una transformació en la qual a cada punt se li associa un altre punt, que ha de complir les següents condicions:
a) El punt i la seva imatge estan a igual distància d'un punt anomenat centre de simetria.
b) El punt, la seva imatge i el centre de simetria pertanyen a una mateixa recta.
 |
 |
Segons aquestes definicions, amb una simetria central s'obté la mateixa figura amb una rotació de 180 graus.
Simetria axial[modifica]
La simetria axial, en geometria, és una transformació respecte d'un eix de simetria , en la qual, a cada punt d'una figura s'associa a un altre punt anomenat imatge, que compleix amb les següents condicions:
a) La distància d'un punt i la seva imatge a l'eix de simetria, és la mateixa.
b) El segment que uneix un punt amb la seva imatge, és perpendicular a l'eix de simetria.
 |
 |
A la simetria axial es conserven les distàncies però no el sentit dels angles. L'eix de simetria és la mediatriu del segment AA '.
Composició de simetries[modifica]
Si s'aplica la mateixa simetria dues vegades, s'obté una identitat .
Si s'apliquen dues simetries respecte d'eixos paral·lels, s'obté una translació el desplaçament és el doble de la distància entre aquests eixos.
Si s'apliquen dues simetries respecte d'eixos que es tallen a O, s'obté gir amb centre a O, l'angle és el doble del que formen aquests eixos.
Rotació[modifica]
Una rotació, en geometria, és un moviment de canvi d'orientació d'un cos, de manera que, donat un punt qualsevol seu, aquest roman a una distància constant d'un punt fix, i té les següents característiques:
- Un punt anomenat centre de rotació.
- Un angle
- Un sentit de rotació.
aquestes transformacions poden ser positives o negatives depenent del sentit de gir. Per al primer cas ha de ser un gir en sentit contrari a les agulles del rellotge, i serà negatiu el gir quan sigui en sentit de les agulles.
 |
Enllaços externs[modifica]
- Simetries, en Descartes.cnice.mec.es[Enllaç no actiu]
- Simetries, en isftic.mepsyd.es Arxivat 2010-03-11 a Wayback Machine.
- Funció simètrica, en Descartes.cnice.mec.es
