Moviment

El moviment és un desplaçament en què es canvia de posició (desplaçament) o d'orientació (rotació). Un cos en moviment, si es desplaça, pot descriure una trajectòria.
La part de la física que s'encarrega d'estudiar el moviment és la mecànica. La mecànica es divideix en cinemàtica, quan no es tenen en compte les forces externes, i dinàmica, quan sí que entren en l'estudi. D'altra banda, la cinesiologia estudia el moviment del cos humà, que hom percep per mitjà de la cinestèsia.
Introducció[modifica]
Un sistema físic real es caracteritza per, almenys, tres propietats importants:
- Tenir una posició a l'espai-temps.
- Tenir un estat físic definit subjecte a evolució temporal.
- Poder-se associar una magnitud física anomenada energia.
El moviment es refereix al canvi al llarg del temps d'una propietat a l'espai, com pot ser la ubicació, l'orientació, la forma geomètrica o la mida, tal com es mesura per un observador físic. Una mica més generalment el canvi de propietat a l'espai es pot veure influït per les propietats internes d'un cos o sistema físic, o fins i tot l'estudi del moviment en tota la generalitat porta a considerar el canvi d'aquest estat físic.
La descripció del moviment dels cossos físics sense considerar les causes que l'originen s'anomena cinemàtica (del grec κινεω, kineo, moviment) (que només s'ocuparia de les propietats 1 i 2 anteriors). Es limita a l'estudi de la trajectòria i el desplaçament en funció d'elements geomètrics que evolucionen amb el temps. Aquesta disciplina pretén descriure la manera com es mou un determinat cos. La física clàssica va néixer estudiant la cinemàtica de cossos rígids.
Posteriorment l'estudi de l'evolució en el temps d'un sistema físic en relació amb les causes que provoquen o conserven el moviment va portar al desenvolupament de la dinàmica. Els principis dinàmics més importants són la inèrcia, la quantitat de moviment, la força i l'energia mecànica.
La integració de la cinemàtica i la dinàmica desenvolupa la disciplina general anomenada mecànica (Grec Μηχανική i de llatí mechanica o 'art de construir màquines') que és la branca de la física que estudia i analitza el moviment i repòs dels cossos. La mecànica teòrica va ser durant els segles XVII, XVIII i principis del segle xix, la disciplina de la física que va aconseguir més abstracció matemàtica i va ser una font de millora del coneixement científic del món. La mecànica aplicada està usualment relacionada amb l'enginyeria. Ambdós punts de vista es justifiquen parcialment ja que, si bé la mecànica és la base per a la majoria de les ciències de l'enginyeria clàssica, no té un caràcter tan empíric com aquestes i, en canvi, pel seu rigor i raonament deductiu, s'assembla més a la matemàtica. Durant el segle xx l'aparició de nous fets físics, tant la consideració de cossos físics movent-se a velocitats properes a la velocitat de la llum com el moviment de les partícules subatòmiques, van portar a la formulació de teories més abstractes com la mecànica relativista i la mecànica quàntica que seguien interessant-se per l'evolució en el temps dels sistemes físics, encara que d'una manera més abstracta i general del que havia fet la mecànica clàssica, l'objectiu de la qual era bàsicament quantificar el canvi de posició a l'espai de les partícules al llarg del temps i els agents responsables d'aquests canvis.
Equacions del moviment[modifica]
Les equacions d'un moviment descriuen el moviment d'una partícula, cos o part d'aquest respecte a una referència i en una base algebraica.
Alguns moviments en una dimensió[modifica]
Per a cada dimensió espacial, alguns dels casos particulars més simples de moviments en una partícula (un punt) són:
- Moviment rectilini uniforme, sense cap tipus d'acceleració, sense cap gir (canvis de direcció, corbes) ni rotacions
- Moviment rectilini uniformement accelerat, només acceleració al desplaçament, i aquesta és constant, sense cap gir (cap canvi de direcció) ni rotacions
- Moviment harmònic simple, la velocitat pot ser positiva (desplaçament "endavant") o negativa ("endarrere"), només acceleració al desplaçament, sense cap gir.
Alguns moviments en dues dimensions[modifica]
Relació entre posició, velocitat i acceleració[modifica]
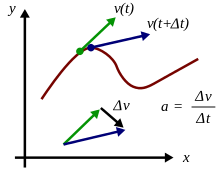

Per a cada dimensió espacial, la velocitat (lineal i angular) instantània d'un punt és la derivada de l'equació que descriu la posició (trajectòria) respecte al temps, en aquell instant de temps, i l'acceleració (lineal i angular) instantània és la derivada de l'equació que descriu la velocitat respecte al temps, en el mateix instant de temps.
De la mateixa manera, l'equació que descriu la velocitat és la integral de l'equació que descriu l'acceleració, i la de la posició la integral de la de la velocitat.
Si és la posició en funció del temps:
Percepció del moviment[modifica]
La percepció del moviment és la resposta del sistema visual en funció del temps. Tenim dos tipus de respostes segons l'estat de l'estímul: la resposta lenta i la resposta ràpida.
Les cèl·lules del nervi òptic[modifica]
Al 1974 es van descobrir dos tipus de cèl·lules en el nervi òptic que responien de manera diferent als estímuls lluminosos. Aquestes eren dos tipus de respostes del sistema visual davant la permanència o la transitorietat dels estímuls.
Resposta lenta[modifica]

És la resposta que el nostre sistema visual ofereix als estats d'estimulació permanents. Aquesta resposta comporta la retenció de les imatges una fracció de segon després que el subjecte deixi de tenirles davant; això permet que veguem la realitat com una seqüència d'imatges que el cervell interpreta com única, mòbil i contínua. Aquest efecte anomenat persistència retiniana va descobrir-se gràcies a les observacions de Peter Mark Roget i de la posterior demostració de Joseph Plateau mitjançant el Fenaquistoscopi: aparell òptic que permetia reproduir el moviment d'una imatge. La percepció retiniana es dona a causa del temps (entre 30 i 200 mil·lèsimes de segon) que tarda la retina en enviar la senyal nerviosa al cervell i el que tarda aquest en processar la informació. Aquest tipus de resposta s'entén com un conjunt d'efectes d'excitació i d'integració, els quals fan que diversos fenòmens que succeeixen simultàniament s'integrin en una sola percepció.
Des de principis del segle xix, s'ha emprat la persistència retiniana per explicar que la projecció seqüencial d'imatges estàtiques lleugerament diferents podria donar la sensació de moviment; com és en el cas del cinema. Malgrat que moltes fonts segueixin considerant aquesta teoria com a vàlida, s'ha demostrat que la persistència retiniana per si sola és incapaç d'explicar la complexa percepció del moviment. Si la consideréssim com un fenomen aïllat, el que percebríem seria una superposició d'imatges de forma caòtica que persisteixen un cert temps les unes sobre les altres. En el cinema, per exemple, no es va donar una sensació de moviment real fins que no es va intercalar un temps determinat de negre entre dues imatges fixes. Aquí neix una nova teoria que defensa precisament que tan sols anul·lant l'efecte de la persistència retiniana, el nostre cervell pot interpretar la successió d'imatges estàtiques com un moviment. Aquesta espècie de fons negre en el cinema podríem considerar-lo semblant al temps que el nostre cervell necessita per a processar la informació de la retina. Aquesta teoria però ha quedat qüestionada en l'actualitat, ja que sembla que no sigui tant senzill.[1]
Resposta ràpida[modifica]
És la resposta que el nostre sistema visual ofereix als estats d'estimulació transitoris. Hi han dos tipus d'efectes que responen a la percepció d'imatges en moviment: el centelleig i l'emmascarament visual.
El centelleig es dona quan l'ull observa una llum d'una determinada freqüència que s'encén i s'apaga periòdicament. Segons la freqüència que tarda aquesta llum en tornar-se a encendre, podem percebre la seqüència com una imatge de caràcter continu; és a dir, com si la llum estigues contínuament encesa. És un efecte semblant al mirar una roda en moviment, ja que la percebem com un subjecte estàtic. La freqüència a la que ha d'estar sotmesa la llum per tal de produir aquest efecte depèn de la seva intensitat, ja que pot ser de només 10 Hz per a intensitats petites o arribar a 1000 Hz per a intensitats més grans. Aquest efecte el podem relacionar directament amb les pampallugues del cinema primitiu. Per combatre aquest efecte, van haver d'introduir làmpades més lluminoses, làmpada d'arc voltaic, i van haver de modificar l'antiga freqüència que s'utilitzava, 24 imatges per segon. La dificultat que suposava augmentar la velocitat dels fotogrames va resoldre's amb la decisió de la doble projecció de cada un d'ells. Així, la freqüència de projecció va augmentar a 48 imatges per segon, tan sols fent que l'obturador talli el flux lluminós dues vegades per fotograma.
Quan dos estímuls lluminosos es troben molt propers en el temps es produeix un efecte d'emmascarament visual, on el segon pertorba la percepció del primer; és a dir, actua com a màscara. Aquest efecte es veu de manera molt clara en el món del cinema. Si entre dos fotogrames hi interposem un fotograma blanc s'anul·larà la sensació de moviment; en canvi, si en comptes d'interposar un fotograma blanc ho fem amb un de negre, la imatge no es veurà distorsionada gràcies a l'absència d'estímuls lluminosos que provoquin un emmascarament. Per tant, podrem percebre la seqüència en moviment. Aquí, retrobem de nou l'efecte de la persistència retiniana, ja que moltes teories (una de les quals hem esmentat anteriorment) responsabilitzen l'emmascarament visual d'anul·lar aquest fenomen.
A partir d'aquests coneixements sobre les respostes d'aquestes dues cèl·lules especialitzades, entenem la percepció del moviment a partir de dues parts independents l'una de l'altra. Una d'elles, són unes cèl·lules cerebrals que actuen com a detectors de moviment, ja que reaccionen quan un estímul s'activa successivament a gran velocitat. Per altra banda, tenim una sèrie de mecanismes correctors que elideixen el moviment dels nostres ulls, fent que no els interpretem pròpiament com a moviment. Per fer-ho, aquests mecanismes comparen contínuament la informació eferent, del cervell als òrgans sensitivo-motors, i la informació aferent, dels òrgans sensitivo-motors al cervell. La percepció del moviment també està vinculat a altres factors externs com ara les dimensions de l'objecte, la il·luminació, el contrast i l'entorn.[2]
Moviment aparent[modifica]
El moviment aparent és un fenomen perceptiu que fa que percebem com a moviment un estímul estàtic. Per tant, el moviment aparent no és res més que una il·lusió perceptiva que no requereix un moviment real per distingir una sensació de moviment.[3] Ha quedat comprovat gràcies als diversos aparells simuladors de moviment i a altres experiències al laboratori que el moviment pot simular-se a partir d'imatges estàtiques. A continuació, s'exposen els diversos experiments que s'han dut a terme per a controlar les diferents variants en la percepció d'aquest tipus de moviment.
Donem el cas que se'ns mostrin dos punts lluminosos propers en l'espai que s'encenguin i s'apaguin periòdicament. Segons l'interval que separi aquesta interrupció, podrem percebre l'escena com si fos un únic punt que es desplaça per l'espai. És el que anomenem efecte Beta.
Per contra, l'efecte Alfa es dona quan se'ns mostren dos punts lluminosos de mida diferent en el mateix espai (superposats). De nou, segons el temps que tardin en encendre's de nou, podem percebre l'encesa com un únic moviment d'expansió.[4]
El conjunt d'ambdós efectes s'anomenen efecte fi que consisteix en una sèrie de processos post-retinians que permeten que interpretem imatges fixes com a moviment sotmetent-les a una velocitat molt alta.[5] Els psicòlegs de la Gesalt estableixen que percebem moviment malgrat que cap estímul estigui movent-se realment. Per tant, la nostra percepció no depèn només de l'estímul sino de l'experiència total del moviment i la reorganització que en fem.[6] Gràcies a aquest efecte entenem que l'atribut més important per transmetre moviment, per sobre del color i la forma, és la lluminositat.
Moviment en el cinema[modifica]
La projecció cinematogràfica consisteix en separar un seguit d'imatges fixes per moments de foscor d'una certa freqüència. Un cop escollim la freqüència que eviti el centelleig (fenomen propi en els primers anys del cinema) i, per tant, evitem la sensació de fragmentació de la seqüència, obtindrem una sensació de llum contínua i una consecutivitat.
La càmera cinematogràfica té en compte la persistència retiniana per a obtenir un nombre d'imatges estàtiques per segon que sigui suficient perquè l'espectador les percebi com a moviment i no com una successió. A l'inici la cadència era de tan sols 16 fotogrames per segon, la qual cosa feia que en el cinema primitiu hi trobéssim franges i interrupcions. Més tard, va anar perfeccionant-se i va augmentar fins als 24 fotogrames per segon, obtenint així una major fluïdesa i un moviment més net.[7]
Com que la seqüència d'imatges fixes que configuren un moviment en el cinema són bastant semblants, els mecanismes perceptius que hi intervenen són els mateixos que per la percepció de moviment real. Segons aquesta teoria, fisiològicament no podríem distingir el cinema de la realitat.
Vegeu també[modifica]
- Moviment relatiu
- Quantitat de moviment
- Grau de llibertat del moviment
- Centre instantani de rotació
- Energia cinètica
- Vibracions mecàniques
- Percussió
Referències[modifica]
- ↑ Reserved, Enrique Martínez-Salanova Sánchez - All Rights. «Los antecedentes del cine. El pre-cine». [Consulta: 3 desembre 2018].
- ↑ «La percepció del moviment». [Consulta: 3 desembre 2018].
- ↑ «moviment aparent». [Consulta: 3 desembre 2018].
- ↑ «Percepción del movimiento aparente» (en castellà). [Consulta: 12 desembre 2018].
- ↑ «Massmedia - Lecture notes 1 - 20254: Massmedia y Lenguajes Audiovisuales - StuDocu». [Consulta: 11 desembre 2018].
- ↑ Fem psicologia. Una orientació per als futurs psicòlegs. Edicions Universitat Barcelona, 2000. ISBN 9788483382042.
- ↑ «7.1 La sensació de moviment - Cultura Audiovisual 2n Batxillerat». [Consulta: 11 desembre 2018].[Enllaç no actiu]





