Els polinomis d'Hermite són un exemple de polinomis ortogonals que troben el seu principal àmbit d'aplicacions en mecànica quàntica, sobretot en l'estudi de l'oscil·lador harmònic unidimensional. Són nomenats així en honor de Charles Hermite.
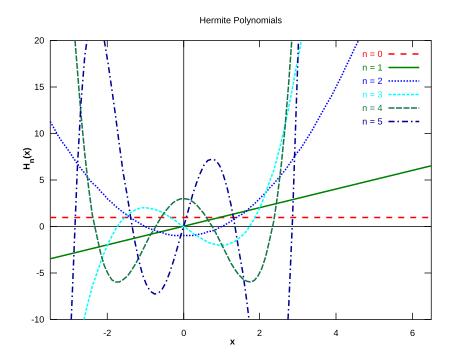 Els cinc primers polinomis d'Hermite (probabilístics').
Els cinc primers polinomis d'Hermite (probabilístics').
Els polinomis d'Hermite:

es defineixen com els polinomis d'Hermite probabilístics o, de vegades, com els polinomis d'Hermite físics:

Aquestes dues definicions no són exactament equivalents, una és un reescalat trivial de l'altra:
 .
.
Els polinomis físics poden expressar-se com:

 és un polinomi de grau n, amb n = 0, 1, 2, 3,... Aquests polinomis són ortogonals respecte de la funció pes (mesura):
és un polinomi de grau n, amb n = 0, 1, 2, 3,... Aquests polinomis són ortogonals respecte de la funció pes (mesura):
 (probabilista)
(probabilista)
o
 (física)
(física)
és a dir,

 (probabilista)
(probabilista)
o
 (física)
(física)
on δ ij és la delta de Kronecker, que val la unitat quan n = m i zero en un altre cas. Els polinomis probabilístics són ortogonals respecte de la funció de densitat de probabilitat normal.
Funció generadora[modifica]

Fórmules de recurrència[modifica]
Els polinomis d'Hermite (en la seva forma "física") satisfan les següents relacions de recurrència:


Descomposició en sèrie de funcions[modifica]
Tota funció f contínua pot expressar-se com sèrie infinita en termes de polinomis d'Hermite:

On les constants de l'anterior sèrie venen donades per:

Altres resultats[modifica]



Equació diferencial d'Hermite[modifica]
Els polinomis d'Hermite són solucions de l'equació diferencial d'Hermite:[1]

que en forma canònica es pot escriure com:

- ↑ Spiegel & Abellanas, 1992, p.158.
- Spiegel, Murray R.; Abellanas, Lorenzo. McGraw-Hill. Fórmules i taules de matemàtica aplicada, 1992. ISBN 84-7615-197-7.





















