Planímetre

Un planímetre és un instrument de mesura utilitzat per al càlcul d'una àrea irregular. Aquest model s'obté basant-se en la teoria de la integral de línia o de recorregut. Per als casos en què es necessita calcular superfícies irregulars o en perspectiva, com mapes o taques, la geometria clàssica o fins i tot la geometria analítica no són suficients i no presten gaire utilitat. Per això és necessari recórrer a una eina de mesura específica per aquesta finalitat, el planímetre és una fàcil alternativa. El matemàtic suís Jacob Amsler-Laffon va construir el primer planímetre modern el 1854,[1] tot i que la idea ja havia estat estudiada el 1814 per Johann Martin Hermann. Molts dels desenvolupaments posteriors, incloent les versions electròniques, segueixen el disseny d'Amsler-Laffon.
Model i esquema d'utilització[modifica]

Es té un origen O, dues longituds constants conegudes R i L, i els angles variables que formen respectivament amb l'horitzontal
Per poder calcular l'àrea A de la secció irregular, segons la teoria del càlcul, s'empra una integral de línia en sentit contrari a les agulles del rellotge (per un resultat positiu).
Però el vector r, no és fàcil d'implementar en la vida real, ja que té una magnitud i un angle variables. Per simplificar la implementació del vector r, es recorre a la suma de dos vectors de mòdul constant, amb dos angles variables, els quals són senzills de mesurar.
Principi de funcionament[modifica]
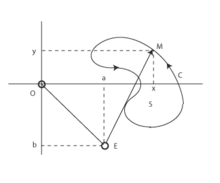

El principi de funcionament de planímetre es basa en el teorema de Green. Aplicant el teorema de Green
a
Q ue pot ser reescrit com
per facilitar la identificació dels termes corresponents) tenim:
El costat dret d'aquesta equació és proporcional a la superfície delimitada pel perímetre. El costat esquerre és igual a
L'integrant té la forma d'un producte escalar, el que significa que la integral és la integral de la projecció de (dx, dy) sobre (-y, x). El vector (-x, y) és perpendicular al (x, y).
Conclusions[modifica]
L'equació és fàcilment programable en molts llenguatges de programació d'alt nivell (PASCAL, C, FORTRAN, etc.), ja que només es necessita el mostreig dels dos angles. Els angles es poden mesurar manualment i entrar les dades registrades al programa del planímetre.
Referències[modifica]
- ↑ Ulmann, Bernd. Analog Computing (en (anglès)). Múnic: Oldenburg, 2013, p. 9-10. ISBN 978-3-486-72897-2.
Vegeu també[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Planímetre |




![{\displaystyle \int _{S}\left({\frac {\partial \left[x\right]}{\partial x}}-{\frac {\partial \left[-y\right]}{\partial y}}\right)\,dx\,dy=\int _{S}2\,dA}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e70a2274271ed77388662f2492553c89344b8c2)
