Teorema xinès del residu
El teorema xinès del residu és un resultat d'aritmètica modular que tracta de la resolució de sistemes de congruències. Aquest resultat establert inicialment sobre Z/nZ es generalitza en teoria d'anells. Aquest teorema es fa servir en la teoria de nombres.
Història[modifica]

La forma original del teorema, continguda en un llibre del matemàtic xinès Qin Jiushao publicat el 1247, és un resultat en relació amb els sistemes de congruències (vegeu aritmètica modular). Però es troba rastre d'un problema anàleg al llibre de Sun Zi, el Sunzi suanjing datant del segle iii:
- Quants soldats té l'exèrcit de Han Xing si, formats en 3 columnes, queden dos soldats, formats en 5 columnes, queden tres soldats i, formats en 7 columnes, queden dos soldats?
Es pot pensar que els Xinesos, a base de fer càlculs astronòmics poguessin estar interessats en concordances de calendari i que hagin arribat a interessar-se per preguntes del tipus:
- A quants dies del solstici d'hivern caurà la lluna plena?
Si la qüestió es fa mentre que queden 6 dies abans del solstici d'hivern i 3 dies abans de la lluna plena, la pregunta es tradueix en:
- Existeix un enter x tal que el residu de la divisió de x entre 365 dona 6 i el residu de la divisió de x entre 28 dona 3?
La resolució proposada per Sun Zi per al problema dels soldats és la següent:
- Multiplica el residu de la divisió entre 3, és a dir 2, per 70, afegeix-li el producte del residu de la divisió entre 5, és a dir 3, per 21 després afegeix el producte del residu de la divisió entre 7, és a dir 2 per 15. Mentre el nombre sigui més gran que 105, resta-li 105.
Però la solució no explica més que imperfectament el mètode emprat.
Finalment, seria una llàstima no presentar aquest problema en relació amb pirates i un tresor, exemple citat molt freqüentment per il·lustrar el teorema dels residus xinesos:
- Una banda de 17 pirates posseeix un tresor constituït de peces d'or d'igual valor. Projecten de partir-se-les a parts iguales, i de donar-ne la resta al cuiner xinès. Aquest rebria llavors 3 peces. Però els pirates es barallen, i sis d'ells moren. Un nou repartiment donaria al cuiner 4 peces. En un naufragi ulterior, sols se salven, el tresor, sis pirates i el cuiner, i el repartiment donaria llavors 5 peces d'or a aquest últim. Quina és la fortuna mínima que pot esperar el cuiner si decideix enverinar la resta dels pirates?
L'aritmètica modular ha tornat a subministrar eines que fan aquest tipus de problema més fàcil de resoldre.
Sistema de congruències d'enters[modifica]
Teorema[modifica]
Siguin , ..., enters primers entre ells dos a dos (és a dir Mcd (ni, nj) = 1 sempre que i ≠ j). Llavors per a tots els enters , ..., , existeix un enter x, únic mòdul i tal que
Una solució x es pot trobar com segueix:
Per a cada i, els enters i són primers entre ells, i segons el teorema de Bachet-Bézout, es poden trobar enters i tals que . Si es posa , llavors es té
i
- per j ≠ i.
Una solució d'aquest sistema de congruències és per tant
De forma més general, totes les solucions x d'aquest sistema són congruents mòdul el producte n
Exemple[modifica]
El problema dels soldats es redueix a
llavors s'obté
- i , o per tant
- i , o per tant
- i , o per tant
una solució per a x és llavors
i les solucions són tots els enters congruents amb 233 mòdul 105, és a dir a 23 mòdul 105.
Generalització a nombres no primers entre ells[modifica]
A vegades, els sistemes de congruències poden ser resolts encara que els ni no siguin primers entre ells dos a dos. Existeix una solució x si i només si per a tot i i j. Totes les solucions x són congruents mòdul el mcm dels ni.
Exemple: resoldre el sistema
equival a resoldre el sistema
equival al sistema
- et , or ja que
- et , or ja que
Una solució és per tant o qualsevol altre nombre congruent amb 11 mòdul 12
El mètode de les substitucions successives sovint pot donar les solucions dels sistemes de congruències, fins i tot quan els mòduls no són primers entre ells dos a dos.
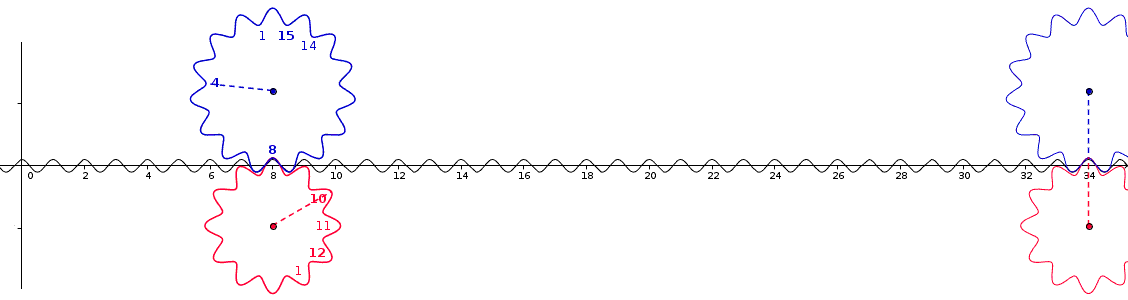
Interpretació mecànica[modifica]
La resolució del sistema següent:
d'incògnita x passa pel càlcul del mcm de a i b.
Aquest problema matemàtic és una modelització d'un problema d'engranatges: una roda dentada de a dents engrana amb una cremallera horitzontal. Quantes dents han de passar perquè la seva r-èsima dent coincideixi amb la s-èsima dent d'una altra roda dentada que engrana amb la mateixa cremallera i que té b dents?
El mcm dels dos nombres a i b és el que permet comprendre el comportament periòdic d'aquest sistema: és el nombre de dents que separa dos contactes del mateix parell de dents (són les dents de la cremallera que són congruents al mateix temps amb les dentes de les dues rodes dentades). Es pot doncs trobar la solució, si n'hi ha una, en l'interval [1,mcm(a,b)]. Hi ha una solució si el mcd (a, b) divideix r - s.
m.c.m.(12,15)=60 . la solució x ∈ [1,60] : x = 34 .
Es pot entendre de manera senzilla per què el càlcul sobre rodes dentades fa intervenir aritmètica modular, fixant-se que el conjunt de les dents d'una roda que en té n es pot parametritzar pel conjunt de les arrels n-èsimes de la unitat, que té una estructura de grup isomorf de manera natural amb la de Z/nZ.
Resultat per als anells[modifica]
Als anells Z/nZ[modifica]
El teorema xinès té una versió més abstracta: si n1..., nk són dos a dos primers entre ells llavors, notant n el producte de ni, l'aplicació
és un isomorfisme d'anells.
Per demostrar-ho cal fixar-se primer en què els dos conjunts i tenen el mateix nombre d'elements. Com que és un morfisme d'anells, n'hi ha prou amb veure que és injectiu per deduir-ne que és un isomorfisme. Per veure això n'hi ha prou amb mostrar que el nucli es redueix a 0 : si per a , és a dir si és un múltiple de cada , llavors , és a dir és un múltiiple del producte . Això resulta de la hipòtesi que els són primers dos a dos.
En el cas on els ni no són primers entre ells, n és el seu mcm i el morfisme de més amunt no és que injectiu. Existeix una solució al problema inicial si i només si les dades són a la imatge, és a dir que el mcd de ni i nj divideix per a tota parella i,j.
En un anell principal[modifica]
Per a un anell principal R, el teorema xinès del residu pren la forma següent: Si u1, ..., uk són els elements de R que són primers entre ells dos a dos, i u designa el producte u1...uk, llavors l'anell R/uR i l'anell producte R/u1R x ... x R/ukR són isomorfs per l'isomorfisme
tal que
L'isomorfisme invers es pot construir així. Per a cada i, els elements ui i u/ui són primers entre ells, i per tant, existeixen elements r i s a R amb
Fixant ei = s u/ui. Es té:
per a j ≠ i.
Llavors la inversa és la transformació
tal que
Resultat per als anells generals[modifica]
Una de les formes més generals del teorema xinès del residu es pot formular en termes d'anell i d'ideal (per l'esquerra o per la dreta). Si R és un anell i I1, ..., Ik ideals de R que són primers entre ells dos a dos (això vol dir que Ii + Ij = R quan i ≠ j), llavors l'ideal producte I d'aquests ideals és igual a la seva intersecció, i l'anell quocient R/I és isomorf a l'anell producte R/I1 x R/I₂ x ... x R/Ik via l'isomorfisme de en que a li associa .
Exemple dels polinomis[modifica]
Un cas freqüent que il·lustra el paràgraf precedent es dona per l'anell dels polinomis. Si x0, x1, ..., xn són n+1 elements de diferents dos a dos, llavors es pot prendre Ui = X - xi. Els polinomis Ui són primers entre ells dos a dos, i el teorema xinès del residu s'aplica. Es prenen per Ei els polinomis d'interpolació de Lagrange, definits per: .
Per a j diferent de i, Ei és divisible entre Uj, de manera que Ei ≡ 0 mòdul Uj. D'altra banda, mòdul Ui, X ≡ xi, de manera que Ei ≡ 1 mòdul Ui.
Dir que un polinomi P és tal que P(xi) = yi per a tot i, és equivalent a dir que P ≡ yi mòdul Ui. Tal polinomi P ve donat per . Cosa que es pot verificar per càlcul directe.
Aplicacions[modifica]
El teorema xinès del residu es fa servir en particular en l'algoritme RSA en criptografia.
Permet representar grans nombres enters com n-tuples de residus de divisions euclidianes. Sota aquesta forma, operacions com l'addició o la multiplicació es poden fer en paral·lel en temps constant. En canvi, la comparació o la divisió no són trivials.
Enllaços externs[modifica]
- (anglès) Teorema xinés del residu














































![{\displaystyle \left\{{\begin{array}{l}x\equiv 4[15]\\x\equiv 10[12]\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31d3f5f3c9ecf137758c680e923cf686bd747ddf)
![{\displaystyle {\begin{matrix}\phi :&\mathbb {Z} /n\mathbb {Z} &\longrightarrow &\mathbb {Z} /n_{1}\mathbb {Z} \times \cdots \times \mathbb {Z} /n_{k}\mathbb {Z} \\&\alpha &\longmapsto &(\alpha [n_{1}],\dots ,\alpha [n_{k}])\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7293f64d02c51ea0fa1c481face940178499b0b8)



![{\displaystyle \alpha =0[n_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7d8f1063f4526889342c2b99f107824818cf27e)



![{\displaystyle \alpha =0[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cee1597d9f29148ee86c523a0a7d57147c3fb05d)












![{\displaystyle \mathbb {K} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a049dae45f6e8d0399188d2d3934b7c0cded5bae)


