Base de Gröbner

En matemàtiques, i més específicament en computació algebraica, geometria algebraica computacional, i àlgebra commutativa computacional, una base de Gröbner (o base estàndard) és un cas particular de conjunt generador d'un ideal en un anell de polinomis sobre un cos K[x₁, ..., x_n]. El fet de disposar d'una base de Gröbner permet deduir fàcilment moltes propietats importants de l'ideal i de la varietat algebraica associada, com la dimensió i el nombre de zeros quan és finita. El càlcul d'una base de Gröbner és una de les eines principals per a la resolució de sistemes d'equacions polinòmiques, així com pel càlcul d'imatges de varietats algebraiques per projeccions.

Es pot interpretar el càlcul de bases de Gröbner com una generalització multivariant i no lineal tant de l'algorisme d'Euclides per al màxim comú divisor de polinomis, com de l'eliminació gaussiana per a sistemes lineals.

A la seva tesi doctoral de 1965, Bruno Buchberger introduí la noció de base de Gröbner, juntament amb un algorisme per calcular-les (algorisme de Buchberger). Les bases de Gröbner reben aquest nom pel matemàtic austríac Wolfgang Gröbner, tutor de Buchberger. L'any 2007, Buchberger fou guardonat amb el Paris Kanellakis Theory and Practice Award de l'Association for Computing Machinery per la seva obra. Tanmateix, el matemàtic rus Nicolai Maksimovic Gjunter introduí una noció similar l'any 1913, publicada en diverses publicacions matemàtiques russes. Aquestes publicacions van ser ignorades per la comunitat matemàtica fins a la seva redescoberta l'any 1987 per Bodo Renschuch et al. El 1964, Heisuke Hironaka desenvolupà un concepte anàleg per a anells locals, amb el nom de bases estàndard.

Diversos autors han ampliat la teoria de les bases de Gröbner. Algunes generalitzacions inclouen la seva aplicació a polinomis sobre anells d'ideals principals o anells de polinomis, així com a algunes classes d'anells no commutatius i àlgebres, com àlgebres d'Ore.

Rerefons

Anell de polinomis

Article principal: Anell de polinomis

Les bases de Gröbner es defineixen principalment per a ideals d'un anell de polinomis $R=K[x_{1},\ldots ,x_{n}]$ sobre un cos K. Encara que la teoria és vàlida per a qualsevol cos, la majoria de càlculs de bases de Gröbner es fan quan K és o bé el cos dels racionals o bé els enters mòdul un nombre primer.

Un polinomi és una suma $c_{1}M_{1}+\cdots +c_{m}M_{m}$, on els coeficients $c_{i}$ són elements no nuls de K i els $M_{i}$ són monomis (productes de variables elevades a certa potència). És a dir, un monomi M és un producte $M=x_{1}^{a_{1}}\cdots x_{n}^{a_{n}}$, on els $a_{i}$ són nombres no negatius. El vector $A=[a_{1},\ldots ,a_{n}]$ s'anomena vector d'exponents de M. Aquesta notació s'acostuma a abreujar com $x_{1}^{a_{1}}\cdots x_{n}^{a_{n}}=X^{A}$. Cada monomi està unívocament determinat pel seu vector d'exponents, de tal manera que els ordinadors poden representar eficientment els monomis com a vectors d'exponents, i els polinomis com a llistes de vectors d'exponents i llurs coeficients.

Si $F=\{f_{1},\ldots ,f_{k}\}$ és un conjunt finit de polinomis sobre un anell de polinomis R, l'ideal generat per un conjunt F és el conjunt de combinacions lineals d'elements de F amb coeficients que recorren tot R:

$\langle f_{1},\ldots ,f_{k}\rangle =\left\{\sum _{i=1}^{k}g_{i}f_{i}\;|\;g_{1},\ldots ,g_{k}\in K[x_{1},\ldots ,x_{n}]\right\}.$

Ordre monomial

Totes les operacions relacionades amb les bases de Gröbner necessiten haver escollit prèviament un ordre total sobre els monomis, amb les següents propietats de compatibilitat amb la multiplicació: per a monomis qualssevol M, N, P,

1. $M\leq N\Longleftrightarrow MP\leq NP$
2. $M\leq MP$.

Sovint es diu que un ordre total que satisfaci aquestes condicions és un ordre admissible.

Aquestes condicions impliquen que l'anell és noetherià, la qual cosa vol dir que tota successió de monomis estrictament decreixent és finita.

Encara que la teoria de bases de Gröbner no depèn de l'elecció de l'ordenació admissible de monomis, hi ha tres ordenacions que són especialment importants:

• Ordre lexicogràfic, sovint anomenat lex o plex ((anglès) pure lexical ordering, ordre purament lexicogràfic)
• Ordre lexicogràfic invers de graus totals, sovint anomenat degrevlex ((anglès) Total degree reverse lexicographical ordering)
• Ordre d'eliminació, anomenat lexdeg

Inicialment, la teoria de bases de Gröbner s'introduí per a l'ordre lexicogràfic. Aviat s'observà que la base de Gröbner amb ordre degrevlex és més senzilla de calcular, i que és més fàcil calcular una base de Gröbner lex si primer es calcula la base degrevlex i després s'aplica un "algorisme de canvi d'ordenació". Quan es necessita aplicar l'eliminació, no és convenient aplicar degrevlex. Es poden emprar tant lex com lexdeg, però amb lexdeg molts càlculs són relativament senzills, i gairebé impossibles amb lex.

Un cop fixada una ordenació, els termes d'un polinomi (és a dir, cada producte d'un monomi amb el seu coeficient no nul) apareixen ordenats naturalment en ordre decreixent de monomis. Això permet representar un polinomi com una llista ordenada de parells (coeficient, vector d'exponents), que resulta ser una representació canònica del polinomi. El primer terme (és a dir, el més gran) d'un polinomi p i els corresponents monomi i coeficient s'anomenen respectivament terme principal, monomi principal i coeficient principal, i es denoten per lt(p), lm(p) i lc(p) ((anglès) respectivament, leading term, leading monomial i leading coefficient).

Reducció

El concepte de reducció, també anomenada divisió multivariant o càlcul de la forma normal, és cabdal en la teoria de bases de Gröbner. És una generalització multivariant de la divisió euclidiana de polinomis univariants.

En aquesta secció suposem que s'ha fixat una ordenació de monomis, que no està definida explícitament.

Donats dos polinomis f i g, es diu que f és reductible per g si algun monomi m de f és múltiple del monomi principal lm(g) de g. Si m és el monomi principal de f llavors es diu que f és principal-reductible per g. Si c és el coeficient de m a f i m = q lm(g), la reducció d'un pas de f per g és l'operació que associa a f el polinomi

$\operatorname {red} _{1}(f,g)=f-{\frac {c}{\operatorname {lc} (g)}}\,q\,g.$

Les principals propietats d'aquesta operació són que el polinomi resultant no conté el monomi m, i que els monomis més grans que m (segons l'ordre monomial escollit) queden intactes. En general, aquesta operació no està definida unívocament; si hi ha diversos monomis de f que són múltiples de lm(g), hom pot escollir de forma arbitrària el monomi que es vol reduir. A la pràctica, és millor escollir el monomi més gran segons l'ordre monomial, perquè si no, les reduccions posteriors podrien reintroduir el monomi que s'ha eliminat.

Donat un conjunt finit G de polinomis, es diu que f és reductible o principal-reductible per G si és reductible o principal-reductible, respectivament, per un element de G. En aquest cas, es defineix $\operatorname {red} _{1}(f,G)=\operatorname {red} _{1}(f,g)$. La reducció (completa) de f per G consisteix en aplicar iterativament aquest operador $\operatorname {red} _{1}$ fins a obtenir un polinomi $\operatorname {red} (f,G)$ que sigui irreductible per G. Hom diu que aquesta és una forma normal de f per G. En general, aquesta forma no està unívocament definida (no és una forma canònica); el fet que no sigui única és el punt de partida de la teoria de bases de Gröbner.

Per tal de calcular bases de Gröbner, excepte al pas final, no és necessari realitzar una reducció completa; és suficient amb una reducció de principals, la qual cosa estalvia força càlculs.

La definició de reducció mostra que, si h és una forma normal de f per G, llavors tenim

$f=h+\sum _{g\in G}q_{g}\,g,$

on $q_{g}$ són polinomis. En el cas de polinomis univariants, si G es redueix a un sol element g, llavors h és el residu de la divisió euclidiana de f per g, q_g n'és el quocient, i l'algorisme de divisió és exactament el procés de reducció de principals. Per aquest motiu, alguns autors empren el terme divisió multivariant en comptes de reducció.

Definició formal

Una base de Gröbner G d'un ideal I d'un anell de polinomis R sobre un cos és un conjunt generador de I caracteritzat per qualsevol de les propietats següents, donat un ordre monomial:

• l'ideal donat pels termes principals de I està generat pels termes principals de la base G
• el terme principal de qualsevol polinomi de I és divisible pel terme principal d'algun polinomi de la base G
• la divisió multivariant de qualsevol polinomi de l'anell de polinomis R per G dona un residu únic
• la divisió multivariant per G de qualsevol polinomi de l'ideal I dona residu 0.

Totes aquestes propietats són equivalents; diferents autors utilitzen diferents definicions, depenent de l'àrea de coneixement que escullin. Les últimes dues propietats permeten realitzar càlculs en l'anell quocient R/I amb les mateixes construccions que en aritmètica modular. Un resultat conegut d'àlgebra commutativa estableix que les bases de Gröbner sempre existeixen, i es poden obtenir de manera efectiva per a qualsevol ideal començant amb un subconjunt generador.

La divisió multivariant requereix un ordre monomial (la base depèn de l'ordre escollit), i ordres diferents donen lloc, en general, a bases de Gröbner radicalment diferents. Dues de les ordenacions més comunes són l'ordre lexicogràfic, i l'ordre lexicogràfic de grau invers (també anomenat ordre de grau total). L'ordre lexicogràfic elimina variables, però les bases de Gröbner resultants acostumen a ser molt costoses de calcular. L'ordre lexicogràfic de grau invers acostuma a produir bases de Gröbner amb menys càlculs. En aquest ordre, primer es comparen els monomis per grau total, i els "empats" es resolen prenent el monomi més petit respecte de l'ordre lexicogràfic amb les variables invertides.

En molts casos (polinomis en un nombre finit de variables a coeficients complexos o, més en general, a coeficients en un cos qualsevol, per exemple), existeixen bases de Gröbner per a qualsevol ordre monomial. L'algorisme de Buchberger és el mètode més conegut per calcular-les. Altres mètodes són els algorismes F4 i F5 de Faugère, basats en els mateixos conceptes que l'algorisme de Buchberger, i aproximacions involutives, basades en idees de l'àlgebra diferencial. També existeixen tres algorismes per convertir una base de Gröbner respecte d'un ordre monomial a una altra base de Gröbner respecte d'un altre ordre monomial: l'algorisme FGLM, l'algorisme Hilbert Driven i l'algorisme del camí de Gröbner. Aquests algorismes s'utilitzen per calcular bases de Gröbner lexicogràfiques (més complicades) a partir de bases de Gröbner de grau total (més senzilles).

Hom diu que una base de Gröbner és reduïda si el coeficient principal de cada element de la base és 1 i cap monomi de cap element de la base es troba a l'ideal generat pels termes principals dels altres termes de la base. En el cas pitjor, el càlcul d'una base de Gröbner pot requerir temps exponencial o fins i tot exponencial doble en el nombre de solucions del sistema polinòmic (per als ordres lexicogràfic de grau invers i lexicogràfic, respectivament). Tot i aquestes fites superiors per a la complexitat, moltes bases de Gröbner, tant estàndard com reduïdes, es poden calcular a la pràctica, i la majoria de sistemes algebraics computacionals contenen rutines per calcular-les.

El concepte i els algorismes de la teoria de bases de Gröbner s'han generalitzat pel cas de submòduls de mòduls lliures sobre un anell de polinomis. Si L és un mòdul lliure sobre un anell R, llavors hom pot considerar R⊕L com a anell si es defineix el producte de dos elements de L que sigui 0. Aquest anell es pot identificar amb $R[e_{1},\ldots ,e_{l}]/\left\langle \{e_{i}e_{j}|1\leq i\leq j\leq l\}\right\rangle ,$ on $e_{1},\ldots ,e_{l}$ és una base de L. Això permet identificar un submòdul de L generat per $g_{1},\ldots ,g_{k}$ amb l'ideal de $R[e_{1},\ldots ,e_{l}]$ generat per $g_{1},\ldots ,g_{k}$ i els productes $e_{i}e_{j}$, $1\leq i\leq j\leq l$. Si R és un anell de polinomis, això redueix la teoria i els algorismes de bases de Gröbner per a mòduls a la teoria i els algorismes per a ideals.

El concepte i els algorismes de bases de Gröbner també admeten generalitzacions a ideals sobre diversos anells, commutatius o no, com els anells de polinomis sobre un anell d'ideals principals o sobre àlgebres de Weyl.

Exemple i contraexemple

Els zeros de f(x, y) formen la paràbola vermella; els zeros de g(x, y) formen les tres rectes verticals blaves. Llur intersecció consisteix en tres punts.

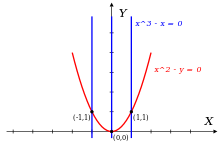
Sigui R = Q[x, y] l'anell de polinomis bivariants a coeficients racionals, i considerem l'ideal I = <f, g> generat pels polinomis:

f(x, y) = x² - y

g(x, y) = x³ - x

Els polinomis següents també són elements de I:

h(x, y) = -(x² + y - 1)f(x, y) + x·g(x, y) = y² - y

k(x, y) = -x·f(x, y) + g(x, y) = xy - x

Si s'estableix un ordre lexicogràfic on x > y, es té:

lt(f) = x²

lt(g) = x³

lt(h) = y²

L'ideal generat per {lt(f), lt(g)} només conté polinomis divisibles per x², la qual cosa exclou lt(h) = y²; per tant, {f, g} no és una base de Gröbner per a I.

Per altra banda, hom pot veure que {f, k, h} sí que és una base de Gröbner per a I.

Observem primer que f i g, i per tant h, k i qualsevol altre polinomi de l'ideal I, tenen aquests tres zeros en comú al pla (x, y), com es veu a la figura: {(1, 1), (-1, 1), (0, 0)}. Aquests tres punts no són colineals, d'on I no pot contenir cap polinomi de grau 1. Tampoc no pot contenir polinomis de la forma

m(x, y) = cx + p(y)

on c és un nombre racional no nul, i p un polinomi només en la variable y; un tal m no pot existir perquè no podria tenir dos zeros diferents pel mateix valor de y (en aquest cas, els punts (1, 1) i (-1, 1)).

Pel que hem vist, se segueix que I, a part del polinomi nul, només conté polinomis amb terme principal de grau igual o més gran a 2; per tant, els seus termes principals són divisibles per, almenys, un dels tres monomis {x², xy, y²} = {lt(f), lt(k), lt(h)}. Això significa que {f, k, h} és una base de Gröbner per a I respecte de l'ordre lexicogràfic amb x > y.

Propietats i aplicacions de les bases de Gröbner

Si no es diu el contrari, els resultats presentats en aquesta secció són certs per a qualsevol ordre monomial.

Hi ha la idea generalitzada, encara que incorrecta, de què és necessari emprar l'ordre lexicogràfic per a algun d'aquests resultats. De fet, l'ordre lexicogràfic acostuma a ser més costós de calcular, i, quan s'escull, es realitzen molts càlculs que són, en comparació, més senzills fer-los amb l'ordre lexicogràfic de grau invers (grevlex), o, de ser necessària l'eliminació, amb l'ordre d'eliminació (lexdeg), que restringeix grevlex en cada bloc de variables.

Igualtat d'ideals

Les bases de Gröbner reduïdes són úniques per a qualsevol ideal i qualsevol ordre monomial. Per tant, dos ideals són iguals si i només si tenen la mateixa base de Gröbner reduïda.

Pertinença i inclusió d'ideals

La reducció d'un polinomi f per la base de Gröbner G d'un ideal I dona 0 si i només si f pertany a I. Això permet comprovar la pertinença d'un element a un ideal. Un altre mètode consisteix a verificar que la base de Gröbner de G∪{f} és igual a G.

Per tal de verificar si l'ideal I generat per f₁, ...,f_k està contingut en l'ideal J, n'hi ha prou amb comprovar que tot f_i pertany a J. També es pot verificar la igualtat de les bases de Gröbner reduïdes de J i J∪{f₁, ...,f_k}.

Solucions d'un sistema d'equacions algebraiques

Qualsevol conjunt de polinomis es pot interpretar com un sistema d'equacions algebraiques, si s'igualen els polinomis a zero. El conjunt de solucions d'aquest sistema depèn només de l'ideal generat, i per tant no canvia quan se substitueix el conjunt generador per la base de Gröbner (independentment de l'ordenació) de l'ideal generat. Hom diu que una solució d'aquest sistema, amb coordenades en un cos algebraicament tancat que contingui els coeficients dels polinomis, és un zero de l'ideal. En el cas particular de coeficients racionals, hom acostuma a prendre el cos complex com a cos algebraicament tancat.

Un ideal no té cap zero (és a dir, el sistema d'equacions és inconsistent) si i només si el polinomi 1 pertany a l'ideal (aquest és el Nullstellensatz de Hilbert), o, equivalentment, si la seva base de Gröbner (per a qualsevol ordre monomial) conté l'1, o, també, si la corresponent base de Gröbner reduïda és {1}.

Donada la base de Gröbner G d'un ideal I, només té un nombre finit de zeros si i només si, per a tota variable x, G conté un polinomi amb un monomi principal que sigui potència de x (sense cap altra variable al terme principal). En aquest cas, el nombre de zeros, comptats amb la seva multiplicitat, és igual al nombre de monomis que no són múltiples de cap monomi principal de G. Es diu que aquest nombre és el grau de l'ideal.

Quan el nombre de zeros és finit, la base de Gröbner amb ordre monomial lexicogràfic proporciona, en teoria, una solució: les primeres coordenades d'una solució són una arrel del màxim comú divisor (m.c.d.) dels polinomis de la base que depèn només de la primera variable. Després de substituir aquesta arrel a la base, les segones coordenades d'aquesta solució són una arrel del m.c.d. de la resta de polinomis que depèn només de la segona variable, i així successivament. Aquest procés de resolució és només teòric, perquè implica computació de m.c.d. i resolució de polinomis a coeficients aproximats, la qual cosa no és pràctica, ja que es poden originar inestabilitat numèrica. Per tant, s'han desenvolupat altres mètodes de resolució de sistemes polinomials a través de bases de Gröbner.

Dimensió, grau i sèrie de Hilbert

La dimensió d'un ideal I en un anell de polinomis R és la dimensió de Krull de l'anell R/I, que al seu torn és igual a la dimensió del conjunt algebraic dels zeros de I. També és igual al nombre d'hiperplans en posició general que es necessiten per tenir una intersecció amb el conjunt algebraic, que és un nombre finit de punts. El grau de l'ideal i del seu conjunt algebraic associat és el nombre de punts d'aquesta intersecció finita, comptats amb multiplicitats. En particular, el grau d'una hipersuperfície és igual al grau del polinomi que la defineix.

Tant el grau com la dimensió depenen només del conjunt de monomis principals de la base de Gröbner de l'ideal, i no pas de l'ordre monomial que s'hagi escollit.

La dimensió és la grandària màxima d'un subconjunt S de les variables tal que no hi ha cap monomi principal que depengui només de les variables de S. Així, si l'ideal té dimensió 0, llavors per a tota variable x existeix un monomi principal a la base de Gröbner que és una potència de x.

Tant la dimensió com el grau es poden deduir a partir de la sèrie de Hilbert de l'ideal, que ve donada per la sèrie $\sum _{i=0}^{\infty }d_{i}t^{i}$, on $d_{i}$ és el nombre de monomis de grau i que no són múltiples de cap monomi principal de la base de Gröbner. La sèrie de Hilbert es pot sumar en forma de fracció racional

$\sum _{i=0}^{\infty }d_{i}t^{i}={\frac {P(t)}{(1-t)^{d}}},$

on d és la dimensió de l'ideal i $P(t)$ és un polinomi tal que $P(1)$ és el grau de l'ideal.

Encara que ni la dimensió ni el grau depenen de l'elecció de l'ordre monomial, tant la sèrie de Hilbert com el polinomi $P(t)$ poden canviar quan es canvia l'ordre monomial.

La majoria de sistemes algebraics computacionals que proporcionen funcions per al càlcul de bases de Gröbner també proporcionen funcions per calcular la sèrie de Hilbert, i per tant també permeten calcular-ne la dimensió i el grau.

Eliminació

El càlcul de bases de Gröbner per a un ordre monomial d'eliminació permet aplicar la teoria de l'eliminació computacional. Això està basat en el teorema següent.

Sigui un anell de polinomis $K[x_{1},\ldots ,x_{n},y_{1},\ldots ,y_{m}]=K[X,Y]$, on les variables estan dividides en dos subconjunts X i Y. Considerem també un ordre monomial d'eliminació que "elimini" X, és a dir, un ordre monomial per al qual es comparen dos polinomis en primer lloc mitjançant la comparació de les parts X i, només en cas d'igualtat, comparant després les parts Y. Això implica que un monomi que conté una variable de X és més gran que qualsevol monomi independent de X.

Si G és una base de Gröbner d'un ideal I per a aquest ordre monomial, llavors $G\cap K[Y]$ és una base de Gröbner de $I\cap K[Y]$ (hom acostuma a dir que aquest ideal és l'ideal d'eliminació). És més, un polinomi pertany a $G\cap K[Y]$ si i només si el seu terme principal pertany a $G\cap K[Y]$ (això fa més senzill el càlcul de $G\cap K[Y]$, ja que només cal comprovar els monomis principals).

Aquesta propietat d'eliminació té diverses aplicacions, algunes de les quals es veuen més endavant.

Una altra aplicació, en geometria algebraica, és que l'eliminació materialitza l'operació geomètrica de projecció d'un conjunt algebraic afí sobre un subespai de l'espai ambient: amb la notació anterior, la (clausura de Zariski de la) projecció del conjunt algebraic definit per l'ideal I sobre el subespai Y ve definida per l'ideal $I\cap K[Y]$.

L'ordre lexicogràfic tal que $x_{1}>\cdots >x_{n}$ és un ordre d'eliminació per a qualsevol partició $\{x_{1},\ldots ,x_{k}\},\{x_{k+1},\ldots ,x_{n}\}$. Així, una base de Gröbner per a aquest tipus d'ordre té molta més informació que la que es necessita habitualment. Aquest fet pot explicar que les bases de Gröbner per a un ordre lexicogràfic siguin més difícils de calcular.

Intersecció d'ideals

Si I i J són dos ideals generats respectivament per {f₁, ..., f_m} i {g₁, ..., g_k}, aleshores el càlcul d'una base de Gröbner conjunta proporciona una base de Gröbner per a la seva intersecció I ∩ J. Per tal de calcular-la de manera efectiva, hom introdueix una nova indeterminada t, i hom empra un ordre d'eliminació tal que el primer bloc només contingui t i l'altre bloc contingui la resta de variables (és a dir, un monomi que contingui t és més gran que qualsevol altre monomi que no contingui t). Amb aquest ordre monomial, una base de Gröbner de I ∩ J està constituïda pels polinomis independents de t, dins de la base de Gröbner de l'ideal

$K=\langle t^{2},tf_{1},\ldots ,tf_{m},(1-t)g_{1},\ldots ,(1-t)g_{k}\rangle .$

En altres paraules, I ∩ J s'obté per eliminació de t dins K. Això es pot demostrar mitjançant l'observació de què l'ideal K està format pels polinomis $(a-b)t+b$ tals que $a\in I$ i $b\in J$. Un tal polinomi és independent de t si i només si a=b, la qual cosa vol dir que $b\in I\cap J$.

Corbes racionals en forma implícita

Una corba racional és una corba algebraica que té una equació paramètrica de la forma

${\begin{aligned}x_{1}&={\frac {f_{1}(t)}{g_{1}(t)}}\\\vdots \\x_{n}&={\frac {f_{n}(t)}{g_{n}(t)}},\end{aligned}}$

on $f_{i}(t)$ i $g_{i}(t)$ són polinomis univariants per a 1 ≤ i ≤ n. Hom pot suposar, sense pèrdua de generalitat, que els polinomis $f_{i}(t)$ i $g_{i}(t)$ són coprimers (és a dir, que no tenen factors comuns llevat de constants).

Hom pot pensar en expressar aquestes corbes en forma implícita. En el cas de n = 2, és a dir, per a corbes planes, aquest càlcul es pot dur a terme mitjançant la resultant. L'equació implícita és, llavors, la següent resultant:

${\text{Res}}_{t}(g_{1}x_{1}-f_{1},g_{2}x_{2}-f_{2}).$

L'eliminació amb bases de Gröbner permet la transformació en forma implícita per a qualsevol valor de n; només cal eliminar t en l'ideal $\langle g_{1}x_{1}-f_{1},\ldots ,g_{n}x_{2}-f_{n}\rangle$. Si n = 2, el resultat és el mateix que amb la resultant, si l'aplicació $t\mapsto (x_{1},x_{2})$ és injectiva per a gairebé tot t. Altrament, la resultant és una potència del resultat de l'eliminació.

Saturació

Quan es modelitza un problema mitjançant equacions polinòmiques, és freqüent suposar que algunes quantitats siguin no nul·les perquè, si són iguals a zero, el problema esdevé molt diferent. Per exemple, quan tractem amb triangles, moltes propietats no són certes si el triangle és degenerat, és a dir, si la longitud d'un costat és igual a la suma de les longituds dels altres costats. En aquestes situacions, és força complicat deduir informació del sistema algebraic si no se'n descarten les solucions degenerades. Més precisament, el sistema d'equacions defineix un conjunt algebraic que pot tenir diverses components irreductibles, i hom ha d'eliminar les components on les condicions de degeneració són zero arreu.

Això s'aconsegueix per saturació de les equacions amb les condicions de degeneració, la qual cosa es pot realitzar emprant la propietat d'eliminació de les bases de Gröbner.

Definició de saturació

La localització d'un anell consisteix en afegir-li els inversos d'alguns elements. Aquesta secció tracta del cas d'un sol element, o equivalentment d'un nombre finit d'elements (afegir els inversos de diversos elements és equivalent a afegir l'invers del seu producte). La localització d'un anell R per un element f és l'anell $R_{f}=R[t]/(1-ft)$, on t és una nova indeterminada que representa l'invers de f. La localització d'un ideal I de R és l'ideal $R_{f}I$ de $R_{f}$. Quan R és un anell de polinomis, el càlcul de $R_{f}$ no és eficient, a causa de la necessitat de tractar els denominadors. Per tant, l'operació de localització se sol substituir per l'operació de saturació.

La saturació respecte de f d'un ideal I de R és la imatge inversa de $R_{f}I$ per l'aplicació canònica $R\to R_{f}$. És l'ideal $I:f^{\infty }=\{g\in R|(\exists k\in \mathbb {N} )f^{k}g\in I\}$ consistent en tots els elements de R tals que, multiplicats per alguna potència de f, pertanyen a I.

Si J és l'ideal generat per I i 1-ft a R[t], llavors $I:f^{\infty }=J\cap R$. Una conseqüència és que, si R és un anell de polinomis, el càlcul d'una base de Gröbner que elimini t permet calcular una base de Gröbner de la saturació d'un ideal per un polinomi.

La propietat més destacada de la saturació, que assegura que elimina, del conjunt algebraic definit per l'ideal $I$, les components irreductibles on el polinomi $f$ és zero, és la següent: La descomposició primària de $I:f^{\infty }$ consisteix en les components de la descomposició primària de $I$ que no contenen cap potència de $f$.

Càlcul de la saturació

Per tal d'obtenir una base de Gröbner de la saturació per f d'un ideal de polinomis generat per un conjunt finit de polinomis F, es pot eliminar t dins $F\cup \{1-tf\}$; és a dir, mantenint els polinomis independents de t dins la base de Gröbner de $F\cup \{1-tf\}$ per a un ordre d'eliminació que elimini t.

En comptes d'utilitzar F, hom pot començar amb una base de Gröbner de F. Depenent del problema que s'estigui tractant, un mètode pot ser més eficient que l'altre. Tot i això, si la saturació no elimina cap component, habitualment és més ràpid calcular primer la base de Gröbner de F. Per altra banda, si la saturació elimina alguna component, el càlcul directe pot ser sensiblement més ràpid.

Si es vol saturar respecte de diversos polinomis $f_{1},\ldots ,f_{k}$ o bé respecte d'un sol polinomi que sigui un producte $f=f_{1}\ldots f_{k}$, existeixen tres mètodes alternatius per tal d'aconseguir-ho, que proporcionen el mateix resultat, però poden tenir diferents esforços de càlcul (quin sigui el més eficient depèn de cada problema):

• Saturar per $f=f_{1}\ldots f_{k}$ en un sol càlcul de la base de Gröbner
• Saturar per $f_{1}$, després saturar el resultat per $f_{2}$, i així successivament
• Afegir a F o a la seva base de Gröbner els polinomis $1-t_{1}f_{1},\ldots ,1-t_{k}f_{k},$ i eliminar els $t_{i}$ en un sol càlcul de la base de Gröbner

Nullstellensatz efectiu

El Nullstellensatz de Hilbert té dues versions. La primera afirma que un conjunt de polinomis té un conjunt buut de zeros comuns en una clausura algebraica del cos de coeficients si i només si l'1 pertany a l'ideal generat. Això es pot comprovar fàcilment mitjançant el càlcul d'una base de Gröbner, perquè 1 pertany a un ideal si i només si 1 pertany a la base de Gröbner de l'ideal, per a qualsevol ordre monomial.

La segona versió afirma que el conjunt de zeros comuns (en una clausura algebraica del cos de coeficients) d'un ideal està contingut en la hipersuperfície dels zeros d'un polinomi f, si i només si una potència de f pertany a l'ideal. Això es pot comprovar mitjançant saturació de l'ideal per f; de fet, una potència de f pertany a l'ideal si i només si la saturació per f proporciona una base de Gröbner que només contingui 1.

Formalització implícita en dimensió superior

Per definició, una varietat racional afí de dimensió k es pot descriure mitjançant equacions paramètriques de la forma

${\begin{aligned}x_{1}&={\frac {p_{1}}{p_{0}}}\\\vdots \\x_{n}&={\frac {p_{n}}{p_{0}}},\end{aligned}}$

on $p_{0},\ldots ,p_{n}$ són n+1 polinomis en les k variables (els paràmetres de la parametrització) $t_{1},\ldots ,t_{k}$. Per tant, els paràmetres $t_{1},\ldots ,t_{k}$ i les coordenades $x_{1},\ldots ,x_{n}$ dels punts de la varietat són zeros de l'ideal

$I=\left\langle p_{0}x_{1}-p_{1},\ldots ,p_{0}x_{n}-p_{n}\right\rangle$.

Hom podria inferir que és suficient eliminar els paràmetres per tal d'obtenir les equacions implícites de la varietat, com s'ha vist en el cas de corbes. Malauradament, aquest no sempre és el cas. Si els $p_{i}$ tenen un zero comú (de vegades anomenat punt base), tota component irreductible del conjunt algebraic no buit definit pels $p_{i}$ és una component irreductible del conjunt algebraic definit per I. D'aquí es desprèn que, en aquest cas, l'eliminació directa dels $t_{i}$ proporciona un conjunt buit de polinomis.

Per tant, si k>1, hom necessita dos càlculs de bases de Gröbner per tal d'aconseguir la forma implícita de la varietat:

1. Saturar $I$ per $p_{0}$ per obtenir una base de Gröbner $G$
2. Eliminar els $t_{i}$ de $G$ per obtenir una base de Gröbner de l'ideal (de les equacions implícites) de la varietat

Implementacions

• CoCoA, sistema algebraic computacional lliure per al càlcul de bases de Gröbner
• GAP, sistema algebraic computacional lliure per al càlcul de bases de Gröbner
• FGb, implementació del mateix Faugère del seu algorisme F4, disponible com a llibreria de Maple A 2014 és, juntament amb Magma, la implementació més ràpida per a coeficients racionals i per a coeficients en un cos finit d'ordre primer.
• Macaulay 2, programari lliure per a realitzar càlculs amb polinomis, en particular per a l'obtenció de bases de Gröbner
• Magma té una implementació molt ràpida de l'algoriame F4 de Faugère.
• Maple té implementacions dels algorismes de Buchberger i F4 de Faugère, així com de la traça de Gröbner.
• Mathematica inclou una implementació de l'algorisme de Buchberger, juntament amb tècniques d'optimització com el camí de Gröbner, la traça de Gröbner, i una optimització pel cas de bases tòriques.
• SINGULAR, programari lliure per al càlcul de bases de Gröbner
• Sage proporciona una interfície unificada per diversos sistemes algebraics de computació, incloent SINGULAR i Macaulay, i inclou alguns algorismes propis per al càlcul de bases de Gröbner.
• SymPy, sistema algebraic computacional basat en Python que usa bases de Gröbner per a la resolució de sistemes algebraics

Bibliografia

• Adams, William W.; Loustaunau, Philippe. An Introduction to Gröbner Bases. 3. American Mathematical Society, 1994 (Graduate Studies in Mathematics). ISBN 0-8218-3804-0. 
• Aschenbrenner, Matthias; Hillar, Christopher J. «Finite generation of symmetric ideals». Trans. Amer. Math. Soc., 359, 2007, pàg. 5171–5192. (sobre bases de Gröbner de dimensió finita en anells de polinomis amb infinites indeterminades)
• Li, Huishi. Gröbner Bases in Ring Theory. World Scientific Publishing, 2011. ISBN 978-981-4365-13-0. 
• Becker, Thomas; Weispfenning, Volker. Gröbner Bases. 141. Springer Graduate Texts in Mathematics, 1998. ISBN 0-387-97971-9. 
• Buchberger, Bruno «An Algorithm for Finding the Basis Elements of the Residue Class Ring of a Zero Dimensional Polynomial Ideal, Ph.D. dissertation». Journal of Symbolic Computation. English translation by Michael Abramson, 41 (2006), 1965, pàg. 471–511. Aquesta és la tesi doctoral de Buchberger on creà les bases de Gröbner.
• Buchberger, Bruno «An Algorithmic Criterion for the Solvability of a System of Algebraic Equations». Aequationes Mathematicae, 4, 1970, pàg. 374–383. Traducció a l'anglès de Michael Abramson and Robert Lumbert a Gröbner Bases and Applications (B. Buchberger, F. Winkler, eds.). London Mathematical Society Lecture Note Series 251, Cambridge University Press, 1998, 535–545. ISBN 0-521-63298-6 (Aquesta és la publicació de la tesi de Buchberger.)
• Buchberger, Bruno; Kauers, Manuel «Gröbner Bases». Scholarpedia, 5, 2010, pàg. 7763. DOI: 10.4249/scholarpedia.7763.
• Fröberg, Ralf. An Introduction to Gröbner Bases. Wiley & Sons, 1997. ISBN 0-471-97442-0. 
• Sturmfels, Bernd «What is. .. a Gröbner Basis?». Notices of the American Mathematical Society, 52, 10, novembre 2005, pàg. 1199–1200.
• Širšov, Anatoly Illarionovich «Certain algorithmic problems for Lie algebras». ACM SIGSAM Bulletin, 33, 2, 1999, pàg. 3–6. DOI: 10.1145/334714.334715. (traduït de Sibirsk. Mat. Zh. Siberian Mathematics Journal, 3 (1962), 292–296)

Enllaços externs

• B. Buchberger, Groebner Bases: A Short Introduction for Systems Theorists in Proceedings of EUROCAST 2001.
• Buchberger, B. and Zapletal, A. Gröbner Bases Bibliography.
• Comparative Timings Page for Gröbner Bases Software
• Weisstein, Eric W., «Gröbner Basis» a MathWorld (en anglès).
• Introducció a les bases de Gröbner a Scholarpedia