Quàdrica: diferència entre les revisions
Cap resum de modificació |
|||
| Línia 1: | Línia 1: | ||
En [[matemàtiques]], una '''quàdrica''' o '''superfície quàdrica''' és una hipersuperfície definida en un [[espai vectorial]] n-dimensional, pels punts que anul·len un [[polinomi]] quadràtic. Si les [[coordenada|coordenades]] d'aquest espai són |
En [[matemàtiques]], una '''quàdrica''' o '''superfície quàdrica''' és una hipersuperfície definida en un [[espai vectorial]] n-dimensional, pels punts que anul·len un [[polinomi]] quadràtic. Si les [[coordenada|coordenades]] d'aquest espai són<math>\left\{x_{1},x_{2},...,x_{n}\right\}\,</math>, l'equació de qualsevol quàdrica en aquest espai serà: <math>\sum_{i,j=1}^{n}P_{i,j}x_{i}x_{j}+\sum_{k=1}^{n}Q_{k}x_{k}+R=0\,</math>, en què no tots els valors de<math>P_{(i,j)}\,</math> són iguals a <math>0\,</math>. |
||
En general, els coeficients d'aquesta equació seran valors de qualsevol [[Cos (matemàtiques)|cos]], sobre el |
En general, els coeficients d'aquesta equació seran valors de qualsevol [[Cos (matemàtiques)|cos]], sobre el qual s'ha definit l'[[espai vectorial]]. Malgrat això, a partir d'ara, només considerarem quàdriques sobre el cos <math>\mathbb{R}\,</math>. |
||
==Còniques== |
==Còniques== |
||
En el cas concret que <math>n=2\,</math>, les quàdriques resultants |
En el cas concret que <math>n=2\,</math>, les quàdriques resultants prenen el nom de [[cònica|''còniques'']], i l'anterior equació pren la forma: <math>(Ax^{2}+By^{2}+2Cxy)+(2Dx+2Ey)+F=0\,</math>. El nom de [[cònica|''còniques'']] prové del fet que es pot demostrar que qualsevol cònica és la intersecció d'un cert con per un determinat pla. L'equació anterior es pot escriure de la forma matricial següent: |
||
<math>X^\prime MX=0\,</math> |
<math>X^\prime MX=0\,</math> |
||
En què: |
|||
<math>X=\begin{pmatrix}x\\y\\1\end{pmatrix}\,</math> |
<math>X=\begin{pmatrix}x\\y\\1\end{pmatrix}\,</math> |
||
<math>M=\begin{pmatrix}A & C & D \\ C & B & E \\ D & E &F \end{pmatrix}\,</math> |
<math>M=\begin{pmatrix}A & C & D \\ C & B & E \\ D & E &F \end{pmatrix}\,</math> |
||
Segons la [[forma canònica]] que adopti la matriu |
Segons la [[forma canònica]] que adopti la matriu<math>M\,</math>, trobem les diferents solucions que tenen les còniques |
||
(<math>a,b,m\,</math> són valors reals, diferents de <math>0\,</math>): |
(<math>a,b,m\,</math> són valors reals, diferents de <math>0\,</math>): |
||
{| |
{| |
||
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=-1\,</math> |
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=-1\,</math> |
||
|[[el·lipse]] imaginària |
|[[el·lipse]] imaginària |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\,</math> |
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\,</math> |
||
|[[el·lipse]] real |
|[[el·lipse]] real |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=0\,</math> |
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=0\,</math> |
||
|dues [[recta|rectes]] imaginàries no paral·leles |
|dues [[recta|rectes]] imaginàries no paral·leles |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\,</math> |
|<math>\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\,</math> |
||
|[[hipèrbola]] |
|[[hipèrbola]] |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=0\,</math> |
|<math>\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=0\,</math> |
||
|dues [[recta|rectes]] reals no paral·leles |
|dues [[recta|rectes]] reals no paral·leles |
||
|- |
|- |
||
|<math>y=mx^{2}\,</math> |
|<math>y=mx^{2}\,</math> |
||
|[[paràbola]] |
|[[paràbola]] |
||
|- |
|- |
||
|<math>a^{2}x^{2}=-1\,</math> |
|<math>a^{2}x^{2}=-1\,</math> |
||
|dues [[recta|rectes]] imaginàries paral·leles |
|dues [[recta|rectes]] imaginàries paral·leles |
||
|- |
|- |
||
|<math>a^{2}x^{2}=1\,</math> |
|<math>a^{2}x^{2}=1\,</math> |
||
|dues [[recta|rectes]] reals paral·leles |
|dues [[recta|rectes]] reals paral·leles |
||
|- |
|- |
||
|<math>mx^{2}=0\,</math> |
|<math>mx^{2}=0\,</math> |
||
|dues [[recta|rectes]] coincidents |
|dues [[recta|rectes]] coincidents |
||
|- |
|- |
||
|<math>x=0\,</math> |
|<math>x=0\,</math> |
||
|una [[recta]] real |
|una [[recta]] real |
||
|} |
|} |
||
| Línia 52: | Línia 52: | ||
==Quàdriques== |
==Quàdriques== |
||
Més amunt hi ha la definició general de quàdrica. Però, normalment s'entén per quàdrica el cas concret en què <math>n=3\,</math>. En aquest cas, la matriu <math>M\,</math>, serà: de la forma: |
Més amunt, hi ha la definició general de quàdrica. Però, normalment, s'entén per quàdrica el cas concret en què <math>n=3\,</math>. En aquest cas, la matriu <math>M\,</math>, serà: de la forma: |
||
Si |
Si |
||
| Línia 60: | Línia 60: | ||
l'equació de la quàdrica serà també: <math>X^\prime MX=0\,</math> |
l'equació de la quàdrica serà també: <math>X^\prime MX=0\,</math> |
||
Si es |
Si es classifiquen les seves formes canòniques, es troba la llista següent: |
||
{| |
{| |
||
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=-1\,</math> |
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=-1\,</math> |
||
|[[el·lipsoide]] imaginari |
|[[el·lipsoide]] imaginari |
||
|[[Fitxer:Quadric Ellipsoid.jpg|150px|El·lipsoide]] |
|[[Fitxer:Quadric Ellipsoid.jpg|150px|El·lipsoide]] |
||
|- |
|- |
||
| Línia 74: | Línia 74: | ||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^2}{c^2}=1\,</math> |
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^2}{c^2}=1\,</math> |
||
|[[Hiperboloide| |
|[[Hiperboloide|hiperboloide d'un full]] |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}-\frac{z^2}{c^2}=1\,</math> |
|<math>\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}-\frac{z^2}{c^2}=1\,</math> |
||
|[[Hiperboloide| |
|[[Hiperboloide|hiperboloide de dos fulls]] |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^2}{c^2}=0\,</math> |
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^2}{c^2}=0\,</math> |
||
|[[ |
|[[con]] real |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+z=0\,</math> |
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+z=0\,</math> |
||
|[[Paraboloide| |
|[[Paraboloide|paraboloide el·líptic]] |
||
|[[Fitxer:Quadric Elliptic Paraboloid.jpg|150px|Paraboloide el·líptic]] |
|[[Fitxer:Quadric Elliptic Paraboloid.jpg|150px|Paraboloide el·líptic]] |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=-1\,</math> |
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=-1\,</math> |
||
| |
|superfície [[Cilindre|cilíndrica]] imaginària |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\,</math> |
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\,</math> |
||
| |
|superfície [[Cilindre|cilíndrica]] el·líptica |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=0\,</math> |
|<math>\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=0\,</math> |
||
| |
|dos [[pla|plans]] imaginaris no paral·lels |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}+z=0\,</math> |
|<math>\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}+z=0\,</math> |
||
|[[ |
|[[paraboloide]] hiperbòlic |
||
|[[Fitxer:Quadric Hyperbolic Paraboloid.jpg|150px| Paraboloide hiperbòlic]] |
|[[Fitxer:Quadric Hyperbolic Paraboloid.jpg|150px| Paraboloide hiperbòlic]] |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\,</math> |
|<math>\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\,</math> |
||
| |
|superfície [[Cilindre|cilíndrica]] hiperbòlica |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=0\,</math> |
|<math>\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=0\,</math> |
||
| |
|dos [[pla|plans]] reals no paral·lels |
||
|- |
|- |
||
|<math>x^{2}+mz=0\,</math> |
|<math>x^{2}+mz=0\,</math> |
||
| |
|superfície [[Cilindre|cilíndrica]] parabòlica |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}=-1\,</math> |
|<math>\frac{x^{2}}{a^{2}}=-1\,</math> |
||
| |
|dos [[pla|plans]] imaginaris paral·lels |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}=1\,</math> |
|<math>\frac{x^{2}}{a^{2}}=1\,</math> |
||
| |
|dos [[pla|plans]] reals paral·lels |
||
|- |
|- |
||
|<math>\frac{x^{2}}{a^{2}}=0\,</math> |
|<math>\frac{x^{2}}{a^{2}}=0\,</math> |
||
| |
|dos [[pla|plans]] reals coincidents |
||
|- |
|- |
||
|<math>x=0\,</math> |
|<math>x=0\,</math> |
||
| |
|un [[pla]] únic real |
||
|} |
|} |
||
També existeix la possibilitat d'un [[conjunt|conjunt buit]] i |
També existeix la possibilitat d'un [[conjunt|conjunt buit]] i la de tot l'[[espai]]. |
||
Revisió del 10:33, 19 jul 2015
En matemàtiques, una quàdrica o superfície quàdrica és una hipersuperfície definida en un espai vectorial n-dimensional, pels punts que anul·len un polinomi quadràtic. Si les coordenades d'aquest espai són, l'equació de qualsevol quàdrica en aquest espai serà: , en què no tots els valors de són iguals a . En general, els coeficients d'aquesta equació seran valors de qualsevol cos, sobre el qual s'ha definit l'espai vectorial. Malgrat això, a partir d'ara, només considerarem quàdriques sobre el cos .
Còniques
En el cas concret que , les quàdriques resultants prenen el nom de còniques, i l'anterior equació pren la forma: . El nom de còniques prové del fet que es pot demostrar que qualsevol cònica és la intersecció d'un cert con per un determinat pla. L'equació anterior es pot escriure de la forma matricial següent:
En què:
Segons la forma canònica que adopti la matriu, trobem les diferents solucions que tenen les còniques ( són valors reals, diferents de ):
| el·lipse imaginària | |
| el·lipse real | |
| dues rectes imaginàries no paral·leles | |
| hipèrbola | |
| dues rectes reals no paral·leles | |
| paràbola | |
| dues rectes imaginàries paral·leles | |
| dues rectes reals paral·leles | |
| dues rectes coincidents | |
| una recta real |
També existeix la possibilitat d'un conjunt buit i la de tot el pla.
Quàdriques
Més amunt, hi ha la definició general de quàdrica. Però, normalment, s'entén per quàdrica el cas concret en què . En aquest cas, la matriu , serà: de la forma: Si
l'equació de la quàdrica serà també:
Si es classifiquen les seves formes canòniques, es troba la llista següent:
| el·lipsoide imaginari | 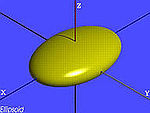
| |
| el·lipsoide real | ||
| con imaginari | ||
| hiperboloide d'un full | ||
| hiperboloide de dos fulls | ||
| con real | ||
| paraboloide el·líptic | 
| |
| superfície cilíndrica imaginària | ||
| superfície cilíndrica el·líptica | ||
| dos plans imaginaris no paral·lels | ||
| paraboloide hiperbòlic | 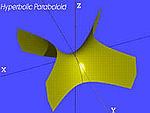
| |
| superfície cilíndrica hiperbòlica | ||
| dos plans reals no paral·lels | ||
| superfície cilíndrica parabòlica | ||
| dos plans imaginaris paral·lels | ||
| dos plans reals paral·lels | ||
| dos plans reals coincidents | ||
| un pla únic real |
També existeix la possibilitat d'un conjunt buit i la de tot l'espai.
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Quàdrica |





































