Girih

El girih (persa: گره, ‘nus’), també girih sāzī (گره سازی, ‘fer nusos') o girih chīnī (چینی), és un art decoratiu islàmic usat en arquitectura i en artesanies (cobertes de llibres, tapets, objectes petits de metall), consisteix en línies geomètriques les quals s'entrellacen formant un arranjament. En l'arquitectura iraniana, els patrons gereh sazi es veuen en treballs en maó banna'i, estuc i treballs en mosaic fayenza.[1] El girih ha estat definit com a "geomètric" (moltes vegades com a estel i polígon) els dissenys composts o generats d'arranjaments de punts, dels quals surten les de construcció i intersecten.[2]
En girih s'usen les formes simètriques amb vores rectes. El girih consisteix en un arranjament de línies que formen estels de 6, 8, 10 o 12 punts separades per polígons i línies, moltes vegades van ser dibuixades de manera entrellaçada. Tals patrons consisteixen usualment de repetir una "unitat" amb una simetria rotacional de 2, 3 o 6 vegades, això embona les unitats de manera que no existeix espai algun entre els elements repetits.[3]
L'equivalent tridimensional del girih és anomenat Mocàrab,[4] i és usat per decorar la part inferior de cúpules o voltes semicòniques.
Història
[modifica]

L'estil d'ornamentació es creu va ser inspirat pel treball de nusos de la província romana de Síria del segle II DC. El predecessor del girih eren treballs de línies i corbes amb una simetria rotacional triple. La Mesquita dels Omeies (709–715), a Damasc, Síria té pantalles en les finestres fetes de línies ondades entrellaçades en la forma d'estels de sis puntes.[5] Els barrots de les finestres al Khírbat al-Màfjar a Jericó (c. 730 AD) també tenen elements entrellaçats amb línies corbes.[6] També hi ha estuc esculpit amb formes de nusos en forma de corba a la Mesquita Jami a Nain, Iran (c. 960).[6] Alguns dels exemples arquitectònics de patrons geomètrics fets de línies es poden veure al portal del Mausoleu Arab Ata (S. X) al poblat de Tim, prop de Samarcanda, Uzbekistan i en Ribat-i Mahi, Iran (1019–1020).[7]
Il·luminació
[modifica]La forma més antiga de girih en un llibre es veu a la portada d'un manuscrit de l'Alcorà de l'any 1000, trobat en Bagdad.[8] Aquest alcorà té una pàgina il·luminada amb octàgons entrellaçats i cal·ligrafia thúluth.[9]
Treball en fusta
[modifica]
Un dels exemples més antics d'art geomètric en fusta data del segle xiii i és el minbar de la Mesquita d'Ibn Tulun al Caire.
Hi ha dos mètodes per crear patrons girih en la fusta. En el primer es fa una graella amb figures geomètriques (polígons i estels) després els forats poden ser omplerts amb algun altre material. D'altra banda en el segon mètode anomenat gereh-chini, es creen individualment panells amb figures geomètriques de fusta per després ser units i generar un disseny elaborat.[10] Aquesta tècnica per treballar la fusta va ser popular durant el període de l'Imperi Safàvida, alguns exemples es poden veure a diversos edificis històrics a Isfahan.
Arquitectura
[modifica]
El terme girih va ser usat en turc per denominar un patró poligonal de cintes (línies) que es va usar en arquitectura per primera vegada a finals del segle xv.[11] Per aquestes dates també els patrons van ser compilats per artesans en catàlegs de patrons com el Rotllo Topkapi.[12]
Encara que ja existien precedents curvilinis de girih des del segle x, els patrons girih no es van desenvolupar completament fins al segle xi a l'Iran. Es va tornar un element de disseny dominant durant els segles xi i xii, com per exemple els panells tallats d'estuc amb entrellaçats girih vists a les torres Kharraqan (1067) prop de Qazvín, Iran.[1][13] De vegades alguns arranjaments de plantes eren coordinats amb girih.[14]
Després del període Safàvida l'ús de girih va continuar durant els períodes de Seljuk i Il-kanat. Al segle xiv durant l'era Timúrida, girih es torna un element menor en les arts decoratives i és reemplaçat per patrons vegetals. No obstant això els treballs amb cintes geomètrics van continuar sent un element important en les arts decoratives en els monuments de l'Àsia central després del període de la dinastia timúrida.[1]
Construcció
[modifica]
|

| |
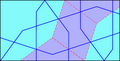
Un patró girih que es pot extreure amb regle i compàs.
|
Finestra de gàbia al Palau de Topkapı, construït amb el patró de l'esquerra.
|
Els primers patrons girih es van fer copiant plantilles de patrons sobre un reticle regular; els patrons eren dibuixats amb compàs i regle. Avui dia els artesans tradicionals usen tècniques com posar un parell de divisions per posar una marca d'incisió sobre una fulla de paper la qual ha estat deixada al sol per tornar-la fràgil. Es dibuixen línies rectes amb un llapis i un regle sense marques.[10] Els patrons girih fets d'aquesta forma semblen cristalls de dues dimensions tessel·lats, repetint en un plànol una unitat bàsica. Atès que la repetició de patrons es feia per translació o per rotació les unitats bàsiques tenien simetria rotacional doble, triple, quàdruple o sèxtuple.[15]
Rajoles girih
[modifica]Al voltant de l'any 1200, els patrons eren fets amb estels i polígons amb una simetria rotacional quíntuple (5) i dècuple (10). Tals figures també podien ser dibuixades amb compàs i regle. No obstant això als voltants del segle xv alguns patrons girih van deixar de ser periòdics. Tals patrons van ser construïts a partir de rajoles girih (repetició). Aquestes són un grup de cinc rajoles amb línies dibuixades sobre elles; quan s'uneixen sense deixar buits entre elles es forma el patró girih. Encara no se sap quan va ser la primera vegada que es van usar rajoles girih en comptes de construcció amb regle i compàs. Es considera que les rajoles girih es van utilitzar en alguns edificis al voltant del 1200.[16][17]
-
Rajoles girih.
-
Patró girih a partir de rajoles girih.
Disseny de doble nivell
[modifica]Els patrons girih al temple Darb-i Imam construït el 1453 a Isfahan tenien una complexitat molt més gran que en patrons anteriors. Els detalls en el patró suggereixen que es van utilitzar rajoles girih en comptes de regle i compàs. El patró al temple sembla aperiòdic gràcies al fet que en l'àrea de la paret on s'exhibeixen no formen un patró que es repeteixi de manera regular. Una altra característica dels patrons a Darb-i Imam és que estan dibuixats a dues escales diferents. Hi ha un patró que es veu quan s'observa a la distància, i un altre a menor escala que és part del primer i es veu a l'apropar-se a l'edifici.
Encara que hi ha evidència que algunes rajoles girih van usar una regla de subdivisió per dibuixar un patró de dos nivells, no hi ha cap exemple conegut d'una regla de subdivisió que es pugui repetir a nivells infinits. Per exemple, el patró utilitzat en el timpà del temple Darb-i Imam consisteix només de decàgons i monyos, mentre que la regla de subdivisió utilitza aquestes figures en conjunt amb el taulell (rajola) hexagonal allargat. Per tant aquest disseny no mostra auto-similaritat entre els nivells 1 i 2. No obstant això, un disseny de rajola que contingui decàgons i que tingui auto-similaritat resultat de l'aplicació repetitiva de la regla de subdivisió, resulta en un arranjament quasicristal·lí.[18]
Aperiodicitat
[modifica]Un enrajolat periòdic del pla és la repetició regular d'una "cèl·lula unitària" (la forma o grup de formes que és repetit) sense cap buit. Tals enrajolats poden ser vistos com a vidres bidimensionals, i donat el teorema de restricció cristal·logràfica, la cèl·lula unitària està restringida a una simetria rotacional doble, triple, quàdruple i sèxtuple. Per aquest motiu no és possible unir el pla periòdicament amb figures amb una rotació simètrica quíntuple tal com el d'una estrella de cinc puntes o un decàgon. Els patrons amb un ordre de translació perfecte quasi-periòdic poden tenir cristal·logràficament prohibicions de simetria rotacional com ara figures pentagonals o decagonals. Aquestes formes amb simetria quíntuple es repeteixen periòdicament, encara que en l'espai entre elles contenen altres figures que no tenen un patró periòdic; a aquest tipus d'enrajolat se l'anomena enrajolat quasicristal·lí.
Una manera de crear patrons quasi-periòdics és crear una tessel·lació de Penrose. Les rajoles girih poden ser subdividides en rajoles Penrose anomenades dart i kite però no hi ha evidència que aquest acostament fos usat pels artesans medievals.[16] Una altra manera de crear patrons quasi-periòdics és subdividint les rajoles (o cèl·lules unitàries) repetidament en rajoles girih més petites fent servir una regla de subdivisió. Al límit el pla se subdivideix en rajoles girih que es repeteixen amb freqüències aperiòdiques. L'ús d'aquesta regla de subdivisions hauria estat una evidència de que els artesans islàmics del segle xv sabien que les rajoles girih podien produir patrons que mai es repetissin exactament a si mateixos. No obstant això cap patró girih conegut fet amb rajoles girih mostra més de dos nivells de disseny. De fet no hi hauria una necessitat pràctica per tenir un patró girih que tingués més de dos nivells de disseny, perquè un tercer nivell seria d'una escala o massa petita o massa gran per ser percebuda. Sembla que els artesans islàmics medievals feien servir una eina que tenia la capacitat de crear patrons d'alta complexitat però mai es van adonar d'això, com diu E. Makovicky,[19]
| « | Els artesans estaven satisfets amb crear un gran domini fonamental sense preocupar-se amb les nocions matemàtiques de patrons quasi-periòdics extensibles indefinidament. No obstant això van entendre i van usar al seu favor algunes de les propietats geomètriques locals dels patrons quasicristal·lins que van construir. | » |
El rotllo Topkapi
[modifica]
El rotllo Topkapi data de finals del segle xviii, documenta els taulells (rajoles) girih que van ser usades per crear els patrons girih. Els dibuixos en aquest llibre de patrons mostren línies girih sobreposades amb els taulells usats per generar el patró.[16]
-
Panell del Rotllo Topkapi mostrant patrons girih a dues escales diferents i els taulells girih per construir-los.
-
Reconstrucció del patró de l'esquerra a escala petita (línies negres gruixudes), usant petits taulells girih.
-
Reconstrucció del patró de l'esquerra a gran escala (línies vermelles), usant grans taulells girih.
Galeria
[modifica]-
Pantalles de pedra girih a la tomba de Salim Chishti, Fatehpur Sikri, segle XVI
-
Girih en guix de l'Iwan de Hunat Hatun medersa, Kayseri
-
Girih en metall: estrella de 12 puntes a la porta de la mesquita de Sultan Hassan, el Caire
-
Girih en fusta: reixa a la Gran Mesquita de Còrdova
Referències
[modifica]- ↑ 1,0 1,1 1,2 Gereh Sazi. Encyclopaedia Iranica Online [Consulta: 1 de gener 2013]
- ↑ Terry Allen. Islamic Art and the Argument from Academic Geometry. 2004 [Consulta: 23 de gener 2012]
- ↑ Lee, A.J. Islamic Star Patterns. Muqarnas, volum 4, pàgines 182–197
- ↑ Notes on a recent study of the Topkapı scroll: a review article. Rogers, J.M. Bulletin of the School of Oriental and African Studies, University of London. Volum 60 número 3. Pàgines 433–439. Any 1997 doi:10.1017/s0041977x0003247x
- ↑ Umayyad Mosque, Damascus, Syria; Window screen, west vestibule. ArchNet[Enllaç no actiu] [Consulta: 12 de febrer 2012]
- ↑ 6,0 6,1 «Khirbat al-Mafjar shiero grill window». Khalili Research Centre.[Enllaç no actiu]
- ↑ Friday Mosque of Na'in, Na'in, Iran ArchNet[Enllaç no actiu] [Consulta: 2 de febrer 2012]
- ↑ Materials and Mediums. Pattern in Islamic Art Arxivat 2016-02-16 a Wayback Machine. [Consulta: 8 de febrer 2012]
- ↑ The transformation of Islamic art during the Sunni revival. I.B.Tauris. 2002. Pàgina 84 ISBN 978-1-85043-392-7
- ↑ 10,0 10,1 Pattern, Cognition and contemplation: una exploració the Geometric Art of Iran. Richard Henry. Iran Society 2007 PDF Arxivat 2014-06-11 a Wayback Machine. [Consulta: 8 de febrer 2012]
- ↑ Bir Belgeye Göre Amasya II. Bayezid Külliyesi. Dündar, A. Ankara Üniverstesi İlahiyat Fakültesi Dergisi. 2003 Volum 44, Num. 2, págines 131–172 PDF (turc)
- ↑ The Mathematics of Egypt, Mesopotàmia, Xina, Índia, and Islam. Katz, V.J. Princeton University Press. 2007. Pàgina 620. ISBN 978-0-691-11485-9
- ↑ Architecture – iv. Central Asian. Encyclopaedia Iranica 11 d'agost del 2011 [Consulta: 8 de febrer 2012]
- ↑ Urban development and architecture. G. A. Pugachenkova, A. H. Dani and Liu Yingsheng. History of Civilizations of Central Asia Volume IV: The Age of Achievement: A.D. 750 to the End of the Fifteenth Century – Part Two: The Achievements. ISBN 978-92-3-103654-5
- ↑ Cromwell, The Search for Quasi-Periodicity in Islamic 5-fold Ornament[Enllaç no actiu]. P.R. Mathematical Intelligencer. 2009. Volum 31, Num. 1, pàgines 36–56 2009 doi:10.1007/s00283-008-9018-6
- ↑ 16,0 16,1 16,2 Peter J. Lu and Paul J. Steinhardt. Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture. Science 2007. Volum 315, pàgines 1106–1110 PDF Arxivat 2009-10-07 a Wayback Machine. doi:10.1126/science.1135491. PMID: 17322056 Número 5815
- ↑ «Lu and Steinhardt, Supplementary figures». Arxivat de l'original el 2009-11-14. [Consulta: 1r juny 2017].
- ↑ Lu, Peter J.; Steinhardt, Paul J. «Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture» (en anglès). Science, 315, 5815, 2007, pàg. 1106–10. Bibcode: 2007Sci...315.1106L. DOI: 10.1126/science.1135491. PMID: 17322056.
- ↑ Emil Makovicky. Comment on "decagonal and Quasi-Crystalline Tilings in Medieval Islamic Architecture" [Consulta: 22 de febrer 2012]