Vidre d'espín
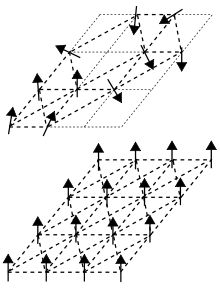
Un cristall d'espín és un imant desordenat amb interaccions frustrades que són augmentades per les posicions estocàstiques dels espins, on interaccions oposades, en concret enllaços ferromagnètics i antiferromagnètics, estan distribuïts aleatòriament amb una freqüència comparable. El terme «cristall» sorgeix de l'analogia entre el desordre magnètic a un cristall d'espín i l'ordre posicional d'un cristall químic convencional com el cristall de les finestres.
Els cristalls d'espín presenten moltes estructures metaestables resultant en un gran nombre d'escales temporals que són difícils d'explorar tan experimentalment com teòricament usant simulacions.
Component magnètic
[modifica]El tret distintiu entre els cristalls d'espín i altres sistemes magnètics és la dependència temporal. A una temperatura superior a la corresponent a la transició cap a un cristall d'espín, Tc,[note 1] el sistema exhibeix un comportament magnètic típic (com per exemple paramagnetisme).
Si s'aplica un camp magnètic tal com la mostra es refreda cap a la temperatura de transició, la magnetització de la mostra incrementa d'acord amb la llei de Curie. Quan s'arriba a Tc, la mostra es converteix en un cristall d'espín i si es continua refredant el sistema els canvis en la magnetització són molt petits. Aquesta propietat es coneix com a la magnetització de camp refredada. Quan el camp magnètic extern s'elimina, la magnetització del cristall d'espín decreix ràpidament fins a un valor més petit conegut com a magnetització romanent. Després la magnetització decreix més lentament acostant-se cap a zero (o cap a un nombre no zero però molt petit—aquest fet encara no es coneix). Aquesta reducció no és exponencial, i de fet cap funció simple serveix per descriure la corba de la magnetització segons el temps.[1] Aquesta reducció lenta és un tret distintiu dels cristalls d'espín. Mesures experimentals de durades de l'ordre dels dies mostren canvis continus per sobre del soroll extern degut a la instrumentació usada.[1]
Els cristalls d'espín difereixen dels materials ferromagnètics en el fet que quan el camp magnètic extern s'elimina, la magnetització roman indefinidament al valor romanent per als segons. Els materials paramagnètics es distingeixen dels cristalls d'espín perquè per a aquests materials la magnetització ràpidament decau fins a zero (sense magnetització romanent) quan el camp magnètic extern s'elimina. En tots els casos la reducció és ràpida i exponencial.
Si la mostra es refreda per sota de Tc en l'absència d'un camp magnètic extern, però un camp magnètic s'aplica després de la transició cap a la fase de cristall d'espín, aleshores hi ha un increment ràpid de la magnetització fins a un valor anomenat de camp zero refredat. Després d'això tenim un increment lent fins a la magnetització de camp refredada.
Sorprenentment, la suma de les dues funcions temporals complicades (les magnetitzacions de camp zero refredat i romanent) és una constant del valor de la magnetització de camp refredada, i per tant ambdues tenen la mateixa dependència temporal,[2] com a mínim per a camps externs suficientment petits.
El model d'Edwards–Anderson
[modifica]En aquest model tenim espins en una estructura -dimensional amb interaccions només amb els veïns més pròxims, de forma similar al model d'Ising. Aquest model es pot resoldre de forma exacta per a calcular les temperatures crítiques i una fase cristal·lina s'observa a baixes temperatures.[3] El Hamiltonià per a aquest sistema d'espins és:
on és la matriu de Pauli d'espín per a partícules d'espín un mig al punt de l'estructura. Un valor negatiu de descriu una interacció antiferromagnètica entre els espins als punts i . La suma inclou totes les posicions de veïns més pròxims per a una estructura en qualsevol dimensió. Les variables que descriuen la natura magnètica de la interacció espín-espín s'anomenen variables d'enllaç. Per calcular la funció de partició del sistema és necessari calcular la mitja de l'energia lliure on , per a tots els valors possible de . La distribució dels valors de es considera Gaussiana amb mitja i variança :
Resolent per trobar l'energia lliure usant el mètode de rèplica, a sota d'una certa temperatura, es troba la fase magnètica dels cristalls d'espín, que està caracteritzada per una magnetització zero i un valor no-zero de la funció de correlació de dos punts entre espins al mateix punt de l'estructura però per a dues rèpliques diferents: , on són els indexos de les rèpliques. Per tant, el paràmetre d'ordre per a la transició de fase entre el material ferromagnètic i el cristall d'espins és , i per a la transició material paramagnètic a cristall d'espins també és . Per tant el nou conjunt de paràmetres d'ordre que descriuen les tres fases magnètiques són ambdós i . L'energia lliure d'aquest sistema es pot trobar tant si s'assumeix la simetria entre rèpliques com si es considera un simetria trencada per a les rèpliques. Si s'assumeix la simetria entre rèpliques, l'energia lliure és
El model de Sherrington i Kirkpatrick
[modifica]A part de les propietats experimentals inusuals dels cristalls d'espín, aquests sistemes són l'objecte de moltes investigacions teòriques i computacionals. Una gran part del treball teòric inicial sobre cristalls d'espín considerava la teoria del camp mitjà basada en un conjunt de rèpliques de la funció de partició del sistema.
Un model central per als cristalls d'espín que es pot resoldre de forma exacta va ser introduït per D. Sherrington i S. Kirkpatrick l'any 1975. És un model d'Ising amb acoblaments frustrats de llarg abast tant ferro- com antiferromagnètics. Correspon a una teoria del camp mitjà dels cristalls d'espín que descriu la dinàmica lenta de la magnetització i l'estat d'equilibri no ergòdic.
A diferència del model d'Edwards–Anderson el rang de les interaccions pot ser infinit (de l'ordre de les dimensions del cristall), encara que només es considerin interaccions de parelles d'espins. Per tant, dos espins qualsevol es poden alinear amb un enllaç ferromagnètic o antiferromagnètic, i la distribució d'aquests ve donada exactament com al cas del model d'Edwards–Anderson. El Hamiltonià pel model de Sherrington i Kirkpatrick és molt semblant al del model d'Edwards–Anderson:
on tenen el mateix significat que al model d'Edwards–Anderson. La solució d'equilibri del model, després d'uns quants intents de Sherrington, Kirkpatrick i altres, va ser descoberta per Giorgio Parisi l'any 1979 usant el mètode de les rèpliques. La feina que va seguir aquesta solució per a interpretar-la—feta per M. Mezard, G. Parisi, M.A. Virasoro i molts altres—va revelar la naturalesa complexa d'una fase cristal·lina a baixes temperatures que es caracteritza pel trencament de l'ergodicitat i la ultrametricitat. Desenvolupaments posteriors varen portar a la creació del mètode de la cavitat que permet l'estudi de la fase de baixes temperatures sense usar el mètode de les rèpliques. Francesco Guerra i Michel Talagrand han proporcionat una demostració rigorosa de la solució de Parisi
El formalisme de la teoria del camp mitjà basada en un conjunt de rèpliques també s'ha aplicat a l'estudi de les xarxes neuronals, on ha permès calcular propietats com la capacitat de memòria d'una arquitectura senzilla de xarxa neuronal sense la necessitat d'algoritmes d'ensenyament (com el de propagació cap enrere).
També s'han estudiat extensament altres models de cristalls d'espín més realistes que inclouen interaccions frustrades de rang curt i desordre, com el model Gaussià on els acoblaments entre els espins segueixen una distribució Gaussiana. Aquest models s'han estudiat usant sobretot simulacions de Monte Carlo. Les fases del cristall d'espín a aquestes models estan delimitades per canvis d'estat ben delimitats.
Els cristalls d'espín han adquirit rellevància més enllà del camp de la matèria condensada, com per exemple a xarxes neuronals, informàtica, biologia teòrica, econofísica, etc.
Model de rang infinit
[modifica]El model de rang infinit és una generalització del model de Sherrington–Kirkpatrick, on no només es consideren interaccions entre parelles d'espins, sinó que interaccions entre espins, on i és el nombre total d'espins. A diferència del model d'Edwards–Anderson, però semblant al model de Sherrington–Kirkpatrick, el rang de les interaccions és infinit. El Hamiltonià d'aquest model és:
on tenen significats semblants que al model d'Edwards–Anderson. El límit d'aquest model es coneix com el model d'energia aleatòria. En aquest límit la probabilitat que el cristall d'espín existeixi en un estat particular només depèn de l'energia d'aquell estat i no en les configuracions concretes dels espins. Per resoldre el model se sol assumir una distribució Gaussiana per als enllaços magnètics. En principi, a conseqüència del teorema del límit central, qualsevol altra distribució hauria de donar el mateix resultat. La distribució Gaussiana, amb mitja i variança és:
Els paràmetres d'ordre d'aquest sistema són la magnetització i la funció de correlació de dos punts entre espins al mateix punt de l'estructura a dues rèpliques diferents, igual que al model de Sherrington–Kirkpatrick. Aquest model de rang infinit es pot resoldre per calcular l'energia lliure explícitament[3] en termes de i , si s'assumeix la simetria entre rèpliques o també si hi ha trencament de simetria per a una rèplica:[3]
Comportament no-ergòdic i aplicacions
[modifica]El comportament no ergòdic ocorre en cristalls d'espín per sota de la temperatura de congelació perquè per sota d'aquesta temperatura el sistema no pot escapar dels mínims ultra-profunds del relleu energètic desordenat jeràrquicament.[note 2] Malgrat que la temperatura de congelació normalment és al voltant dels 30 kelvin (-240 graus Celcius), i que podria semblar que el magnetisme dels cristalls d'espín no té aplicacions pràctiques a la vida de cada dia, existeixen aplicacions en diferents contextos. Per exemple, a la ja mencionada teoria de xarxes neuronals (és a dir, a la recerca teòrica del cervell), i la teoria matematico-econòmica de l'optimització.
Vegeu també
[modifica]Notes
[modifica]Referències
[modifica]- ↑ 1,0 1,1 J. Phys.: Condens. Matter, 10, 1998, pàg. 11049–11054..
- ↑ Nordblad, P.; Lundgren, L.; Sandlund, L. «A link between the relaxation of the zero field cooled and the thermoremanent magnetizations in spin glasses». Journal of Magnetism and Magnetic Materials, 54, 1986, p. 185–186. DOI: 10.1016/0304-8853(86)90543-3.
- ↑ 3,0 3,1 3,2 Nishimori, Hidetoshi. Statistical Physics of Spin Glasses and Information Processing: An Introduction. Oxford: Oxford University Press, 2001, p. 243. ISBN 0-19-850940-5, 9780198509400.
Bibliografia
[modifica]- Sherrington, David; Kirkpatrick, Scott «Solvable model of a spin-glass». Physics Review Letters, 35, 26, 1975, p. 1792–1796. DOI: 10.1103/PhysRevLett.35.1792.. Papercore Summary http://papercore.org/Sherrington1975 Arxivat 2013-04-15 at Archive.is
- Binder, K.; Young, A. P. «Spin glasses: Experimental facts, theoretical concepts, and open questions». Reviews of Modern Physics, 58, 1986, p. 801–976. DOI: 10.1103/RevModPhys.58.801..
- Bryngelson, Joseph D.; Wolynes, Peter G. «Spin glasses and the statistical mechanics of protein folding». Proceedings of the National Academy of Sciences, 84, 1987, p. 7524–7528. DOI: 10.1073/pnas.84.21.7524..
- Fischer, K. H.; Hertz, J. A.. Spin Glasses. Cambridge University Press, 1991..
- Mezard, Marc; Parisi, Giorgio; Virasoro, Miguel Angel. Spin glass theory and beyond. Singapore: World Scientific, 1987. ISBN 9971-5-0115-5.
- Mydosh, J. A.. Spin Glasses. Taylor & Francis, 1995..
- Parisi, G. «The order parameter for spin glasses: a function on the interval 0-1». J. Phys. A: Math. Gen., 13, 1980, p. 1101–1112. DOI: 10.1088/0305-4470/13/3/042. Papercore Summary http://papercore.org/Parisi1980 Arxivat 2013-04-15 at Archive.is.
- Talagrand, Michel «Replica symmetry breaking and exponential inequalities for the Sherrington–Kirkpatrick model». Annals of Probability, 28, 3, 2000, p. 1018–1062..
- Guerra, F.; Toninelli, F. L. «The thermodynamic limit in mean field spin glass models». Communications in Mathematical Physics, 230, 1, 2002, p. 71–79. DOI: 10.1007/s00220-002-0699-y..









![{\displaystyle f[J_{ij}]=-{\dfrac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/205976ab7fe6375400b4a296bd566c8993df6bd0)
![{\displaystyle {\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}e^{\left(-\beta H\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4bfedb44b0cca06446de8b0b0a0721cae51cb52)






















