Ondeta

Una ondetes és una funció matemàtica que divideix un senyal en diferents components freqüencials, i després estudien cada component amb una resolució que depèn de la seva escala.[1][2]
La transformada d'ondeta o transformada de Fourier[modifica]
La teoria de la transformada de Fourier diu que un senyal pot expressar-se com l'adició d'una sèrie, possiblement infinita de sinus i cosinus. Coneixem totes les components freqüencials del senyal, però no sabem on estan, és a dir, a quin temps està associat cada component freqüencial.[3] La solució aplicada aquí típicament és tallar el senyal en diferents parts i analitzar-les per separat. Però, en agafar instants de temps suficientment curts, la transformada de Fourier dona resultats no desitjats. Aquests efectes no desitjats són deguts al principi d'incertesa de Heisenberg, que, en termes de processament de senyals, indica que és impossible saber la freqüència exacta i el temps en què ocorre aquesta freqüència en un senyal.
La transformada d'ondeta resol aquest problema. La diferència bàsica respecte a Fourier és que les funcions bases (ondetes mare) tenen una duració finita, per tant ens permeten ubicar les components de freqüència en un instant de temps. En aquesta mena de transformada fem servir una finestra escalable que es desplaça pel senyal i calcula l'espectre per cada posició. Repetim aquest procés diverses vegades canviant la longitud de la finestra i s'obtenen una sèrie de representacions temps-freqüència del senyal; per això podem parlar d'una anàlisi multi-resolució. Per les ondetes no fem servir el terme representacions temps-freqüència, (freqüència es reserva per a transformades de Fourier) sinó de temps-escala. L'escala és inversament proporcional a la freqüència; així direm escala gran per parlar de tot el senyal i escala petita per fixar-nos ens els detalls. Per a les escales grans fem servir finestres grans, per a escales petites, finestres petites. Gràcies a aquest procés, la transformada d'oneta és més útil que no pas la de Fourier per a senyals que presenten pics o irregularitats no periòdiques.
Ondeta mare[modifica]
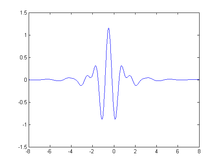
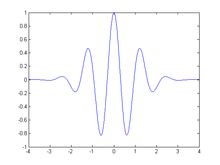
Totes les ondetes són variacions d'escala i translació d'una ondeta mare :[4]
Tota ondeta mare ha de complir la condició d'admissió
- ,
essent la transformada de Fourier de . Aquesta condició d'admissibilitat implica que la transformada de Fourier de s'anul·la per , és a dir,
- .
Això vol dir que tota ondeta ha de tenir un espectre pas-banda. D'altra banda, un zero a freqüència zero implica també que el valor mitjà de l'ondeta en el domini del temps ha de ser zero,
- i per tant, ha de ser oscil·latòria.
 |
 |
 |
Breu història[modifica]
- El 1807 Jean Baptiste Joseph Fourier (1768-1830) va desenvolupar l'anàlisi freqüencial que va rebre el seu nom. Això va obrir portes a càlculs totalment nous.[5] Després d'això, molts matemàtics van començar a investigar sobre anàlisi escalable. La primera referència que es té d'ondeta data del 1909 i apareix a l'apèndix de la tesi d'Alfred Haar.[6]
- En els anys 1830 nombrosos grups d'estudi independents van aprofundir sobre funcions base d'escala variable. Paul Lévy va veure que la funció base de Haar era superior a les funcions base de Fourier a l'hora d'analitzar detalls complicats al Moviment brownià.[7]
- Entre el 1960 i el 1980 els matemàtics Guido Weiss i Ronald R. Coifman van estudiar els elements més simples d'un espai de funcions, denominats àtoms, i van trobar la manera de reconstruir funcions fent servir aquests "àtoms". El 1980 Grossman i Morlet van definir el concepte d'ondeta en el context de la física quàntica.
- Després del 1980: El 1985 Stéphane Mallat va fer un gran treball d'investigació en processament digital d'imatge. Va descobrir relacions entre filtres mirall en quadratura, algorismes de piràmide i bases ortonormals d'ondícules.[8] Inspirat per aquest últim, Yves Meyer va idear les primeres ondícules no-trivials. Uns quants anys més tard, Ingrid Daubechies va fer servir el treball de Mallat per fer un conjunt de funcions base ortonormals que són la pedra angular de les ondetes d'avui en dia.[9]
Aplicacions de l'ondeta[modifica]
Igual que amb la Transformada de Fourier, hi ha la transformada contínua d'ondeta i transformada discreta d'ondeta. La contínua es fa servir en anàlisi de senyals i, per tant, en el camp de la investigació científica, mentre que la discreta té usos més pràctics com ara:[4]
- Compressió de dades.
- Eliminació de soroll.
- En comunicacions, per modular senyals.
- Detecció d'imatges.
Això ens dona usos tan variats com ara: la dinàmica molecular, l'astrofísica, l'òptica, l'estudi de les turbulències i la mecànica quàntica, el Processament digital d'imatges, les anàlisis de sang, l'anàlisi d'electrocardiogrames, l'estudi del ADN, l'anàlisi de proteïnes, la meteorologia, el processament de senyals en general, el Reconeixement de la parla, els gràfics per ordinador, l'anàlisi multifractal i en el camp de Bioestadística.
En el camp de la compressió de dades, hi ha el JPEG 2000, un estàndard de compressió d'imatges que es basa en la transformada discreta d'ondeta.
Referències[modifica]
- ↑ «transformada en ondeta contínua». Gran Enciclopèdia Catalana. Grup Enciclopèdia. [Consulta: 27 desembre 2018].
- ↑ Fra Paleo, Urbano. Diccionari terminològic de fotogrametria. Barcelona: Institut Cartogràfic de Catalunya, 2011. ISBN 978-84-393-8754-1.
- ↑ «A Really Friendly Guide To Wavelets [Un guia realment amable per comprendre ondetes]» (en anglès). Polyvalens, 2011. [Consulta: 14 febrer 2023].
- ↑ 4,0 4,1 Charles, Cathérine. «L’analyse par ondelettes dans la vie de tous les jours» (en francès). Interstices, 19-10-2021. [Consulta: 14 febrer 2023].
- ↑ Fourrie la va présentar el 1807, però fa trigar fins 1822 per trobar un editor.Fourier, Jean-Baptiste-Joseph. Théorie analytique de la chaleur, par M. Fourier (en francès). París: Firmin Didot, 1822, p. 1822.
- ↑ Haar, Alfred «Zur Theorie der orthogonalen Funktionensysteme, (Erste Mitteilung» (en alemany). Mathematische Annalen, 69, 1910, pàg. 331–371. ISSN: 0025-5831.
- ↑ Baleanu, Dumitru (ed.). Advances in Wavelet Theory and Their Applications in Engineering, Physics and Technology (en anglès). Rijeka: InTech. ISBN 953-51-0494-2.
- ↑ Nowal, Mathieu; Meyer, Yves «La surprenante ascension des ondelettes» (en francès). Mensuel 383, febrer 2005.
- ↑ Roberts, Siobhan «The Godmother of the Digital Image» (en anglès). The New York Times Magazine, 14-09-2021.
Bibliografia[modifica]
- Graps, Amara «An introduction to wavelets». IEEE Computational Science and Engineering, 2, 2, febrer 1995, pàg. 50–61. DOI: 10.1109/99.388960.
Enllaços externs[modifica]
- «Wavelets: ver el bosque y los árboles» (en castellà). U.S. National Academy of Sciences. Arxivat de l'original el 16 de setembre 2018. [Consulta: 14 febrer 2023].
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Ondeta |







