Tangent

Sigui C una corba, i A un punt d'aquesta se suposa que A és un punt regular de la corba, és a dir, que no és un punt angulós: la corba no canvia sobtadament de direcció en A.

La tangent a C en A és la recta TA que passa per A i que té la mateixa direcció que C al voltant d'A.

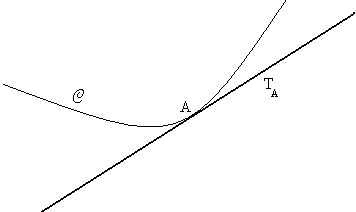
La tangent és la posició límit de la recta (AM) (anomenada corda de la corba), quan M és un punt de C que s'aproxima indefinidament al punt A (M es mou successivament per M1, M2, M3, M4 ...)

Si C representa una funció f (no és el cas en la gràfica precedent),llavors la recta (AM) tindrà com a coeficient director (o pendent):

$\frac {f(x) - f(a)} {x - a}$ (on a és l'abscissa d'A i x la de M).

Per tant, la pendent de la tangent TA serà:

$\lim_{x \to a} \frac {f(x) - f(a)} {x - a}$

És, per definició, f'(a), el nombre derivat d'f en a.

L'equació de la tangent és Ta:

y = f '(a)·(x - a) + f(a)

La recta ortogonal a la tangent TA que passa pel punt (a,f(a)) s'anomena recta normal i la seva pendent, en un sistema de coordenades ortonormals, ve donada per:

$\frac {-1} {f'(a)}$

La seva equació és:

y = - (x - a)/f '(a) + f(a)

Suposant, és clar, que f'(a) ≠ 0. Aquesta recta no intervé en l'estudi general de les funcions però si en problemes geomètrics relacionats amb les còniques, com per exemple, per poder determinar el punt focal d'una paràbola.

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Tangent