Autòmat cel·lular

Un autòmat cel·lular (A.C.) és un model matemàtic per a un sistema dinàmic que evoluciona en passos discrets. És adequat per modelar sistemes naturals que puguin ser descrits com una col·lecció massiva d'objectes simples que interaccionin localment uns amb els altres.[1][2]
Són sistemes descoberts dins de l'àmbit del camp de la física computacional per John von Neumann els anys 1950.[3] Tot i això, els autòmats cel·lulars van ser posats ja en pràctica per Konrad Zuse i Stanislaw Ulam uns anys abans.[4]
Descripció[modifica]
No hi ha una definició formal i matemàtica acceptada d'autòmat cel·lular però es pot descriure com una tupla, és a dir, un conjunt ordenat d'objectes caracteritzat pels següents components:
- Una reixeta o quadriculat de nombres enters (conjunt ) infinitament estesa, i amb dimensió . Cada cel·la de la quadrícula rep el nom de cèl·lula.
- Cada cèl·lula pot prendre un valor en a partir d'un conjunt finit d'estats .
- Cada cèl·lula, a més, es caracteritza pel seu veïnatge, un conjunt finit de cèl·lules als seus voltants.
- D'acord amb això, s'aplica a totes les cèl·lules de la quadrícula una funció de transició () que pren com arguments els valors de la cèl·lula en qüestió i els valors de les cel·les veïnes, i torna el nou valor que la cèl·lula tindrà en la següent etapa de temps. Aquesta funció s'aplica de forma homogènia a totes les cèl·lules per cada pas discret de temps.
Condicions de frontera[modifica]
Per definició, un autòmat cel·lular consisteix en una retícula infinita d'enters. Tot i això, per qüestions pràctiques (com en models de sistemes físics duts a terme en ordinadors de memòria finita), es requereix prendre certes consideracions a l'hora d'implementar un autòmat. Per aquest motiu, la definició original es modifica per donar cabuda a retícules finites en les que les cèl·lules de l'autòmat interactuïn. Això comporta la consideració extra del que ha de succeir en aquelles cèl·lules que es trobin als marges de la retícula, el que es coneix com a condició de frontera.
Es poden implementar diverses condicions de frontera, en funció d'allò que el problema real requereixi pel seu modelat. Per exemple:
- Frontera oberta. Fora de la graella hi resideixen cèl·lules, totes amb un valor fix. En el cas particular del joc de la vida i altres autòmats similars amb dos estats al seu conjunt , una frontera s'anomena "freda" si les cèl·lules fora de la graella es consideren mortes, i "calenta" si es consideren vives.
- Frontera periòdica. Es considera que la graella té una propietat toroidal, com si els seus extrems es toquessin. Per tant, si una cèl·lula surt de la graella, reapareix pel costat oposat.
- Frontera reflectora. Les cèl·lules de fora la graella reflecteixen els valors de les de les de dins. Així, una cèl·lula que toqués la frontera per fora agafaria com a valor el de la cèl·lula que toca la frontera per dins.
- Sense frontera. Fent ús d'implementacions que facin créixer dinàmicament l'ús de memòria de la graella implementada, es pot assumir que cada vegada que les cèl·lules han d'interactuar amb les de fora de la graella, aquesta es fa més gran per dur a terme aquestes interaccions. Tot i tendir a infinit, atès que la frontera inicial és finita no és equivalent a la definició general de l'autòmat cel·lular, perquè en aquest cas no pots activar qualsevol cèl·lula de la graella des del principi.
Variacions[modifica]
Alguns autòmats cel·lulars tenen graella triangular o hexagonal enlloc de rectangular. També existeixen versions tridimensionals o amb moltes més dimensions, com en el cas dels autòmats cel·lulars quàntics. Altres possibles variacions són augmentar el nombre d'estats que cada cèl·lula pot tenir (com en el cas dels autòmats cel·lulars totalistes), la funció de transició de manera que ja no sigui homogènia, utilitzar elements estocàstics (aleatorietat) en (el que es coneix com a autòmat cel·lular probabilístic) o variar els veïnatges de cada cèl·lula.
Aplicacions[modifica]

Els autòmats cel·lulars es poden usar per a modelar nombrosos sistemes físics que es caracteritzin per un gran nombre de components homogenis i que interaccionin localment entre ells. De fet, qualsevol sistema real al que se li puguin analogar els conceptes de "veïnatge", "estats dels components" i "funció de translació" és candidat per ser modelat per un A.C.
Les característiques dels autòmats cel·lulars faran que siguin discrets en temps, espai o les dues coses, depenent de la variant de la definició de A.C. que s'utilitzi. Alguns exemples d'ús són:
- Modelat de flux de trànsit de vehicles i de vianants.
- Modelat de fluxs (gasos o líquids).
- Modelat de l'evolució de cèl·lules o virus com el VIH.
- Modelat de processos de percolació.
Exemples d'autòmats cel·lulars[modifica]
Autòmat cel·lular unidimensional[modifica]
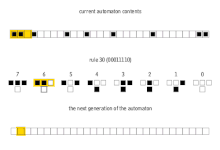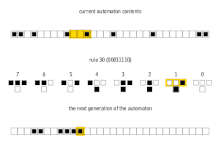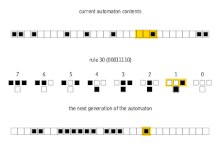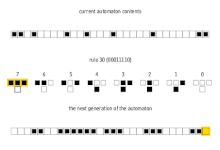

L'exemple més bàsic d'autòmat cel·lular no trivial és la versió unidimensional. Es defineix una seqüència de cèl·lules que només poden tenir dos estats, i es llegeixen ordenadament aplicant canvis segons l'estat de la cèl·lula i les seves veïnes (cèl·lula anterior i posterior). El resultat es sol mostrar com una nova línia a sota de l'actual que serà la llegida a continuació, i aquest procés es va repetint. El conjunt de normes que defineix el valor de la nova cèl·lula segons els estats de les cèl·lules comprovades s'anomena Rule Set, i hi ha 256 casos diferents.[5]
Per comprovar l'efecte al llarg del temps d'un determinat Rule Set, s'aplica a una seqüència senar de cèl·lules on totes estan desactivades excepte la del mig. A partir d'aquesta configuració inicial, els Rule Sets es poden classificar en amfiquirals o no amfiquirals segons si el patró format és simètric. A més, els patrons obtinguts es poden classificar en:[1]
- Uniformes. Es genera un patró pla, on totes les cel·les acaben tenint el mateix estat. Exemple: Rule 222.
- Oscil·lants. Es tendeix a un patró regular, per exemple [A, A, B, A, A, B ...] en el cas de Rule 190.
- Atzarosos. S'obté un patró de pseudo-aleatorietat. Exemple: Rule 30.
- Complexes. S'obtenen patrons regulars complexes, per exemple el Rule 110. Un altre exemple intessant és el Rule 90, on s'obté un patró similar al Triangle de Sierpinski.
Autòmat de Von Neumann[modifica]
L'autòmat de Von Neumann és considerat el primer autòmat cel·lular, ideat per John von Neumann a partir dels suggeriments de Stanislaw Ulam. El seu propòsit original era proporcionar informació sobre els requisits lògics per a fer una màquina autoreplicant, i es van utilitzar en el constructor universal de Von Neumann.[3]
Les cèl·lules, és a dir els autòmats finits, estan disposades sobre un pla cartesià i interfereixen amb les quatre cèl·lules veïnes, formant diferents estats de transmissió de senyals, el resultat del qual pot ser la construcció o destrucció de circuits. Cada cèl·lula pot tenir 29 estats diferents, ordenats en cinc grups: buit, transitori, confluent, transmissor ordinari i transmissor especial. Així doncs, els estats "excitats" transporten dades, a la velocitat d'un bit per pas de transició d'estat i aplicant canvis sobre la graella.
Existeixen diverses variants similars; l'autòmat de Nobili incorpora la capacitat de les cèl·lules confluents de creuar senyals i emmagatzemar informació, i l'autòmat de Hutton permet replicar un bucle de dades anàleg als bucles de Langton.[6]
L'autòmat de Codd va ser proposat per Edgar F. Codd al 1968 per recrear la universalitat de càlcul i construcció de l'autòmat de von Neumann però amb només 8 estats.[7] De manera similar, Edwin Roger Banks en va fer un de només 4 estats, anomenat autòmat Banks IV però que finalment no va implementar.[8] Al 1973, John Devore va optimitzar l'autòmat de Codd per reduir-ne la mida de la màquina autoreplicant. Christopher Langton va fer una modificació de l'autòmat de Codd per crear els bucles de Langton, els quals són autoreplicants amb moltes menys cel·les però ja no tenen universalitat de càlcul i construcció.[9]
Bucles de Langton[modifica]

Els bucles de Langton són "espècies" amb vida artificial que consisteixen en un bucle de cèl·lules que contenen informació genètica, que flueix contínuament al voltant del bucle i surten al llarg d'un "braç" (pseudòpode) que es convertirà en el bucle fill. Els "gens" li indiquen que faci tres girs a l'esquerra, completant el bucle, que després es desconnecta del seu pare. Els bucles són incapaços de reproduir-se a l'espai que ocupa un altre bucle, per això un cop estan envoltats pels bucles fills es consideren "morts". Igual que amb l'autòmat de Codd, els bucles de Langton consisteixen en senyals que viatgen passivament al llarg dels circuits, fins que arriben als extrems oberts, on s'executa l'ordre que porten.
Els bucles de Langton formen tota una familia d'autòmats cel·lulars amb característiques similars:
- Bucles de Langton originals (1984) creats per Christopher Langton.[9]
- Bucles de Byl (1989), amb una reducció de la mida del bucle al treure'n l'espai interior.[10]
- Bucles de Chou-Reggia (1993), amb reducció total de les parets del bucle.[11]
- Bucles de Tempesti (1995), amb noves capacitats de construcció, permetent escriure patrons dins del bucle després de la reproducció.[12]
- Bucles de Perrier (1996), fent-lo universalment computable.[13]
- Bucle SDSR (1998), amb un estat addicional que permet la dissolució d'estructures; cada bucle té una vida útil limitada i es dissol al final del seu cicle de vida. Això permet un creixement continu al llarg de les generacions.[14]
- Evoloop (1999), extensió del bucle SDSR que és capaç d'interaccionar amb bucles veïns, així com d'evolucionar a causa de la competència per l'espai, on la selecció natural afavoreix els bucles funcionals més petits.[15][16]
- Sexyloop (2007), modificació de l'Evoloop on els bucles auto-reproduïbles tenen la capacitat de reproducció sexual. Amb aquesta capacitat, els bucles són capaços de transferir material genètic a altres bucles. Això augmenta la diversitat en l'evolució de noves espècies de bucles.[17]
Joc de la vida[modifica]
El joc de la vida és un autòmat ortogonal bidimensional bàsic, creat per John Horton Conway el 1970. A cada unitat de temps, es donen les següents transicions:[18]
- Tota cel·la viva amb menys de dos veïns vius mor (de solitud).
- Tota cel·la viva amb més de tres veïns vius mor (de sobreconcentració).
- Tota cel·la viva amb dos o tres veïns vius, segueix viva per a la següent generació.
- Tota cel·la morta amb exactament tres veïns vius torna a la vida.
Per fer la comprovació s'utilitza el veïnatge de Moore, és a dir, les 8 cel·les veïnes de cada cel·la; adjacents i diagonals. Aquesta idea comprèn tot un seguit d'autòmats amb característiques similars, i per tant de la mateixa família que el joc de la vida.[19] En són exemples les llavors de Brian o el cervell de Brian, creades per Brian Silverman.[20]
En les llavors totes les cel·les vives moren i les mortes viuen si tenien exactament n veïns vius. El cervell de Brian és més complex; es parteix del joc de la vida però les cel·les tenen tres estats; vives, morint-se o mortes.[21]
Wireworld[modifica]
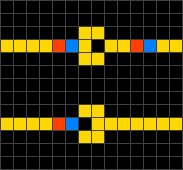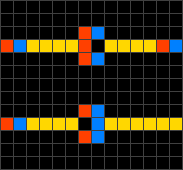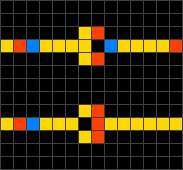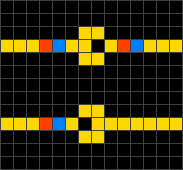
Wireworld és una modificació del joc de la vida on la majoria de cel·les no es poden activar, i la resta formen circuits conductors on les cel·les actives representen els electrons. Va ser proposat per Brian Silverman per simular transistors i portes lògiques. A més, Wireworld és Turing complet.[22]
Es defineixen quatre tipus de cel·les: buida, cap d'electró, cua d'electró i conducte.
- Tota cel·la buida segueix sent buida.
- El cap d'electró passa a ser cua.
- La cua d'electró passa a ser conducte.
- El conducte forma un cap d'electró si una o dues cel·les veïnes són caps d'electró, si no segueix sent conducte.
Formiga de Langton[modifica]
La formiga de Langton és un autòmat ortogonal bidimensional creat per Chris Langton. En aquest cas es defineix una cel·la especial que actua de formiga que es va desplaçant, i al fer-ho modifica els estats de les altres cel·les (al trepitjar una cel·la activada la desactiva, i al revés). La direcció de la formiga depèn de l'estat de la cel·la actual a la que es troba, si està activada fa un gir a dreta, si està desactivada fa un gir a l'esquerra.
Tot això és recreable com un autòmat normal definint més estats possibles per cada cèl·lula, segons si s'hi troba la formiga, segons la direcció d'aquesta i segons si la casella a la que es troba està activada o desactivada.[23]
Model Nagel-Schreckenberg[modifica]
El model Nagel-Schreckenberg és un autòmat cel·lular probabilístic unidimensional creat per Kai Nagel i Michael Schreckenberg que serveix de model simple de trànsit vehicular. En aquest cas el que varia segons els vehicles veïns és la velocitat del vehicle, i a més hi ha una certa probabilitat que el vehicle freni sense un motiu aparent.[24]
Autòmat d'Ulam–Warburton[modifica]
L'autòmat d'Ulam–Warburton (UWCA) és un autòmat ortogonal bidimensional que té la particularitat de que les cel·les activades no es poden tornar a desactivar. A cada iteració s'activen les cel·les inactivades en què només un dels costats és adjacent ortogonalment a una d'activada.[25]
CoDi[modifica]
CoDi (Collect and Distribute) va ser ideat per Felix Gers l'any 1998 per crear xarxes neuronals d'impulsos, és a dir xarxes neuronals artificials que mimetitzen les xarxes neuronals naturals. Utilitza una versió tridimensional del veïnatge de Neumann, on cada cèl·lula veu sis cèl·lules veïnes.[26]
En fase de creixement, es crea una xarxa neuronal a l'espai de l'autòmat, basada en un cromosoma subjacent que ha estat distribuït al llarg de l'espai de l'autòmat de manera que cada cèl·lula en té una còpia. Hi ha quatre tipus de cèl·lules: cossos de les neurones (base estructural), axons, dendrites i espai no ocupat. Un cop finalitzada la fase de creixement s'inicia la fase de senyalització (o processament); els senyals són distribuïts des dels cossos neuronals a través del seu axó i recollits de les dendrites de connexió. CoDi no utilitza sinapsi de manera explícita, perquè les dendrites que estan en contacte amb un axó en recullen els senyals neuronals directament.[26]
Referències[modifica]
- ↑ 1,0 1,1 Wolfram, Stephen «Universality and Complexity in Cellular Automata». Physica D, 10, 1984, pàg. 1-35.
- ↑ Hedlund, G. A. «Endomorphisms and Automorphisms of the Shift Dynamical System». Mathematical Systems Theory, 3, 4, 1969.
- ↑ 3,0 3,1 von Neumann, John. Arthur W. Burks. Theory of self-reproducing automata. Urbana, University of Illinois Press, 1966.
- ↑ Zuse, Konrad «Rechnender Raum, Schriften zur Datenverarbeitung Band». Friedrich Vieweg & Sohn, Braunschweig, 1969.
- ↑ Kari, J. «The Nilpotency Problem of One-dimensional Cellular Automata». SIAM Journal on Computing, 21, 1992, pàg. 571-586.
- ↑ Buckley, William R. «(PDF) Signal crossing solutions in von Neumann self-replicating cellular automata.», 01-01-2008.
- ↑ Codd, Edgar F.. Cellular Automata. Academic Press, New York, 1968.
- ↑ Banks, Edwin. Information Processing and Transmission in Cellular Automata. PhD thesis, MIT, Department of Mechanical Engineering, 1971.
- ↑ 9,0 9,1 Langton, C. G. «Self-Reproduction in Cellular Automata». Physica D: Nonlinear Phenomena, 10, 1-2, 1984, pàg. 135–144. DOI: 10.1016/0167-2789(84)90256-2.
- ↑ J. Byl «Self-Reproduction in small cellular automata». Physica D, 34, 1–2, 1989, pàg. 295–299. DOI: 10.1016/0167-2789(89)90242-X.
- ↑ «Simple systems that exhibit self-directed replication». Science, 259, 5099, 1993, pàg. 1282–1287. DOI: 10.1126/science.259.5099.1282. PMID: 17732248.
- ↑ G. Tempesti (1995). "A New Self-Reproducing Cellular Automaton Capable of Construction and Computation". Advances in Artificial Life, Proc. 3rd European Conference on Artificial Life: 555–563, Granada, Spain: Lecture Notes in Artificial Intelligence, 929, Springer Verlag, Berlin
- ↑ «Toward a viable, self-reproducing universal computer». Physica D, 97, 4, 1996, pàg. 335–352. DOI: 10.1016/0167-2789(96)00091-7.
- ↑ Sayama, Hiroki (1998). "Introduction of Structural Dissolution into Langton's Self-Reproducing Loop". Artificial Life VI: Proceedings of the Sixth International Conference on Artificial Life: 114–122, Los Angeles, California: MIT Press
- ↑ Sayama, Hiroki (1999). "Toward the Realization of an Evolving Ecosystem on Cellular Automata". Proceedings of the Fourth International Symposium on Artificial Life and Robotics (AROB 4th '99): 254–257
- ↑ «Complex genetic evolution of artificial self-replicators in cellular automata». Complexity, 10, 2, 2004, pàg. 33–39. Arxivat de l'original el 2013-01-05. DOI: 10.1002/cplx.20060 [Consulta: 8 desembre 2020]. Arxivat 2013-01-05 at Archive.is
- ↑ (2007) "Sexyloop: Self-Reproduction, Evolution and Sex in Cellular Automata". The First IEEE Symposium on Artificial Life (April 1–5, 2007, Hawaii, USA): 130–138
- ↑ Gardner, Martin «The fantastic combinations of John Conway's new solitaire game 'life'». Scientific American, 223, 1970, pàg. 120-123.
- ↑ Wójtowicz, Mirek «Cellular Automaton Rules Lexicon - Family: Life». Mirek's Cellebration. Arxivat de l'original el 2021-01-25 [Consulta: 15 octubre 2020]. Arxivat 2021-01-25 a Wayback Machine.
- ↑ Silverman, Brian. «Changing the Rules». The Virtual Computer. Mathematical Association of America. Arxivat de l'original el 2 de juliol de 2013.
- ↑ Resnick, Mitchel. «Exploring Emergence: The Brian Rules». MIT Media Laboratory, Lifelong Kindergarten Group, 04-02-1996. Arxivat de l'original el 2008-12-23.
- ↑ Dewdney, A. K. «Computer recreations: The cellular automata programs that create Wireworld, Rugworld and other diversions». Scientific American, 262, 1, 1990, pàg. 146-149. JSTOR: 24996654.
- ↑ Gajardo, A.; Moreira, A.; Goles, E. «Complexity of Langton's ant». Discrete Applied Mathematics, 117, 1-3, 2002, pàg. 41-50. DOI: 10.1016/S0166-218X(00)00334-6.
- ↑ Nagel, K.; Schreckenberg, M. «A cellular automaton model for freeway traffic». Journal de Physique I, 2, 12, 1992, pàg. 2221. Arxivat de l'original el 2014-03-11. Bibcode: 1992JPhy1...2.2221N. DOI: 10.1051/jp1:1992277. Arxivat 2014-03-11 a Wayback Machine.
- ↑ Applegate, David; Pol, Omar E.; Sloane, N. J. A. (2010). «The toothpick sequence and other sequences from cellular automata». Proceedings of the Forty-First Southeastern International Conference on Combinatorics, Graph Theory and Computing. Congressus Numerantium. 206. pp. 157–191. arXiv: 1004.3036. Bibcode: 2010arXiv1004.3036A. MR: 2762248.
- ↑ 26,0 26,1 Gers, Felix; Hugo Garis; Michael Korkin. «CoDi-1Bit : A simplified cellular automata based neuron model». A: Artificial Evolution. 1363, 1998, p. 315–333. DOI 10.1007/BFb0026610. ISBN 978-3-540-64169-8.
Vegeu també[modifica]
Bibliografia[modifica]
- S. Wolfram, A New Kind of Science, 2002 (anglès) [Consulta: 28 març 2020]
- B. Cipra, What's happening in the Mathematical Sciences, vols. 3 y 5, American Mathematical Society, EU, 1996, 2002
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Autòmat cel·lular |
- Una Introducción a los Autómatas Celulares, arxivat de l'original (castellà)
- Autómata Celular (castellà)
- MathWorld - Elementary Cellular Automaton - Llista de tots els Rule Sets en la versió unidireccional (anglès)




