Gas
| Mecànica dels medis continus |
|---|
 |
|
|
Un gas és un estat de la matèria en què les forces interatòmiques o intermoleculars entre els diferents àtoms o molècules d'una substància són tan petites que la substància no adopta ni forma ni volum fix, tendint a expandir-se tant com sigui possible per ocupar el recipient que el conté.
A nivell microscòpic un gas es caracteritza pel fet que les seues partícules estan molt separades i la interacció entre elles és molt baixa.
Una substància gasosa pot liquar-se per refredament o per compressió, fins a una certa temperatura anomenada temperatura crítica. Per sobre de la temperatura crítica, si comprimim un gas obtindrem un fluid supercrític i no un líquid.
El nom "gas" ve de la pronunciació neerlandesa del mot grec "caos", que s'usava des del segle xvi per referir-se a l'aire, el químic flamenc Jan Baptista van Helmont va proposar la seva utilització aplicada al gasos al segle xvii.
Propietats físiques
[modifica]

La majoria dels gasos són difícils d'observar amb els nostres ulls, només els podem descriure a partir de propietats físiques o característiques a nivell macroscòpic: la seva pressió, el volum, el nombre de partícules (agrupades en mols pels químics) i la temperatura. Aquestes quatre característiques van ser repetidament observades per científics com Robert Boyle, Jacques Charles, John Dalton, Joseph-Louis Gay-Lussac i Amedeo Avogadro per a molts gasos i en diferents condicions. Els seus detallats estudis van portar a trobar una relació matemàtica entre aquestes quatre propietats que s'expressa per mitjà de la llei dels gasos ideals (vegeu més avall).
Les partícules que formen el gas es troben àmpliament separades les unes de les altres, i per tant la influència d'una partícula sobre les adjacents no serà la mateixa que la que trobem en el cas dels sòlids o els líquids. Degut a la naturalesa electromagnètica de les partícules hi ha un camp de força al seu voltant, les interaccions entre aquests camps de força són conegudes amb el terme de forces intermoleculars. En tant que càrregues, les que tenen el mateix signe es repel·leixen i les que són de diferent signe s'atreuen. Els gasos formats per ions porten una càrrega elèctrica permanent i formen molècules polars amb enllaços covalents. Aquests enllaços produeixen una concentració permanent de la càrrega a les molècules, mentre que als compostos la càrrega neta és nul·la, les càrregues transitòries existeixen als enllaços covalents de les molècules i són conegudes com les forces de van der Waals. Aquestes forces intermoleculars influencien el moviment de les partícules en funció de la distància, i en conseqüència afecten les seves propietats termodinàmiques. A la temperatura i pressió característiques de moltes aplicacions, les partícules són habitualment molt separades i aquesta separació es correspon a una força atractiva molt petita, de manera que la força intermolecular esdevé negligible per a moltes d'aquestes aplicacions. La interacció de les forces intermoleculars varia en funció del gas i influeix en les seves propietats físiques característiques.[1][2]
Un gas també presenta les següents característiques:
- Baixa densitat i viscositat relatives comparades amb els estats sòlid i líquid.
- Es poden expandir i contraure molt amb els canvis de temperatura o de pressió, d'aquí que se'ls apliqui el terme “compressibles.
- Es poden difondre fàcilment, separant-se per tal d'ocupar de manera homogènia qualsevol contenidor.
- La solubilitat d'un gas en un líquid, a l'inrevés que la d'un sòlid, disminueix amb la temperatura.
Comportament a escala macroscòpica
[modifica]Quan s'analitza un sistema gasós, és habitual especificar un marc de referència o escala de longitud. Una escala de longitud gran pot correspondre a una visió macroscòpica del sistema, mentre que una escala de longitud més petita correspon a una visió microscòpica. El sistema ha de ser prou gran (en volum) com per contenir un nombre prou gran de partícules, de manera que l'anàlisi estadística resultant ens ofereixi uns resultats que concordin amb el comportament mitjà del sistema, parlem de la velocitat, la temperatura o la pressió de les partícules del sistema.
A escala macroscòpica, les quantitats que es mesuren són en termes dels efectes a gran escala que té el gas sobre un sistema o el seu medi, com per exemple la velocitat, la pressió o la temperatura. Hi ha moltes eines matemàtiques per analitzar les propietats d'un gas, però quan les condicions són més extremes les eines esdevenen molt més complexes. Equacions matemàtiques, com per exemple les equacions hidrodinàmiques esteses, les equacions de Navier-Stoker i les equacions d'Euler, han estat desenvolupades per intentar modelar les relacions de la pressió, la densitat, la temperatura i la velocitat d'un gas en moviment.[3] Boyle va poder arribar a les seves conclusions només amb l'ajuda de l'àlgebra perquè va estudiar els gasos a pressions relativament baixes, dintre dels límits on el seu comportament és ideal. Però avui dia l'alta tecnologia ens ofereix eines que ens permeten explorar el comportament de sistemes de gasos que no es comporten de manera ideal. Eines com l'estadística o el càlcul multivariable fan possible la solució a les complexes situacions dinàmiques com podrien ser les de la reentrada a l'atmosfera d'un vehicle espacial, on el comportament dels gasos no segueix el model ideal i on cal assegurar-se que les condicions no afectaran les propietats del material de la nau.
Pressió
[modifica]La pressió que exerceix un gas uniformement a través de la superfície d'un contenidor es pot descriure mitjançant teoria cinètica simple. Les partícules d'un gas es mouen contínuament en direccions aleatòries i sovint col·lideixen amb les parets del contenidor i/o entre elles. Totes aquestes partícules presenten les magnituds físiques de massa, moment i energia, que han de ser conservades. En la mecànica clàssica, el moment és, per definició, el producte de la massa i la velocitat. L'energia cinètica és la meitat de la massa multiplicada per la velocitat al quadrat. La suma de tots els components normals de la forca exercida per les partícules que impacten a les parets del contenidor dividida per l'àrea de les parets és definida com la pressió. Aleshores, es pot dir que la pressió és el moment lineal mitjà d'aquestes partícules en moviment. Un error comú és creure que les col·lisions de les molècules entre elles són essencials per explicar la pressió d'un gas, però en realitat la seva velocitat aleatòria és suficient per definir aquesta quantitat.
Temperatura
[modifica]La velocitat de les partícules d'un gas és proporcional a la seva temperatura termodinàmica. La temperatura de qualsevol sistema físic és el resultat del moviment de les seves partícules, les molècules i els àtoms que el componen. En la mecànica estadística, la temperatura és la mesura de l'energia cinètica mitjana emmagatzemada a una partícula. Els mètodes d'emmagatzemament d'aquesta energia són dictats pels graus de llibertat de la partícula en si (modes d'energia). L'energia cinètica afegida a les partícules d'un gas a conseqüència de processos endotèrmics també produeix moviment lineal, rotacional o vibratori, en canvi, en els sòlids només pot tenir com a conseqüència l'augment de la vibració de les molècules atès que l'estructura cristal·lina evita els moviments lineals o rotatoris. A un gas escalfat les partícules tenen una variació de la velocitat més gran i aquesta canvia contínuament degut a les col·lisions amb altres partícules. La variació en velocitat se sol descriure amb la distribució de Maxwell-Boltzmann. La utilització d'aquesta distribució implica gasos ideals a prop de l'equilibri termodinàmic per al sistema de partícules considerat.
Volum específic
[modifica]Quan es duu a terme una anàlisi termodinàmica, és habitual parlar de les propietats intensives i extensives. Les propietats que depenen de la quantitat de gas són les propietats "extensives", mentre que les que no en depenen són les propietats "intensives". El volum específic és un exemple d'una propietat intensiva, car és el volum ocupat per una unitat de massa d'un material, cosa que vol dir que el volum ha estat dividit per la massa per tal d'obtenir una quantitat en termes de, per exemple,. Cal destacar que la diferència entre volum i volum específic és que la quantitat específica és independent de la massa.
Densitat
[modifica]Com que les molècules tenen un moviment lliure dins d'un gas, la massa del gas se sol determinar mitjançant la seva densitat. La densitat és la massa d'una substància dividida pel volum o, més simplement, l'invers del volum específic. Pels gasos, aquesta densitat pot variar significativament perquè les molècules tenen moviment lliure. Macroscòpicament, la densitat és una variable d'estat d'un gas i el canvi de densitat durant qualsevol procés és regit per les lleis de la termodinàmica. Com que hi ha moltes partícules en un moviment completament aleatori, per un gas estàtic, la densitat és igual a tot el contenidor. Per tant, la densitat és una magnitud escalar; és una quantitat física simple que té una magnitud però que no té cap direcció associada. Es pot mostrar per la teoria cinètica que la densitat és proporcional a la mida del contenir en què es troba una massa fixa de gas.
Comportament a escala microscòpica
[modifica]Si fos possible observar un gas a través d'un microscopi prou potent com per veure les partícules que el formen (molècules, àtoms, ions), les veuríem movent-se d'una manera més o menys aleatòria. Aquestes partícules que formen el gas només canvien la direcció del seu moviment quan col·lideixen amb una altra partícula o contra les parets del contenidor. Si considerem que aquestes col·lisions són perfectament elàstiques, podrem considerar la substància com un gas ideal. El comportament de les partícules a nivell microscòpic és descrit per la teoria cinètica molecular dels gasos.
Teoria cinètica molecular
[modifica]La teoria cinètica molecular explica el comportament i les propietats macroscòpiques dels gasos a partir d'una descripció de la seva composició i del moviment de les partícules a nivell microscòpic. Aquesta teoria es basa en una sèrie de postulats, com per exemple: 1) La matèria està constituïda per partícules,; 2) Les partícules exerceixen entre si forces d'atracció que les mantenen unides; 3) Les partícules són en moviment constant. En funció dels postulats que considerem la teoria serà més o menys complexa, en la seva expressió més simple permet arribar a la llei d'Avogadro o llei dels gasos perfectes.
La teoria explica com responen els sistemes gasosos als canvis, per exemple, si escalfem un gas, la seva energia interna (la seva temperatura) s'incrementarà. A mesura que s'escalfa el gas observarem que les seves partícules també aniran incrementant la seva velocitat. Si observem la pressió, constatarem que amb el gas escalfat ha augmentat el nombre de col·lisions amb les parets del contenidor a causa de l'increment de la velocitat de les partícules a causa de l'augment de la temperatura, a mesura que el nombre de col·lisions contra les parets del contenidor augmenten per unitat de temps la pressió s'incrementa de manera proporcional.
Moviment brownià
[modifica]El moviment brownià és un model matemàtic que s'utilitza per descriure el moviment aleatori de les partícules immerses a un fluid. L'animació de la dreta il·lustra com aquest comportament provoca la dispersió dels gasos (entropia). Aquest comportament també és descrit per la física de partícules. Atès que l'observació individual de les partícules d'un gas (àtoms o molècules) al límit (o més enllà) de la tecnologia actual, només els càlculs teòrics aporten suggeriments sobre com es mouen, però el seu moviment és diferent de moviment brownià.
Forces intermoleculars
[modifica]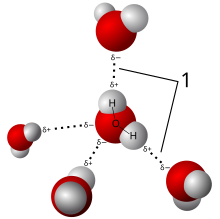
Les atraccions o repulsions momentànies entre les partícules tenen un efecte sobre la dinàmica del gas. En química física, el nom que reben les forces intermoleculars és el de forces de van der Waals. Aquestes forces tenen un paper en la determinació de les propietats físiques d'un gas, com per exemple la seva viscositat o el seu flux volumètric. Si ignorem aquestes forces en determinades condicions podrem tractar un gas real com si fos un gas ideal, aquesta assumpció ens permetrà utilitzar la llei dels gasos ideals. La correcta utilització d'aquestes relacions als gasos requereix tornar a la teoria cinètica molecular. Quan les partícules del gas posseeixen una càrrega magnètica o força intermolecular la seva influència sobre les altres molècules s'incrementa a mesura que es redueix l'espai que hi ha entre elles. En absència de càrregues, a un punt determinat on l'espai entre els partícules s'ha reduït prou ja no es poden evitar les col·lisions entre les partícules a una temperatura normal. Una altra via per incrementar el nombre de col·lisions entre les partícules d'una gas seria escalfar un determinat volum fix de gas, a més temperatura més velocitat de les partícules i més probabilitat que hi hagi col·lisions. Tot això significa que aquestes equacions ideals ens proporcionen un resultats raonables excepte per a casos amb una gran pressió o temperatura (ionització). Aquestes condicions excepcionals permeten la transferència d'energia a l'interior del gas, i és precisament l'absència de transferències internes d'energia el que ens permet parlar de condicions ideals, a les que l'intercanvi d'energia només es produeix als límits del sistema. Els gasos reals experimenten algunes d'aquestes col·lisions i forces intermoleculars, però mentre siguin estadísticament negligibles els resultats de les equacions ideals continuaran essent vàlids. D'altra banda, quan les partícules d'un gas són comprimides de manera que són molt properes les unes de les altres, el gas es comporta de manera més semblant a un líquid.
Models dels gasos
[modifica]L'equació d'estat d'un gas és un model matemàtic que s'utilitza per descriure o predir grosso modo el seu estat o les seves propietats. Actualment no existeix una equació que permeti predir de manera acurada les propietats de qualsevol gas sota qualsevol situació. Per tant, hi ha una certa quantitat d'equacions d'estat que han estat desenvolupades per gasos amb intervals específics de pressió i temperatura. L'estat d'un gas està determinat per tres propietats: la seva pressió, el seu volum i la seva temperatura. Aquestes propietats estan relacionades de manera que imposant-ne dues la tercera queda determinada, l'equació que les relaciona és una equació d'estat o llei del gas, existeixen diferents models (aproximacions) que s'utilitzen habitualment, per exemple podem parlar dels models del gas ideal, del gas real, etc. Cadascuna d'aquestes aproximacions té el seu propi conjunt d'assumpcions per tal de facilitar l'anàlisi d'un determinat sistema termodinàmic.
Gas ideal
[modifica]En una primera aproximació, els gasos compleixen la llei dels gasos ideals, un gas ideal és aquell al que les forces intermoleculars són negligibles a causa de la separació entre les molècules i al que les col·lisions entre partícules són elàstiques. Aquest model també considera que el gas és constituït per àtoms (considerats com a partícules puntuals), que es mouen lliures de qualsevol força d'atracció o repulsió entre elles i les parets del recipient. La llei dels gasos ideals descriu, en condicions d'equilibri termodinàmic, la relació entre pressió, volum i temperatura del gas, l'equació d'estat d'aquest model és:
on P és la pressió, V és el volum que ocupa el gas, n és el nombre de mols de gas i T és la temperatura donada en kèlvins i R és una constant (constant dels gasos) que dependrà de les unitats que estem utilitzant. Els valors més habituals de R són 0,082 atm·l/mol·K i 8.314 J/mol·K. Per exemple, un mol de gas perfecte ocuparia 22,4 litres a una temperatura de 0 °C i una pressió d'1 atmosfera (uns 101.325 pascal)
D'aquesta llei se'n deriven la llei de Boyle o la de Charles i Gay-Lussac.
Llei de Boyle
[modifica]La llei de Boyle estableix que per una certa massa de gas a una temperatura T constant, el producte del volum V per la pressió P és constant:
O dit d'una altra manera, per una certa massa de gas a temperatura constant, les pressions són inversament proporcionals als volums.
La figura geomètrica que genera l'equació anterior és una hipèrbola equilàtera. La llei de Boyle és una bona aproximació, però no és vàlida per a tots els gasos. No existeix un gas ideal que segueixi perfectament la llei de Boyle. Però les desviacions del comportament dels gasos reals són molt petites per a un gas a baixa pressió i a una temperatura llunyana a la de liqüefacció. La transformació isotèrmica és per tant un canvi del volum i de la pressió mantenint constant la temperatura.
Llei de Charles i Gay-Lussac
[modifica]La llei de Charles i Gay-Lussac estableix que en condicions de pressió constant, el volum d'una massa coneguda de gas augmenta o disminueix proporcionalment a l'augment o disminució de la seva temperatura.
on és el volum ocupat pel gas a 0 °C i és igual a 1/273,15.
El procés isobàric és una variació del volum i de la temperatura a pressió constant, en un diagrama pressió-volum seria representat per un segment paral·lel a l'eix de volums. El canvi de volum que experimenta un gas per cada grau celsius de temperatura és d'1/273 del volum que ocupa el gas a 0 °C.
Segona llei de Gay-Lussac
[modifica]La segona llei de Gay-Lussac estableix que la relació entre la pressió i el volum és la mateixa que la que hi ha entre la temperatura i el volum, de manera que podrem conèixer la relació entre la pressió d'un gas i la seva temperatura quan el volum és constant. Un gas ideal a la temperatura de 0 °C tindrà una pressió P0, si l'escalfem mantenint constant el volum tindrem que a la temperatura T:
El procés isocòric és una variació de la pressió i de la temperatura mantenint un volum constant.
A més de les lleis mencionades, també seria vàlida per a un gas ideal la llei d'Avogadro , que estableix que en condicions iguals de pressió i temperatura, si dos gasos ocupen el mateix volum llavors ambdós tindran el mateix nombre de molècules. O dit d'una altra manera, si la pressió i la temperatura són constants el volum del gas és proporcional al nombre de molècules.
Gas real
[modifica]Cadascuna de les assumpcions que se citen més avall afegeix complexitat a la solució del problema. A mesura que s'incrementa la densitat d'un gas amb l'augment de la pressió, les forces intermoleculars tenen un paper més important en el comportament del gas de manera que la llei dels gasos ideals deixa de proporcionar resultats raonables. A l'extrem superior de les temperatures d'un motor (per exemple, 1.300 K al combustor d'una turbina de gas), les partícules del combustible absorbeixen energia interna, el que significa que varia el seu calor específic i en conseqüència les vibracions i rotacions que causa són diferents del que s'observa a les molècules diatòmiques i els gasos nobles. A més del doble d'aquesta temperatura comença l'excitació electrònica i la dissociació de les partícules del gas causant un ajustament de la pressió a causa de l'augment del nombre de partícules. S'espera que tots els processos termodinàmics descriguin gasos uniformes on les velocitats de les partícules varien d'acord amb una distribució fixa. Una situació de no equilibri implica que el flux s'ha de caracteritzar d'alguna manera per tal d'arribar a alguna solució, un dels primers intents per ampliar els límits de la llei dels gasos ideals fou la inclusió de la cobertura per a diferents processos termodinàmics ajustant l'equació per considerar i llavors anar variant amb diferents valors com el coeficient de dilatació adiabàtica, γ.
- Els ajustaments que es poden fer per ampliar la cobertura del comportament dels gasos reals inclouen:
- Factor de compressibilitat (permetent que Z sigui diferent d'1,0)
- Capacitància tèrmica variable
- Forces de van der Waals (relacionades amb la compressibilitat)
- Termodinàmica del no equilibri
- Problemes amb dissociacions moleculars i reaccions elementals amb una composició variable.
La llei dels gasos ideals prediu que una quantitat donada de gas ocupara un volum cada vegada més gran, a mesura que es redueix la pressió. Però, en realitat, els gasos reals no s'expandeixen infinitament, sinó que arribaria un moment en el qual no ocuparien més volum. Això és a causa del fet que entre els seus àtoms o molècules s'estableixen unes forces bastant petites, degut als canvis aleatoris de les seves càrregues electroestàtiques, a les quals se'ls anomena forces de Van der Waals.
Aquestes forces d'atracció i altres aspectes, com el volum que ocupa la mateixa molècula o àtom, es tenen en compte en models millorats de gasos. Un exemple és l'equació del gas de Van der Waals: , on s'afegeixen els paràmetres a i b que són propis de cada gas. El paràmetre b és una estimació del volum d'un mol de partícules (en l'estat més comprimit possible).
Per a moltes aplicacions una anàlisi tan detallada és excessiva, un exemple o els efectes dels gasos reals tenen un impacte significatiu que cal tenir en consideració seria per exemple la reentrada a l'atmosfera de naus com els transbordadors espacials o una erupció volcànica, en tots dos casos ens trobem amb gasos a temperatures i pressions extremadament altes.
Altres conceptes
[modifica]Compressibilitat
[modifica]
En termodinàmica s'utilitza el factor de compressibilitat () per modificar l'equació d'estat d'un gas ideal per tenir en compte els efectes de compressibilitat dels gasos reals. Aquest factor representa la relació entre els volum específic real i l'ideal. De vegades s'utilitza per ampliar els límits de validesa o utilitat de la llei dels gasos ideals per a fins de disseny. Habitualment és un valor molt proper a la unitat.
Nombre de Reynolds
[modifica]
En mecànica de fluids, el nombre de Reynolds és una relació entre les forces inercials (vsρ) i les de la viscositat (μ/L). És un dels nombres adimensionals més importants en dinàmica de fluids i s'acostuma a utilitzar conjuntament amb d'altres per tal d'establir un criteri per determinar la similitud dinàmica. Aquest nombre proporciona un vincle entre els resultats d'un model i els que se n'obtindrien a escala real. També pot ser utilitzat per caracteritzar un flux.
Viscositat
[modifica]La viscositat és una propietat física de la matèria, una mesura de la resistència que presenta un material a fluir. Dit d'una altra manera, és una mesura de les forces intermoleculars que tendeixen a mantenir unides les molècules amb les adjacents. Un sòlid pot suportar grans forces perquè les forces intermoleculars són molt fortes. Un fluid, en canvi es deforma contínuament quan se'l sotmet a una força. Tot i que els gasos tenen un valor de viscositat més petit que els líquids encara és prou gran per ser observable.
Turbulència
[modifica]En dinàmica de fluids, una flux turbulent és un tipus de flux que es caracteritza per canvis de tipus caòtic o aleatori. Es caracteritzen per un petit moment de difusió, un alt moment de convecció i una ràpida variació de la pressió i la temperatura en l'espai i el temps. La turbulència que mostra la imatge de la dreta és coneguda com a vòrtex de von Karman i és una successió de vòrtex.
Equilibri termodinàmic
[modifica]Quan a un sistema no hi ha transferència d'energia direm que està en equilibri termodinàmic. Habitualment això implica que el sistema i el medi que l'envolta són a la mateixa temperatura de manera que no hi ha transferència de calor entre ambdós. Això també implica que les forces externes són en equilibri (el volum no canvia), i que totes les reaccions químiques a l'interior del sistema han finalitzat. El temps requerit per arribar a una situació d'equilibri termodinàmic varia en funció del sistema, per exemple, un contenidor amb gel fonent-se a la temperatura ambient d'una habitació pot trigar hores a arribar-hi mentre que a un semiconductor la transferència de calor que es produeix durant la transició d'un estat a un altre es pot produir en pocs nanosegons.
Referències
[modifica]- ↑ Concept Development Studies in Chemistry, John S. Hutchinson. (2008).
- ↑ lắp đặt hệ thống gas (en vietnamita). anmy.
- ↑ John D. Anderson's Fundamentals of Aerodynamics (1984). ISBN 0-07-001656-9
Vegeu també
[modifica]- Canvi d'estat
- Fase de la matèria
- Llei de Graham
- Núvol
- Olfacte
- Olor
- Teoria cinètica molecular
- Vapor
- Vent
- Articles dintre de la categoria Gasos
Bibliografia complementària
[modifica]- John D. Anderson. Modern Compressible Flow: Third Edition Nova York, NY : McGraw-Hill, 2004. ISBN 0-07-124136-1
- Philip Hill and Carl Peterson. Mechanics and Thermodynamics of Propulsion: Second Edition Addison-Wesley, 1992. ISBN 0-201-14659-2
- John D. Anderson. Fundamentals of Aerodynamics: Fourth Edition Nova York, NY : McGraw-Hill, 2007. ISBN 978-0-07-295046-5 ISBN 0-07-295046-3
- National Aeronautics and Space Administration (NASA). Animated Gas Lab Arxivat 2010-11-22 a Wayback Machine.. (en anglès) Consultat el febrer del 2008.
- Georgia State University. HyperPhysics. (en anglès) Consultat el febrer del 2008.
- Antony Lewis WordWeb. (en anglès) Consultat el febrer del 2008.
- Northwestern Michigan College The Gaseous State Arxivat 2008-12-17 a Wayback Machine.. (en anglès) Consultat el febrer del 2008.












