Màquina de Turing


La màquina de Turing és un model computacional introduït per Alan Turing en el treball "On computable numbers, with an application to the Entscheidungsproblem", publicat per la Societat Matemàtica de Londres, en el qual s'estudiava la qüestió plantejada per David Hilbert sobre si les matemàtiques són decidibles, és a dir, si hi ha un mètode definit que pugui aplicar-se a qualsevol sentència matemàtica i que resolgui si és certa o no. Turing va construir un model formal de computador, la màquina de Turing, un dispositiu que manipula símbols sobre una tira de cinta d'acord amb una taula de regles i va demostrar que existien problemes que una màquina no podia resoldre.[1][2]
Malgrat la seva simplicitat, la màquina de Turing pot ser adaptada per simular la lògica de qualsevol algorisme de computador i és particularment útil en l'explicació de les funcions d'una CPU dins d'un computador.
Originalment va ser definida com una «màquina automàtica» el 1936, a la revista Proceedings of the Societat Mathematics[3] de Londres. La màquina de Turing no està dissenyada com una tecnologia de computació pràctica, sinó com un dispositiu hipotètic que representa una màquina de computació, i van ajudar als científics a entendre els límits del càlcul mecànic.
Turing va donar una definició succinta de l'experiment en el seu assaig de 1948, «Màquines intel·ligents». Referint-se a la seva publicació de 1936, Turing va escriure que la màquina de Turing, aquí anomenada una màquina de computació lògica, consistia en:
| « | ... una il·limitada capacitat de memòria obtinguda en la forma d'una cinta infinita marcada amb quadrats, en cadascun dels quals podria imprimir-se un símbol. En qualsevol moment hi ha un símbol a la màquina; anomenat el símbol llegit. La màquina pot alterar el símbol llegit i el seu comportament està en part determinat per aquest símbol, però els símbols en altres llocs de la cinta no afecten el comportament de la màquina. Tanmateix, la cinta es pot moure cap endavant i cap enrere a través de la màquina, essent això una de les operacions elementals de la màquina. Per tant qualsevol símbol a la cinta pot tenir finalment una oportunitat.[4] | » |
| — Turing (1948, p. 61.) | ||
Una màquina de Turing que sigui capaç de simular qualsevol altra màquina de Turing és anomenada com una màquina universal de Turing (UTM, o simplement una màquina universal). Una definició més matemàticament orientada, amb una semblant naturalesa "universal", va ser presentada per Alonzo Church, el treball sobre el càlcul lambda s'entrellaça amb el de Turing en una teoria formal de la computació coneguda com la tesi de Church-Turing. La tesi assenyala que les màquines de Turing capturen, de fet, la noció informal d'un mètode eficaç en la lògica i les matemàtiques i proporcionen una definició precisa d'un algoritme o 'procediment mecànic'.
Estudiant les seves propietats abstractes, la màquina de Turing produeix moltes perspectives en les ciències de la computació i en la teoria de la complexitat.
Història[modifica]
Alan Turing va introduir el concepte de màquina de Turing a l'article On computable numbers, with an application to the Entscheidungsproblem, publicat per la Societat Matemàtica de Londres el 1936, en el qual s'estudiava la qüestió plantejada per David Hilbert sobre si les matemàtiques són decidibles.
Mitjançant aquest model teòric i l'anàlisi de la complexitat dels algoritmes, va ser possible la categorització de problemes computacionals d'acord amb el seu comportament, apareixent així, el conjunt de problemes denominats P i NP, les solucions poden trobar-se en temps polinòmic per màquines de Turing deterministes i no deterministes, respectivament.
Precisament, la tesi de Church-Turing formulada per Alan Turing i Alonzo Church, de forma independent a mitjan segle xx caracteritza la noció informal de computabilitat amb la computació mitjançant una màquina de Turing.[5]
La idea subjacent és el concepte que una màquina de Turing pot veure com un autòmat executant un procediment efectiu definit formalment, on l'espai de memòria de treball és il·limitat, però en un moment determinat només una part finita accessible.
Descripció[modifica]

La màquina de Turing modela matemàticament a una màquina que opera mecànicament sobre una cinta. En aquesta cinta hi ha símbols que la màquina pot llegir i escriure, un alhora, usant un capçal lector / escriptor de cinta. L'operació està completament determinada per un conjunt finit d'instruccions elementals com "en l'estat 42, si el símbol vist és 0, escriu un 1; Si el símbol vist és 1, canvia a l'estat 17, en l'estat 17, si el símbol vist és 0, escriu un 1 i canvia l'estat 6; etc ". En l'article original ("Sobre nombres computables amb una aplicació al Entscheidungsproblem"), Turing no s'imagina un mecanisme, sinó una persona a qui ell anomena la "ordinador", qui executa servilment aquestes regles mecàniques deterministes (o com Turing posa, "d'una manera desganada").
Més precisament, una màquina de Turing consta de:
- Una cinta que es divideix en cel·les, una al costat de l'altra. Cada cel·la conté un símbol d'algun alfabet finit. L'alfabet conté un símbol especial anomenat blanc (aquí escrit com 'B') i un o més símbols addicionals. La cinta se suposa que és arbitràriament extensible cap a l'esquerra i cap a la dreta, és a dir, la màquina de Turing sempre és subministrada amb tanta cinta com necessiti per a la seva computació. Les cel·les que no s'hagin escrit prèviament s'assumeixen que estan farcides amb el símbol blanc. En alguns models la cinta té un extrem esquerre marcat amb un símbol especial; la cinta s'estén o és indefinidament extensible a la dreta.
- Un capçal que pot llegir i escriure símbols en la cinta i moure la cinta a l'esquerra i a la dreta una (i només una) cel·la alhora. En alguns models el capçal es mou i la cinta és estacionària.
- Un registre d'estat que emmagatzema l'estat de la màquina de Turing, un dels estats finits. Hi ha un estat inicial especial amb el qual el registre d'estat s'inicia. Turing escriu que aquests estats reemplacen l'"estat de la ment" en què ordinàriament estaria una persona realitzant càlculs.
- Una taula finita d'instruccions (anomenada ocasionalment com a taula d'acció o funció de transició). Les instruccions són usualment 5-tuples: qiaj → qi1aj1dk, (de vegades 4-tuples), que, donat l'estat (qi) en què la màquina es troba actualment i el símbol (aj) que s'està llegint a la cinta (el símbol actualment sota del capçal) li indica a la màquina fer el següent en seqüència (per als models de 5-tupla):
- Esborra o escriu un símbol
- Mou el capçal
- Asumeix el mateix o un nou estat como preescrit. En els models de 4-tupla, són especificades com instruccions separades: esborrar o escriure un símbol (AJ1) i moure el capçal a l'esquerra o la dreta (dk). Específicament, la taula indica a la màquina: (ia) esborrar o escriure un símbol o (ib) moure el capçal a l'esquerra oa la dreta, i després (ii) assumir el mateix o un nou estat, però no les dues accions (ia) i (ib) en la mateixa instrucció. En alguns models, si no hi ha entrades a la taula per a l'actual combinació de símbol i estat, la màquina s'aturarà; altres models requereixen que estiguin plenes totes les entrades. Noti que cada part de la màquina - el seu estat i col·leccions de símbols - i les seves accions - imprimir, esborrar, moviment de la cinta - és finit, discret i distingible; és la quantitat potencialment il·limitada de cinta el que li dona una quantitat il·limitada d'espai d'emmagatzematge.
Les operacions que es poden realitzar en aquesta màquina es limiten a:
- avançar el capçal lector/escriptor cap a la dreta;
- avançar el capçal lector/escriptor cap a l'esquerra;
El còmput és determinat a partir d'una taula d'estats de la forma:
(estat, valor) (\nou estat, \nou valor, direcció)
Aquesta taula pren com a paràmetre l'estat actual de la màquina i el caràcter llegit de la cinta, donant la direcció per a moure el capçal, el nou estat de la màquina i el valor a ser escrit en la cinta.
Amb aquest aparell extremadament senzill és possible realitzar qualsevol còmput que un computador digital sigui capaç de realitzar.
Mitjançant aquest model teòric i l'anàlisi de complexitat d'algorismes, va ser possible la categorització de problemes computacionals d'acord amb el seu comportament, apareixent així, el conjunt de problemes denominats P i NP, les solucions dels quals en temps polinòmic són trobades segons el determinisme i no determinisme respectivament de la màquina de Turing.
De fet, es pot provar matemàticament que per a qualsevol programa de computador és possible crear una màquina de Turing equivalent. Aquesta prova resulta de la Tesi de Church-Turing, formulada per Alan Turing i Alonzo Church de forma independent a mitjans del segle xx.
La idea subjacent en el concepte de màquina de Turing és una persona executant un procediment efectiu definit formalment, on l'espai de memòria de treball és il·limitat, però en un moment determinat només una part finita és accessible. La memòria es divideix en espais de treball denominades cel·les, on es pot llegir i escriure símbols. Inicialment totes les cel·les contenen un símbol especial denominat "blanc". Les instruccions que determinen el funcionament de la màquina tenen la forma, "si estem en l'estat x llegint la posició y, on hi ha escrit el símbol z, llavors aquest símbol ha de ser reemplaçat per aquest altre símbol, i passar a llegir la cel·la següent, bé a l'esquerra bé a la dreta". La màquina de Turing pot considerar-se com un autòmat capaç de reconèixer llenguatges formals. En aquest sentit, és capaç de reconèixer els llenguatges recursivament enumerables, d'acord amb la jerarquia de Chomsky. La seva potència és, per tant, superior a altres tipus d'autòmats, com l'autòmat finit, o l'autòmat amb pila, o igual a altres models amb la mateixa potència computacional.
Definició[modifica]
Una màquina de Turing[6] és un model computacional que realitza una lectura / escriptura de manera automàtica sobre una entrada anomenada cinta, generant una sortida en aquesta mateixa.
Aquest model està format per un alfabet d'entrada i un de sortida, un símbol especial anomenat blanc, un conjunt d'estats finits i un conjunt de transicions entre aquests estats. El seu funcionament es basa en una funció de transició, que rep un estat inicial i una cadena de caràcters (la cinta, la qual pot ser infinita) pertanyents a l'alfabet d'entrada. La màquina va llegint una cel·la de la cinta a cada pas, esborrant el símbol en què es troba posicionat seu capçal i escrivint un nou símbol que pertany a l'alfabet de sortida, per després desplaçar el capçal a l'esquerra oa la dreta (només una cel·la alhora). Això es repeteix segons s'indiqui en la funció de transició, per finalment aturar-se en un estat final o d'acceptació, representant així la sortida.
Una màquina de Turing amb una sola cinta pot ser definida com una 7-tupla:

, on:[7]
- és un conjunt finit d'estats
- és un conjunt finits de símbols de cinta, l'alfabet de cinta
- és l'estat inicial
- és un símbol denominat blanc, i és l'únic símbol que es pot repetir un nombre infinit de cops
- és el conjunt d'estats finals d'acceptació
- és una funció parcial denominada funció de transició, on L és un moviment a l'esquerra i R és el moviment a la dreta.
Existeix a la literatura un abundant nombre de definicions alternatives, però totes elles tenen el mateix poder computacional, per exemple es pot afegir el símbol S com símbol de "no moviment" en un pas de còmput.
Funcionament[modifica]
La màquina de Turing consta d'un capçal lector / escriptor i una cinta infinita en la qual el capçal llegeix el contingut, esborra el contingut anterior i escriu un nou valor. Les operacions que es poden realitzar en aquesta màquina es limiten a:
- Moure el capçal lector / escriptor cap a la dreta.
- Moure el capçal lector / escriptor cap a l'esquerra.

El còmput es determina a partir d'una taula d'estats de la forma:
- (estat, valor) (nou estat, nou valor, direcció)
Aquesta taula pren com a paràmetres l'estat actual de la màquina i el caràcter llegit de la cinta, donant la direcció per moure el capçal, el nou estat de la màquina i el valor a escriure a la cinta.
La memòria és la cinta de la màquina que es divideix en espais de treball denominats cel·les, on es poden escriure i llegir símbols. Inicialment totes les cel·les contenen un símbol especial denominat "blanc". Les instruccions que determinen el funcionament de la màquina tenen la forma, "si estem en l'estat x llegint la posició i, on hi ha escrit el símbol z, llavors aquest símbol ha de ser reemplaçat per aquest altre símbol, i passar a llegir la cel·la següent, bé a l'esquerra o bé a la dreta".
La màquina de Turing pot considerar-se com un autòmat capaç de reconèixer llenguatges formals. En aquest sentit, és capaç de reconèixer els llenguatges recursivament enumerables, d'acord amb la jerarquia de Chomsky. La seva potència és, per tant, superior a altres tipus d'autòmats, com l'autòmat finit, o l'autòmat amb piles, o igual a altres models amb la mateixa potència computacional.
Representació com a diagrama d'estats[modifica]
Les màquines de Turing poden representar-se mitjançant grafs particulars, també anomenats diagrames d'estats finits, de la següent manera:
- , posseeix el conjunt d'estats
- , amb les transicions que es poden veure. El seu estat incial és i el seu estat final és , el llenguatge de sortida
- sent el símbol denominat "blanc". Aquesta màquina reconeix l'expressió regular de la forma con .
- Els estats es representen com a vèrtexs, etiquetats amb el seu nom a l'interior.
- Una transició des d'un estat a un altre, es representa mitjançant una aresta dirigida que uneix aquests vèrtexs, i està retolada pel símbol que llegeix el capçal/símbol que escriurà el capçal, moviment del capçal.
- L'estat inicial es caracteritza per tenir una aresta que arriba a ell i que no prové de cap altre vèrtex.
- El o els estats finals es representen mitjançant vèrtexs que estan tancats al seu torn per una altra circumferència.
Descripció instantània[modifica]
És una seqüència de la forma on i que escriu l'estat d'una MT. La cinta conté la cadena seguida d'infinits blancs. El capçal senyala el primer símbol de .
Per exemple, per a la màquina de Turing
amb les transicions
La descripció instantània per a la cinta 1011 és:
Exemple[modifica]
Definim una màquina de Turing sobre l'alfabet , on 0 representa el símbol blanc. La màquina començarà el seu procés situada sobre un símbol "1" d'una sèrie. La màquina de Turing copiarà el nombre de símbols "1" que trobi fins al primer blanc darrere d'aquest símbol blanc. És a dir, posiciona el capçal sobre l'1 situat a l'extrem esquerre, doblarà el nombre de símbols 1, amb un 0 al mig. Així, si tenim l'entrada "111" tornarà "1.110.111", amb "1111" tornarà "111.101.111", i successivament.
El conjunt d'estats és i l'estat inicial és . La taula que descriu la funció és la següent:
| Estat | Símbol llegit | Símbol escrit | Mov. | Estat seg. |
|---|---|---|---|---|
| 1 | 0 | |||
| 1 | 1 | |||
| 0 | 0 | |||
| 0 | 1 | |||
| 1 | 1 | |||
| 1 | 1 | |||
| 0 | 0 | |||
| 1 | 1 | |||
| 0 | 1 |
El funcionament d'una computació d'aquesta màquina pot mostrar-se amb el següent exemple (en negreta es ressalta la posició del cap lector / escriptora):
| Pas | Estat | Cinta |
|---|---|---|
| 1 | 11 | |
| 2 | 01 | |
| 3 | 010 | |
| 4 | 0100 | |
| 5 | 0101 | |
| 6 | 0101 | |
| 7 | 0101 | |
| 8 | 1101 | |
| 9 | 1001 | |
| 10 | 1001 | |
| 11 | 10010 | |
| 12 | 10011 | |
| 13 | 10011 | |
| 14 | 10011 | |
| 15 | 11011 | |
| Parada | ||
La màquina realitza el seu procés per mitjà d'un bucle, en l'estat inicial , reemplaça el primer 1 amb un 0, i passa a l'estat , amb el que avança cap a la dreta, saltant els símbols 1 fins a un 0 (que ha d'existir), quan el troba passa a l'estat , amb aquest estat avança saltant als 1 fins a trobar un altre 0 (la primera vegada no hi haurà cap 1). Un cop a l'extrem dret, afegeix un 1. Després comença el procés de retorn; amb torna a l'esquerra saltant els 1, quan troba un 0 (en el mitjà de la seqüència), passa a que continua a l'esquerra saltant als 1 fins al 0 que es va escriure al principi. Es reemplaça de nou aquest 0 per 1, i passa al símbol següent, si és un 1, es passa a una altra iteració del bucle, passant a l'estat s1 de nou. Si és un símbol 0, serà el símbol central, amb el que la màquina s'atura en haver finalitzat el còmput.
Modificacions equivalents[modifica]

Una raó per acceptar la màquina de Turing com un model general de còmput és que el model que hem definit anteriorment és equivalent a moltes versions modificades que en principi semblés incrementar el poder computacional.
Màquina de Turing amb moviment stay o "esperar"[modifica]
La funció de transició de la MT senzilla està definida per:
que pot ser modificada com:
on vol dir "esperar", és a dir, no moure el capçal de lectura/escriptura. Per tant, vol dir que es passa de l'estat q al p, s'escriu a la cel·la actual i el cap queda sobre la cel·la actual.

Màquina de Turing amb cinta infinita pels dos costats[modifica]
Aquesta modificació es denota la mateixa manera que una MT senzilla, el que la fa diferent és que la cinta és infinita tant per la dreta com per l'esquerra, la qual cosa permet realitzar transicions inicials com .
Màquina de Turing amb cinta multipista[modifica]
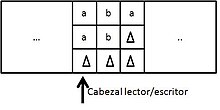
És aquella que mitjançant la qual cada cel·la de la cinta d'una màquina senzilla es divideix en subcel·les. Cada cel·la és així capaç de contenir diversos símbols de la cinta. Per exemple, la cinta de la figura té cada cel·la subdividida en tres subcel·les.
Es diu que aquesta cinta té múltiples pistes ja que cada cel·la d'aquesta màquina de Turing conté múltiples caràcters, el contingut de les cel·les de la cinta pot ser representat mitjançant n-tuples ordenades. Els moviments que realitzi aquesta màquina dependran del seu estat actual i de la n-tupla que representi el contingut de la cel·la actual. Cal esmentar que posseeix un sol capçal de la mateixa manera que una MT senzilla.

Màquina de Turing multicinta[modifica]
Una MT amb més d'una cinta consisteix d'un control finit amb k capçals lectors / escriptors i k cintes. Cada cinta és infinita en tots dos sentits. La MT defineix el seu moviment depenent del símbol que està llegint cadascun dels seus capçals, dona regles de substitució per a cada un dels símbols i direcció de moviment per a cada un dels capçals. Inicialment la MT comença amb l'entrada en la primera cinta i la resta de les cintes en blanc.
Màquina de Turing multidimensional[modifica]
Una MT multidimensional és aquella la cinta es pot veure com estenent infinitament en més d'una direcció, l'exemple més bàsic seria el d'una màquina bidimensional la cinta s'estendria infinitament cap amunt, avall, dreta i esquerra.
En la modificació bidimensional de MT que es mostra a la figura també s'agreguen dos nous moviments del capçal {U, D} (és a dir amunt i avall). D'aquesta forma la definició dels moviments que realitza el capçal serà {L, R, U, D}.
Màquines de Turing deterministes i no deterministes[modifica]
L'entrada d'una Màquina de Turing ve determinada per l'estat actual i el símbol llegit, sent el canvi d'estat, l'escriptura d'un nou símbol i el moviment les accions a prendre en funció d'una entrada. En el cas que per a cada parell d'estat i símbol possible existeixi com a molt una possibilitat d'execució, direm que és una màquina de Turing determinista, mentre que en el cas que existeixin almenys un parell (estat, símbol) amb més d'una possible combinació d'actuacions direm que es tracta d'una màquina de Turing no determinista.
La funció de transició en el cas no determinista queda definida com segueix:
Com sap una màquina no determinista quina acció prendre de les diverses possibles? Hi ha dues maneres de veure-ho: una és a dir que la màquina és "el millor endeví possible", això és, que només utilitza la transició que finalment la portarà a un estat final d'acceptació. L'altra és imaginar-se que la màquina es "clona", bifurcant-se en diverses còpies, cadascuna de les quals segueix una de les possibles transicions. Mentre que una màquina determinista segueix un únic "camí computacional", una màquina no determinista té un "arbre computacional". Si qualsevol de les branques de l'arbre finalitza en un estat d'acceptació, es diu que la màquina accepta l'entrada.
La capacitat de còmput d'ambdues màquines és equivalent; es pot demostrar que donada una màquina de Turing no determinista existeix una màquina de Turing determinista equivalent, en el sentit que reconeixen el mateix llenguatge, i viceversa. Tanmateix, la velocitat d'execució d'ambdós formalismes no és la mateixa, ja que una màquina no determinista M reconeix una certa paraula de mida n en un temps , la màquina determinista equivalent reconeixerà la mateixa paraula en un temps . És a dir, el no determinisme permetrà reduir la complexitat temporal de la solució dels problemes, permetent resoldre, per exemple, problemes de complexitat exponencial en un temps polinòmic.
Problema de la parada (halting problem)[modifica]
El problema de l'aturada o problema de la detenció (halting problem en anglès) per a màquines de Turing consisteix en: donada una MT M i una paraula w, determinar si M acabarà en un nombre finit de passos quan s'executa usant w com a entrada.
Alan Turing, en el seu famós article «On computable numbers, with an application to the Entscheidungsproblem» (1936), va demostrar que el problema de la parada de la màquina de Turing és indecidible, en el sentit que cap màquina de Turing ho pot resoldre.[8]
Codificació d'una màquina de Turing[modifica]
Tota màquina de Turing pot codificar-se com una seqüència binària finita, és a dir, una seqüència finita de ceros i uns. Per simplificar la codificació, suposem que tota MT té un únic estat inicial denotat per , i un únic estat final denotat per . Para una MT M de la forma:
- on representa el símbol blanc 0, o b (segons es vulgui denotar),
- és alfabet d'entrada i
- són els símbols auxiliars utilitzats per M (cada MT utilitza la seva col·lecció finita de símbols auxiliars).
Tots aquests símbols es codifiquen com seqüències d'uns:
| Símbol | Codificació |
|---|---|
| 1 | |
| 11 | |
| 111 | |
| . . . |
. . . |
Els estats d'una MT es codifiquen també com a seqüències d'uns:
| Símbol | Codificació |
|---|---|
| 1 | |
| 11 | |
| . . . |
. . . |
Les directrius de desplaçament , i es codifiquen com 1, 11, 11, respectivament. Una transició es codifica fent servir zeros com a separadors entre els estats, els símbols de l'alfabet de la cinta i la directriu de desplaçament . Així, la transició es codifica com:
En general, la codificació d'una transició qualsevol és:
on , segon la direcció sigui .
Una MT es codifica escrivint consecutivament les seqüències de les modificacions de totes les seves transicions. Més precisament, la codificació d'una MT M és de la forma , on és la codificació de la -ésima transició de M. Com que l'ordre en què es representen les transicions d'una MT no és rellevant, una mateixa MT té diverses codificacions diferents. Això no representa cap desavantatge pràctica o conceptual, ja que no es pretén que les codificacions siguin úniques
Màquina universal de Turing[modifica]
Una màquina de Turing computa una determinada funció parcial de caràcter definit i unívoca, definida sobre les seqüències de possibles cadenes de símbols del seu alfabet. En aquest sentit es pot considerar com equivalent a un programa informàtic o, cosa que és el mateix, a un algorisme. Tanmateix, és possible realitzar una codificació de la taula que representa a una màquina de Turing com una seqüència de símbols en un determinat alfabet; per això, podem construir una màquina de Turing que accepti com entrada la taula que representa a una altra màquina de Turing i que simuli el seu comportament.
| « | Es pot demostrar que és possible construir una màquina especial d'aquest tipus que pugui realitzar el treball de totes les altres. Es podria fer que treballés com a model d'altres màquines. Aquesta màquina especial es pot denominar màquina universal. | » |
Aquesta fou possiblement, la idea germinal del concepte de sistema operatiu,[9] un programa que pot executar altres programes i controlar-los, demostrant la seva existència i obrint camí per la seva construcció real.
Amb aquesta codificació de taules com a cadenes, s'obre la possibilitat que una màquina de Turing es comporti com altres màquines de Turing. Tanmateix, moltes de les seves possibilitats són indecidibles, perquè no admeten una solució algorísmica. Per exemple, un interessant problema és determinar si una màquina de Turing qualsevol pararà en un temps finit sobre una determinada entrada; aquest problema és conegut com el problema de la parada, i que Turing va demostrar que era indecidible. En general, es pot demostrar que qualsevol qüestió no trivial sobre el comportament o la sortida d'una màquina de Turing és un problema indecidible.
Màquina quàntica de Turing[modifica]
En 1985, Deutsch va presentar el disseny de la primera Màquina quàntica basada en una màquina de Turing. Amb aquesta finalitat va enunciar una nova variant la tesi de Church-Turing donant lloc al denominat "principi de Church-Turing-Deutsch".

L'estructura d'una màquina de Turing quàntica és molt similar a la d'una màquina de Turing clàssica. Està composta pels tres elements clàssics:
- Una cinta de memòria infinita on cada element és un qubit.
- Un processador finit.
- Un capçal.
El processador conté el conjunt d'instruccions que s'aplica sobre l'element de la cinta assenyalat pel capçal. El resultat dependrà del qubit de la cinta i de l'estat del processador. El processador executa una instrucció per unitat de temps.
La cinta de memòria és similar a la d'una màquina de Turing tradicional. L'única diferència és que cada element de la cinta de la màquina quàntica és un qubit. L'alfabet d'aquesta nova màquina està format per l'espai de valors del qubit. La posició del capçal es representa amb una variable sencera.
Referències[modifica]
- ↑ 1912-1954., Turing, Alan,. The essential Turing : seminal writings in computing, logic, philosophy, artificial intelligence, and artificial life, plus the secrets of Enigma. Oxford: Clarendon Press, 2004. ISBN 9780191520280.
- ↑ The undecidable : basic papers on undecidable propositions, unsolvable problems and computable functions. Dover ed. Mineola, N.Y.: Dover Publications, 2004. ISBN 0486432289.
- ↑ La idea la va tenir a mitjans de 1935 (vegeu més a la secció Història), després d'una pregunta de M. H. A. Newman a les seves classes. Turing va enviar el seu article el 31 de maig de 1936 a la London Mathematical Society per la seva publicació a la revista Proceedings (cf Hodges 1983:112), però no es va publicar fins a prinvipis de 1937.
- ↑ See the definition of "innings" on Wiktionary
- ↑ Introducción a la computación, 2008.
- ↑ «Teoría de Autómatas». Teoría de Autómatas, RAI 2012 Universidad Carlos III
- ↑ Pérez, Iván Lenguaje y Compiladores, 2005.
- ↑ Turing, A. M. «On Computable Numbers, with an Application to the Entscheidungsproblem» (en anglès). Proceedings of the London Mathematical Society, s2-42, 1, 1937, pàg. 230–265. Arxivat de l'original el 2019-06-27. DOI: 10.1112/plms/s2-42.1.230. ISSN: 1460-244X [Consulta: 23 desembre 2018].
- ↑ Membrane Computing: An Introduction. Springer-Verlag, 2002. ISBN 3540436014.
Vegeu també[modifica]
- Teorema d'invariància.
- Teoría d'autòmats
- Autòmat finit
- Problema de la parada
- Jerarquia de Chomsky
- Joc de la vida
- Càlcul lambda
Bibliografia[modifica]
- Feynman, Richard (1996). Conferencias sobre computación. Graficromo. ISBN 84-8432-444-3. Consultat l'11 de juliol de 2010.
- Viso, Elisa (2008). Introducción a la teoría de la computación. ISBN 978-970-32-5415-6. Consultat l'11 de juliol de 2010.
- De Castro, Rodrigo (2004). Teoría de la computación: lenguajes, autómatas, gramáticas. Consultat el 15 de juliol de 2010.
- «on computable numbers,with an application to the entscheidungsproblem» Arxivat 2011-02-22 a Wayback Machine.. Consultat el 15 de juliol de 2010.
- «Variantes de una Máquina de Turing». Archivado desde el originalArxivat 2011-11-26 a Wayback Machine. el 25 de novembre de 2015. Consultat l'11 de juliol de 2010.
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Màquina de Turing |
- Sitio web de Stephen Wolfram
- Demuestran que la máquina de Turing (2,3) es universal
- Màquina de Turing construïda sobre hardware
- Video de máquina de Turing mecánica en YouTube
- https://tricas.cat/turing Enllaç a un simulador màquina de Turing (Javascript)




















































































