Engranatge

S'anomena engranatge al sistema de rodes proveïdes de dents en la seva perifèria o amb dentat interior o lateral que, engrana amb les dents d'altres rodes dentades.[1] Es un element utilitzat per transmetre moviment entre les diferents parts d'una màquina o mecanisme mòbil. Els engranatges estan formats per dues o més rodes dentades. La més petita s'anomena pinyó. Un engranatge serveix per transmetre moviment circular mitjançant el contacte de rodes dentades. Si el sistema és compost de més d'un parell de rodes dentades, es pot anomenar tren d'engranatges, que estan construïts per rodes dentades.
Història[modifica]


Els primers exemples d'engranatges daten del segle iv aC a la Xina[2] (època del Zhan Guo - Dinastia tardana del Zhou de l'est), que s'han conservat al Museu Luoyang de la província de Henan, Xina. Els primers engranatges conservats a Europa es van trobar en el mecanisme Antikythera, un exemple d'un dispositiu enginyós molt primitiu i complicat, dissenyat per calcular posicions astronòmiques. El seu moment de construcció ara s'estima entre els anys 150 i 100 aC.[3] Els engranatges apareixen en obres connectades a Heró d'Alexandria, a l'Egipte romà al voltant de l'any 50,[4] però es poden remuntar a la mecànica de l'escola d'Alexandria del segle iii aC per part de Ptolemeu i van ser molt desenvolupats pel polímata grec Arquimedes (287-212 aC).[5]
L'enginy segmental, que rep/comunica moviment alternatiu des de i cap a una roda dentada, que consisteix en un sector d'engranatge circular que té engranatges a la perifèria,[6] va ser inventat per l'enginyer àrab Al-Jazari el 1206.[7] El vis-sens-fi va ser inventat en el subcontinent indi, per a ús en ginys de cotó de rodets, al voltant dels segles XIII-XIV.[8] Es poden haver usat engranatges diferencials en alguns dels carros xinesos que apunten sempre al sud,[9] però fou el fabricant de rellotges britànic Joseph Williamson, el 1750, qui va fer el primer ús verificable dels engranatges diferencials.
Exemples d'aplicacions d'engranatges primitius:
- El mecanisme d'Antikythera (segle ii aC)
- Ma Jun (aproximadament 200-265 dC) va utilitzar engranatges com a part d'un carro orientat al sud .
- Els primers rellotges mecànics orientats van ser construïts a la Xina a l'any 725.
- Al-Jazari (devers 1206) va inventar l'engranatge segmentari com a part d'un dispositiu d'elevació d'aigua.[7]
- El vis sens fi va ser inventat com a part d'una desmotadora de cotó en el subcontinent indi (segles xiii-xiv).[8]
- El rellotge 1386 de la catedral de Salisbury pot ser el rellotge mecànic documentat més antic del món, encara en funcionament.
Cronologia[modifica]
- Devers 1600. L'astrònom Johannes Kepler inventà la bomba d'engranatges. Encara molt usada actualment com a bomba d'oli en la lubricació de motors.[10]
- 1673. Perfil cicloïdal proposat per Christiaan Huygens.[11]
- 1911. Primera aplicació del sistema d'acabament per afaitat.[12]
- 1957. Patent del sistema d'engranatge harmònic.[13][14]
Tipus de dents[modifica]
Les rodes dentades poden ser dissenyades i fabricades amb dents de diversos perfils. Els perfils més importants són els següents:
- evolvent
- cicloïdal
- Wildhaber-Novikov.[15]
Tipus d'engranatges[modifica]
Els principals tipus d'engranatges són:
- 1. Engranatges rectes
- 2. Engranatges helicoidals
- 3. Vis sens fi
- 4. Pinyó-cremallera
- 5. Engranatges interiors
- 6. Engranatge epicicloïdal o planetari
- 7. Engranatges cònics. S'utilitzen bàsicament per transferir potència entre els eixos que s'intersequen. Els «normals» tenen les dents rectes i alineades paral·lelament a la línia que assenyala el con que generaria la figura. En canvi els engranatges cònics espirals tenen les seves dents formant línies corbes.
Identificació d'un engranatge[modifica]
Per identificar i calcular un engranatge, hi ha una sèrie de paràmetres que són comuns a tots ells:
- Modul= M = defineix la mida de la dent, i és determinant per la càrrega a transmetre.
- Nombre de dents= z =que relacionat amb el nombre de dents de la roda amb la que engrana determinarà la velocitat angular de cada una
- Diàmetre primitiu= Dp =és el diàmetre teòric on es produeix el contacte de les dents
- Diàmetre exterior= De = és el diàmetre de fora de l'engranatge
- Diàmetre interior= Di = és el diàmetre del fondo de les dents
- Alçària de la dent= h = en les dues rodes és menester que sigui igual
- Angle de pressió= α = és l'angle en què s'exerceix la pressió entre flancs. El més utilitzat és de 20º
- Espesor circular = e = és la longitud de l'arc de diàmetre primitiu que compren una dent, o un forat
- Pas= p = la suma de la distància cordal sobre el primitiu, d'una dent i el forat que ve a continuació
Característiques dels engranatges helicoidals[modifica]

Els engranatges helicoidals estan tallats en forma d'hèlix, d'on reben el seu nom. Pel seu tallat és necessari calcular les rodes de diferencial que donaran forma a la dent de l'engranatge.
Els engranatges helicoidals tenen l'avantatge que transmeten més potència que els engranatges rectes, ja que tenen més d'una dent en contacte, i també poden transmetre més velocitat, són més silenciosos i més duradors; a més a més, poden transmetre el moviment d'eixos que es tallen.
Com a inconvenient, produeixen esforços laterals, que s'absorbeixen amb coixinets cònics.
El pas (P) d'hèlice segons l'angle β ve donat per la següent expressió.[17]
Característiques d'un vis sens fi[modifica]

És un mecanisme dissenyat per a la transmissió de grans esforços, i com a reductors de velocitat, augmenten el parell transmès amb relacions de transmissió grans. Generalment treballen amb eixos que es tallen a 90°.
En l'engranament del vis sens fi hi ha velocitats elevades de lliscament relatiu entre les dents. Les pèrdues per fricció són doncs, elevades i això fa que la reducció de vis sens fi tingui un baix rendiment i una vida limitada pel desgast de les dents. En sentit invers el rendiment encara és menor fins i tot nul. En aquest cas la transmissió és irreversible. La irreversibilitat del vis sens fi s'empra sovint com a fre de seguretat en mecanismes (transmissions d'ascensors, tensors, etc.)
Característiques del pinyó-cremallera[modifica]

El mecanisme de cremallera està constituït per una barra amb dents, considerada com un engranatge de diàmetre infinit i un engranatge de dents rectes de menor diàmetre, i serveix per a transformar un moviment giratori de l'engranatge de menor diàmetre, en un moviment lineal o al revés.
El tren cremallera, és un exemple d'ús. Aquest tipus de tren s'utilitza quan s'han de superar grans pendents.
Dos altres exemples d'ús són el carranquí o martinet, emprat per parar la ballesta amb arc d'acer, i l'ormeig homònim emprat posteriorment per aixecar peces d'artilleria. Avui en dia es fa servir també en els mecanismes de direcció dels automòbils.
Característiques dels engranatges planetaris[modifica]
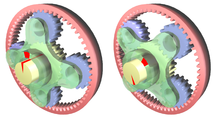
Les etapes d'engranatges planetaris, o epicicloïdals, utilitzen braços giratoris porta-satèl·lits units a l'eix que permeten el gir de rodes dentades anomenades planetes o satèl·lits que es traslladen dins d'una òrbita a l'hora que gira sobre el seu propi eix.

En la topologia més estesa i utilitzada d'etapa reductora els satèl·lits engranen alhora amb un engranatge anomenat planeta i amb un engranatge de dentat interior anomenat corona o roda interna. Aquesta nomenclatura fa referència a l'analogia amb els satèl·lits que giren entorn del planeta, en anglès es fa referència a l'analogia dels planetes que giren entorn del sol i s'anomena "sun" (sol) a la roda central "planet carrier" (porta-planetes) al porta-satel·lits i "ring" o "anulus" (anell) a la corona. Generalment la corona està fixada al càrter, el planeta rep el parell d'entrada i fa girar els satèl·lits al seu voltant aconseguint una reducció de velocitat molt elevada a l'eix de sortida solidari al porta-satèl·lits. La mateixa topologia s'empra com a multiplicador amb el portasatèl·lits com a eix d'entrada i la corona com a eix de sortida.
L'exemple més representatiu de l'ús d'aquest sistema, són els cubo-reductors de les rodes poteriors d'alguns camions, o les caixes de canvis automàtiques.
Les relacions de transmissió existents en aquestos sistemes es poden deduir segons la fórmula de Willis[18]
- = Valor algebraic de la velocitat angular de la roda conductora.
- = Valor algebraic de la velocitat angular de la darrera roda conduïda.
- = Valor algebraic de la velocitat angular del xassís.
- = Nombre de dents del planetari.
- = Nombre de dents d'un dels satèl·lits.
- = Nombre de dents de la corona anular.
- = Nombre de satèl·lits no iguals en z.
Característiques dels engranatges cònics[modifica]

Els engranatges cònics poden ser de dents rectes o helicoidals i s'utilitzen per transmetre moviments entre eixos que per les seves característiques de treball es tallen a un angle determinat.
A més, en els engranatges cònic espiral, hi existeixen tres sistemes d'espiral que són Klingelnberg, Gleason i Oerlikon, segons sigui el sistema de tallat, i en automoció s'utilitza molt l'espiral Hipoide, que és quan els eixos es creuen en diferents plans, (normalment el pinyó està desplaçat respecte al centre de la corona). S'utilitzen molt en el pont posterior de l'automòbil.
Un lloc on de segur hi trobarem engranatges cònics rectes, és en el sistema diferencial de qualsevol vehicle.

* 1 Corona cònica espiral del diferencial
* 2 Satèl·lit del diferencial
* 3 i 4 Pinyó cònic espiral (entrada força)
* 5 i 7 Semieixos o Paliers (sortida força a les rodes)
* 6 Planetaris del diferencial

* en primer terme el pinyó, amb l'eix desplaçat sota l'eix de la corona
* En el lateral la corona cònica espiral hipoide
Rendiment[modifica]
En el cas d'engranatges cilíndrics rectes el rendiment es pot estimar amb la següent fórmula:[19]
On és el coeficient de fregament, N1 i N₂ són respectivament el nombre de dents del pinyó i de la roda (o de la corona en engranatges interiors). El signe és positiu si es tracta d'engranatges exteriors i negatiu si són interiors.
Aplicacions[modifica]

Les rodes dentades constitueixen un tipus d'element fonamental a la majoria de màquines. Algunes de les aplicacions més conegudes són els rellotges de tota mena o els automòbils. En aquests darrers, la funció principal dels engranatges del sistema motor és la transmissió del moviment des de l'eix d'una font d'energia, com pot ser un motor de combustió o un motor elèctric, fins a un altre eix situat a una certa distància i que ha de realitzar un treball. Fins i tot molts aparells electrònics, amb molt poca part mecànica, necessiten rodes dentades en alguna part d'ells, com és el cas dels caixers automàtics, per exemple. Poden formar part de sistemes molt complexos però també d'altres molts senzills, com per exemple en un encenedor o en una joguina de corda.
En "donar corda" en realitat estem forçant la molla espiral a estendre's. Quan la deixem anar, aquesta tendeix a recuperar el seu estat inicial. Un dels extrems de la molla és fix, però l'altre està fixat a una roda dentada, que girarà amb l'extrem de la molla quan aquesta s'enrotlla. En una joguina de corda, per exemple un cotxe, el moviment es transmet a l'eix motriu del cotxe, en aquest cas a les rodes de darrere, que en girar farà moure les rodes del cotxe i que aquest avanci. Les rodes de davant són "boges", roden només si les de darrere ho fan o si empenyem el cotxet.
Engranatge de llanterna[modifica]

Un "engranatge de llanterna" o "pinyó de llanterna", en lloc de dents, té unes barres cilíndriques paral·leles i disposades en un cercle al voltant de l'eix de gir, com les barres d'una gàbia rodona o d'una llanterna. El conjunt es manté unit per uns discs que "tanquen la gàbia" (a cada extrem), en els que hi ha inserides les varetes que formen les dents i l'eix. Els engranatges de llanterna, al tenir menys àrea de fricció, amb molt poca precisió d'ajust funcionen millor que els de pinyons sòlids, aquests necessiten una precisió molt més gran perquè funcionin mínimament bé, apart que la brutícia pot caure a través de les barres en comptes de quedar atrapada, augmentant el desgast. Són més fàcils de fer i es poden construir amb eines molt simples, ja que les dents no estan formades per fresat, sinó per forats i barres d'inserides.[20]
L'engranatge de llanterna, de vegades fou utilitzat en els rellotges, on havia de ser mogut per una roda dentada, que no s'utilitzava com a regulador.[21][22] L'engranatge de llanterna no va ser inicialment de la devoció dels fabricants de rellotges conservadors. Es va fer popular en rellotges de torre on les condicions de treball eren més adequades. Es van utilitzar molt sovint, en els moviments dels rellotges nacionals americans.
Terminologia catalana[modifica]
- Almàstec
- Els almàstecs són les barretes cilíndriques que fan l'ofici de dents en les rodes de llanterna de sínies i molins d'aigua.[23]
Referències[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Engranatge |
- ↑ «Engranatge». Gran Diccionari de la Llengua Catalana. Barcelona: Grup Enciclopèdia Catalana.
- ↑ Derek J. de Solla Price, On the Origin of Clockwork, Perpetual Motion Devices, and the Compass, p.84
- ↑ «The Antikythera Mechanism Research Project: Why is it so important?». Arxivat de l'original el 2012-05-04. [Consulta: 10 gener 2011]. «The Mechanism is thought to date from between 150 and 100 BC»
- ↑ Norton 2004, p. 462
- ↑ Lewis, M. J. T. «Gearing in the Ancient World». Endeavour, 17, 3, 1993, pàg. 110–115. DOI: 10.1016/0160-9327(93)90099-O.
- ↑ Segment gear, TheFreeDictionary.com
- ↑ 7,0 7,1 Donald Hill (2012), The Book of Knowledge of Ingenious Mechanical Devices, page 273, Springer Science + Business Media
- ↑ 8,0 8,1 Irfan Habib, Economic History of Medieval India, 1200-1500, page 53, Pearson Education
- ↑ Joseph Needham (1986). Science and Civilization in China: Volume 4, Part 2, page 298. Taipei: Caves Books, Ltd.
- ↑ Neumaier, Robert. Hermetic Pumps:: The Latest Innovations and Industrial Applications of Sealless Pumps.. Gulf Professional Publishing, 8 juliol 1997, p. 392–. ISBN 978-0-08-053392-6.
- ↑ Huygens, Christiaan. Horologium oscillatorium: sive de motu pendulorum ad horologia aptato demonstrationes geometricae. F. Muguet, 1673.
- ↑ Watson, H.J.. Modern Gear Production. Elsevier Science, 22 octubre 2013, p. 240–. ISBN 978-1-4831-5734-4.
- ↑ Engranatge a l'USPTO (anglès)
- ↑ Patent USA 2906143.[Enllaç no actiu]
- ↑ Dobre, George. Power Transmissions: Proceedings of the 4th International Conference, held at Sinaia, Romania, June 20-23, 2012. Springer Science & Business Media, 11 juliol 2013, p. 76–. ISBN 978-94-007-6558-0.
- ↑ Engranatges cilíndrics rectes (Mecanica Teorica y Aplicada, Ediciones Tea, S.A., pag M. 88)
- ↑ Casillas, A. L.. Máquinas : cálculo de taller (en castellà). 38a. ed., edición hispanoamericana. Madrid: Ediciones Máquinas, [D.L. 2004.], p. 197. ISBN 84-400-7216-3.
- ↑ Mecanica Teórica y Aplicada, Pag. M95, Ed. Tea s.a.
- ↑ Enciclopèdia Espasa, Article "Engranatge", pàgina 1375 tomo 19
- ↑ Mariano Maymó. Guía del industrial, ó, Manual de mecánica práctica: con varias tablas y cálculos para uso de los constructores contra-maestres, mayordomos, directores de fábricas e industriales en general. Juan Roger, 1858, p. 228–.
- ↑ Ferdinand Berthoud. Histoire de la mesure du temps par les horloges. la République, 1802, p. 235–.
- ↑ D'ací i d'allà. Editorial Catalana, 1921.
- ↑ Artur Bladé i Desumvila. El castell de Miravet. Rafael Dalmau., 1966.
















