Torsió (mecànica)
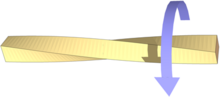

A l'entorn de l'enginyeria, torsió és la sol·licitació que es presenta quan s'aplica un moment sobre l'eix longitudinal d'un element constructiu o prisma mecànic, com poden ser eixos o, en general, elements on una dimensió predomina sobre les altres dues, encara que és possible trobar-la en situacions diverses.
La torsió es caracteritza geomètricament perquè qualsevol corba paral·lela a l'eix de la peça deixa d'estar continguda en el pla format inicialment per les dues corbes. En lloc d'això una corba paral·lela a l'eix es retorça voltant d'ell (vegeu torsió geomètrica).
L'estudi de la torsió és complicat perquè sota aquest tipus de sol·licitació la secció transversal d'una peça en general es caracteritza per dos fenòmens:
- Apareixen tensions tangencials paral·leles a la secció transversal. Si aquestes es representen per un camp vectorial seus línies de flux "circulen" al voltant de la secció.
- Quan les tensions anteriors no estan distribuïdes adequadament, cosa que passa sempre a menys que la secció tingui simetria circular, apareixen Curvatura seccionals que fan que les seccions transversals deformades no siguin planes.
El alabeig de la secció complica el càlcul de tensions i deformacions, i fa que el moment torsor pugui descompondre en una part associada a torsió bombada i una part associada a la crida torsió de Saint-Venant . En funció de la forma de la secció i la forma del alabeig, poden utilitzar-se diverses aproximacions més simples que el cas general.
Torsió general: Dominis de torsió[modifica]
En el cas general es pot demostrar que el gir relatiu d'una secció no és constant i no coincideix tampoc amb la funció de alabeig unitari. A partir del cas general, i definint l'esveltesa torsional com:
On G, E són respectivament el mòdul d'elasticitat transversal i el mòdul elasticitat longitudinal, J, I ω són el mòdul torsional i el moment de alabeig i L és la longitud de la barra recta. Podem classificar els diversos casos de torsió general dins de límits on resultin adequades les teories aproximades exposades a continuació.
D'acord amb Kollbruner i Basler:[1]
- Torsió de Saint-Venant pura , quan .
- Torsió de Saint-Venant dominant , quan .
- Torsió bombada mixta , quan .
- Torsió bombada dominant , quan .
- Torsió bombada pura , quan .
El càlcul exacte de la torsió en el cas general es pot dur a terme mitjançant mètodes variacionals o usant un lagrangià basat en l'energia de deformació. El cas de la torsió bombada mixta només pot ser tractat la teoria general de torsió. En canvi la torsió de Saint-Venant i la torsió bombada pures admesos algunes simplificacions útils.
Torsió de Saint-Venant pura[modifica]
La teoria de la torsió de Saint-Venant és aplicable a peces prismàtiques de gran inèrcia torsional amb qualsevol forma de secció, en aquesta simplificació s'assumeix que l'anomenat moment de alabeig és nul, la qual cosa no vol dir que el alabeig seccional també ho sigui. La teoria de torsió de Saint-Venant dona bones aproximacions per a valors , això sol complir-se en:
- Seccions massisses de gran inèrcia torsinal (circulars o d'una altra manera).
- Seccions tubulars tancades de paret prima.
- Seccions multicel de paret prima.
Per seccions no circulars i sense simetria de revolució la teoria de Sant-Venant a més d'un gir relatiu de la secció transversal respecte a l'eix baricentre prediu un alabeig seccional o curvatura de la secció transversal. La teoria de Coulomb de fet és un cas particular en què el alabeig és zero, i per tant només hi ha gir.
Torsió recta: Teoria de Coulomb[modifica]
La teoria de Coulomb és aplicable a eixos de transmissió de potència massissos o buits, a causa de la simetria circular de la secció no poden existir Curvatura diferencials sobre la secció. D'acord amb la teoria de Coulomb la torsió genera una tensió tallant el qual es calcula mitjançant la fórmula:
On:
- : Esforç tallant a la distància .
- : Moment torsor total que actua sobre la secció.
- : distància des del centre geomètric de la secció fins al punt on s'està calculant la tensió tallant.
- : Mòdul de torsió.
Aquesta equació es basa en la hipòtesi cinemàtica de Coulomb sobre com es deforma una peça prismàtica amb simetria de revolució, és a dir, és una teoria exclusiva elements secció circular o circular buida. Per peces amb secció d'aquest tipus es suposa que l'eix baricentre roman inalterat i qualsevol altra línia paral·lela a l'eix es transforma en una espiral que gira al voltant de l'eix baricentre, és a dir, s'admet que la deformació ve donada per uns desplaçaments del tipus:
El tensor de deformacions per a una peça torsion com l'anterior s'obté derivant adequadament les anteriors components del vector de desplaçament:
A partir d'aquestes components del tensor de deformacions utilitzant les equacions de Lame-Hooke fan que el tensor tensió ve donat per:
Usant les equacions d'equivalència s'arriba a la relació existent entre la funció α i el moment torsor:
On , és el moment d'inèrcia polar que és la suma dels segons moments d'àrea.
Torsió no recta: Teoria de Saint-Venant[modifica]
Per a una barra recta de secció no circular a més del gir relatiu apareixerà un petit alabeig que requereix una hipòtesi cinemàtica més complicada. Per representar la deformació es pot prendre un sistema d'eixos en què X coincideixi amb l'eix de la biga i llavors el vector de desplaçaments d'un punt de coordenades ( x, y, z ) ve donat en la hipòtesi cinemàtica de Saint-Venant per:
On és el gir relatiu de la secció (sent la seva derivada constant), sent z C i yC les coordenades del centre de tallant respecte al centre de gravetat de la secció transversal i sent ω ( y, z ) la funció de alabeig unitari que dona els desplaçaments perpendiculars a la secció i permeten conèixer la forma corbada final que tindrà la secció transversal. Convé assenyalar, que la teoria en postular que la derivada del gir és constant és només una aproximació útil per a peces de gran inèrcia torsional.
Calculant les components del tensor de deformacions a partir de les derivades del desplaçament s'ha de:
Calculant les tensions a partir de les anteriors deformacions i introduint-les en l'equació d'equilibri elàstic s'arriba a:
Analogia de la membrana de Prandtl[modifica]
Per seccions massisses de gran rigidesa torsional la distribució de les tensions associades a la torsió té una analogia mecànica amb la deformació d'una membrana elàstica quasiplana. Concretament Prandtl va provar el 1903 que la forma que adopta la membrana pot relacionar-se amb una funció de tensions les derivades donen les tensions tangencials en cada direcció.[2] Dit d'una altra manera el pendent d'una membrana de Prandtl deformada coincideixen amb les tensions tangencials de torsió d'un prisma mecànic la secció transversal tingui precisament la mateixa manera que la membrana.
Seccions tancades simples de paret prima[modifica]
En aquest cas les tensions tangencials poden considerar aproximadament constants sobre una línia paral·lela al gruix de la peça, és a dir, perpendicular al contorn exterior de la peça. La tensió tangencial en aquest cas pot expressar-se mitjançant:
On:
- , és l'àrea tancada per la línia mitjana de la secció tubular.
- , és el gruix de la secció tubular al punt s de la corba del contorn.
Mentre que el gir:
En cas que el gruix sigui i ( s ) = i 0 constant aquesta última equació es redueix a:
Torsió bombada pura[modifica]
Per peces de molt escassa inèrcia torsional, com les peces de paret prima obert, podeu construir-se un conjunt d'equacions molt simples en què gairebé tota la resistència a la torsió es deu a les tensions tallants induïdes pel alabeig de la secció. En la teoria de torsió bombada pura es fa servir l'aproximació que el moment d'alabeig coincideix amb el moment torsor total. Aquesta teoria s'aplica especialment a peces de paret prima oberta, on no apareixen esforços de membrana.
Seccions obertes de paret prima[modifica]
Per un rectangle molt allargat ( b << a ) la tensió tangencial màxima i el gir poden aproximar per:
Per un perfil I o perfil H que pot ser aproximat unint rectangles de dimensions (dues ales rectangualres allargades i una ànima rectangular allargada) les expressions anteriors es poden generalitzar a:
On τ i, màx és la tensió tangencial màxima sobre el rectangle i -èsim, b i és el gruix (ample) d'aquest rectangle i a i seu llarg.
Torsió mixta[modifica]
En el domini de torsió de Saint-Venant dominant i de torsió bombada dominant, poden emprar-se amb cert grau d'aproximació la teoria de Sant-Venant i la teoria de torsió bombada. No obstant això en el domini central de torsió extrema, es cometen errors importants i és necessari que useu la teoria general més complicada.
On les magnituds geomètriques són respectivament el segon moment de alabeig i el mòdul de torsió i els "esforços" es denominen bimoment i moment d'alabeig, tots ells definits per prismes mecànics.
Referències[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Torsió |
- Ortiz Berrocal, L., Elasticitat , McGraw-Hill, 1998, ISBN 84-481-2046-9.
- Timoixenko, S.P. i Godia JN, Theory of elasticity , McGraw-Hill, 1951.
- Monleón Cremades, S., Anàlisi de bigues, arcs, plaques i làmines , Ed UPV, 1999, ISBN 84-7721-769-6.





![{\displaystyle \lambda _{T}\in (1/2,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13c360bc0c097060f66c8d1bf3146771de4423ae)
![{\displaystyle \lambda _{T}\in (0,1/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aec9cc5e60731c4e95e1dc9e7ae35f8e5ea7607f)
















![{\displaystyle {\begin{matrix}\varepsilon _{xx}={\cfrac {\partial u_{x}}{\partial x}}=\omega {\cfrac {d\theta _{x}}{dx}}&&\varepsilon _{xy}={\cfrac {1}{2}}\left[{\cfrac {\partial u_{x}}{\partial y}}+{\cfrac {\partial u_{y}}{\partial x}}\right]={\cfrac {1}{2}}\left[{\cfrac {\partial \omega }{\partial y}}-(z-z_{C})\right]{\cfrac {d\theta _{x}}{dx}}\\\varepsilon _{yy}={\cfrac {\partial u_{y}}{\partial y}}=0&&\varepsilon _{xz}={\cfrac {1}{2}}\left[{\cfrac {\partial u_{x}}{\partial z}}+{\cfrac {\partial u_{z}}{\partial x}}\right]={\cfrac {1}{2}}\left[{\cfrac {\partial \omega }{\partial y}}+(y-y_{C})\right]{\cfrac {d\theta _{x}}{dx}}\\\varepsilon _{zz}={\cfrac {\partial u_{z}}{\partial z}}=0&&\varepsilon _{yz}={\cfrac {1}{2}}\left[{\cfrac {\partial u_{y}}{\partial z}}+{\cfrac {\partial u_{z}}{\partial y}}\right]=0\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf4504c04a9acf9611fe645ec855ad3d6ea71393)









![{\displaystyle \mathbf {T} _{tor}={\begin{bmatrix}\sigma _{xx}&\tau _{xy}&\tau _{xz}\\\tau _{xy}&0&0\\\tau _{xz}&0&0\end{bmatrix}}\qquad {\begin{cases}\sigma _{xx}=\omega {\cfrac {B_{\omega }}{I_{\omega }}}\\\tau _{xy}=-{\cfrac {1-\kappa _{0}}{\kappa _{0}}}\left[{\cfrac {\partial \omega }{\partial y}}+z_{C}\right]{\cfrac {M_{\omega }}{J}}+\left[{\cfrac {\partial \omega }{\partial y}}-(z-z_{C})\right]{\cfrac {M_{x}-M_{\omega }}{J}}\\\tau _{xz}=-{\cfrac {1-\kappa _{0}}{\kappa _{0}}}\left[{\cfrac {\partial \omega }{\partial y}}-y_{C}\right]{\cfrac {M_{\omega }}{J}}+\left[{\cfrac {\partial \omega }{\partial y}}+(y-y_{C})\right]{\cfrac {M_{x}-M_{\omega }}{J}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50e5283be684685f0d8d1439bf935393295f0057)

