Simetria

L'home de Vitruvi, de Leonardo da Vinci (ca. 1487), és una representació freqüent de la simetria del cos humà, i per extensió del món natural.

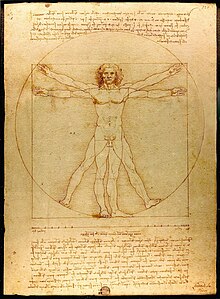
El concepte de simetria (del grec συμμετρεῖν, mesurar conjuntament) és un terme molt usat en les diferents branques de les ciències. En general, es denomina simetria al fet que certs objectes no canvien quan s'aplica una determinada operació.

Aquesta definició tan àmplia es pot visualitzar amb el següent exemple: suposem que ens col·loquem davant d'un mirall amb els peus i els braços estesos. Aviat comprovarem que la part esquerra i dreta del nostre cos son (com a mínim a primer cop d'ull) iguals. Aquest exemple és el que s'anomena simetria bilateral. En aquest cas l'objecte seria el nostre cos i l'operació és la comparació entre els dos costats.

És un concepte que en general comporta dos significats principals. El primer comporta una sensació imprecisa d'harmonia o des d'un punt de vista estètic, d'agradable proporcionalitat i equilibri, que reflecteix la bellesa o la perfecció. Per aquest motiu la simetria apareix a nombrosos símbols i artefactes culturals, ja que alguns psicòlegs defensen que l'home busca l'harmonia simètrica de manera instintiva, fins i tot es podria relacionar amb l'atracció sexual, essent els rostres més simètrics els que es qualifiquen amb més freqüència com a atractius.

El segon significat és un concepte precís i ben definit d'equilibri o "patró d'auto-similitud" que pot ser demostrat o provat d'acord amb les regles d'un sistema formal: mitjançant la geometria, a través de la física o des d'altres disciplines. Encara que, en alguns contextos, els significats es distingeixen, els dos significats de "simetria" estan relacionats i s'estudien de manera paral·lela.

La simetria és un tret característic de formes geomètriques, sistemes, equacions, i altres objectes materials o entitats abstractes, relacionada amb la seva invariància sota certes transformacions, moviments o intercanvis. En condicions formals, diem que un objecte és simètric pel que fa a una operació matemàtica donada si, quan aplicat a l'objecte, aquesta operació no canvia l'objecte o el seu aspecte. Pel que fa a un grup donat d'operacions, dos objectes són simètrics un a l'altre si un és obtingut d'un altre per algunes operacions (i viceversa). En la geometria 2D les principals classes de simetria d'interès són les que concerneixen a les isometries d'un espai euclidià: translacions, rotacions, reflexions i reflexions que llisquen.

La simetria també es troba en organismes vius.

Simetria en geometria

Vegeu també: Funció simètrica

Grup de simetria de l'esfera

Quan es parla d'objectes físics o elements geomètrics el concepte de simetria està associat a transformacions geomètriques com ara les rotacions, les reflexions o les translacions. Així es diu que un objecte presenta una:

• Simetria esfèrica, si hi ha simetria sota qualsevol rotació possible, matemàticament equival a que el grup de simetria d'un objecte físic o entitat matemàtica sigui un SO(3).
• Simetria cilíndrica o axial, si hi ha un eix tal que els girs al voltant d'ell no condueixen a canvis de posició en l'espai, matemàticament està associat a un grup d'isometria SO(2).
• Simetria reflectiva. Es defineix per l'existència d'un únic pla, que matemàticament està associat al grup SO(1) o la seva representació equivalent $\mathbb{Z}_2$.

Dues simetries senzilles són la simetria axial i la simetria central; aquest últim és la simetria esfèrica reduïda a dues dimensions.

Simetria en física

Primera zona de Brillouin d'una xarxa CCC amb etiquetes de simetria

En física el concepte de simetria està molt estretament lligat a la invariància del Hamiltonià o del Lagrangià. Bàsicament es tracta d'un conjunt d'operacions (com per exemple la translació o la rotació) que no produeixen cap canvi en el sistema, això és, el deixen invariant.

Per veure-ho es pot fer servir el següent exemple il·lustratiu. Suposant que existeix un sistema que està descrit per un Lagrangià L i que aquest és invariant sota la translació:

$q_i \to q_i + \delta q_i$

on $q_i$ denota la posició de la partícula. El fet que L "és invariant" sota la translació s'expressa matemàticament com:

$\frac{\partial L}{\partial q_i} = 0$

És a dir: el sistema no depen d'aquesta. Si s'aplica això a les equacions de Lagrange:

$\frac{d}{dt} \frac{\partial L}{\partial \dot{q_i}} - \frac{\partial L}{\partial q_i} = 0$

aleshores s'obté que:

$\frac{d}{dt} \frac{\partial L}{\partial \dot{q_i}} = \frac{dp_i}{dt} = 0$

on s'ha fet servir la definició de moment canònic:

$p_i = \frac{\partial L}{\partial \dot{q_i}}$

Per tant: si L és invariant respecte la translació a $q_i$, llavors el moment canònic conjugat (el corresponent a $q_i$) és constant (diem que es conserva, que no canvia en el temps).

El teorema central que tracta les simetries és el teorema de Noether. Grosso modo, ve a dir que per cada simetria existeix una quantitat conservada. En l'exemple que s'ha citat més amunt: a la simetria de translació li correspon la conservació del moment.

Simetria en química

En química la simetria geomètrica de les molècules és important, particularment en química orgànica. A més propietats com el seu moment dipolar i les transicions espectroscòpiques permeses (basades en regles de selecció com la regla de Laporte) poden predir o ser explicades a partir de la simetria de la molècula. Les simetries que apareixen en química estan associades a grups finits de isometries, en concret són grups puntuals de transformacions de isometria.

Simetria en biologia

Il·lustració dels diferents tipus de simetria en les formes orgàniques (Field Museum, Chicago)

Simetria en biologia és l'equilibrada distribució en el cos dels organismes d'aquelles parts que apareixen duplicades. Els plans corporals de la majoria d'organismes pluricelulares exhibeixen alguna forma de simetria, bé sigui simetria radial o simetria bilateral. Una petita minoria no presenta cap tipus de simetria (són asimètrics).

Simetria radial

La simetria radial és la simetria definida per un eix heteropolar (diferent en els seus dos extrems). L'extrem que conté la boca es diu costat oral, i el seu oposat costat aboral o abactinal. Sobre aquest eix, s'estableixen plans principals de simetria, dues perpendiculars que defineixen les posicions per-radials. Les estructures en altres plans (bisectrius dels per-radials) queden en posicions inter-radials. La zona entre els per-radials i els inter-radials és la zona ad-radial.

En el passat, els animals amb simetria radial han estat classificats com a clade propi diverses vegades amb el nom de Radiata. Aquest terme ha estat aplicat als equinoderms, tot i que en realitat pertanyen al clade Bilateria, car presenten simetria bilateral al principi del seu desenvolupament.

L'any 1983, Thomas Cavalier-Smith definí un subregne anomenat Radiata, compost pels fílums Porifera, Myxozoa, Placozoa, Cnidaria i Ctenophora (és a dir, tots els animals que no són bilateris). La classificació de cinc regnes de Lynn Margulis i K. V. Schwartz només classifica els cnidaris i els ctenòfors dins del clade Radiata.

Les classificacions cladístiques actuals no reconeixen Radiata com a clade vertader.

Simetria bilateral

La majoria d'espècies animals té simetria bilateral i pertany per tant al grup Bilateria, encara que hi ha espècies com els eriçons i les estrelles de mar que presenten simetria radial secundària (les fases de desenvolupament primerenques i les larves tenen simetria bilateral que posteriorment es perd en el adult). La simetria bilateral permet la definició d'un eix corporal en la direcció del moviment, la qual cosa afavoreix la formació d'un sistema nerviós centralitzat i la cefalització.

La simetria aporta evidències de salut i alguns estudiosos busquen la relació entre aquesta i l'atractiu físic, ja que s'ha postulat que els éssers vius, especialment els humans, cerquen de manera instintiva la simetria com a garantia d'una reproducció sense problemes i per tant es considerarien més atractives les persones amb una cara ben simètrica. Les conclusions, però, no són definitives

Simetria en música

En música clàssica, hi ha composicions en les quals podem trobar distribucions de les notes generades mitjançant simetria bilateral, translació o girs de mitja volta. Alguns exemples de composicions, són: el Preludi de Johann Sebastian Bach, la Sonata en G major de Domenico Scarlatti, Lotosblume de Robert Schumann, o Die Meiestersinger de Richard Wagner.

Simetria en moral

En la moral es pot donar simetria en dos sentits, en la reciprocitat i en l'empatia. En el primer, una persona rep o espera rebre un tracte igual al que ha donat, per tant és una simetria de la conducta, que obliga a un comportament anàleg en l'altre i que es troba formulada en l'anomenada Regla d'Or de l'ètica, base de molts manaments en diferents cultures. L'empatia, en canvi, igual que la simpatia i altres sentiments similars, es refereix a una simetria emocional, on hom és capaç de reproduir o apropar-se a la situació del proïsme i entendre'l millor.

Simetria en alimentació d'AC

En el context de l'electrònica de radiofreqüència, es parla d'una alimentació simètrica d'AC quan cap dels conductors està a la massa. Quan un dels conductors està a la massa i l'altre experimenta les variacions de tensió, es diu que l'alimentació és asimètrica.

Existeixen importants aplicacions tecnològiques basades en l'alimentació simètrica, ja que l'alimentació simètrica té el gran avantatge que la pèrdua de potència en la línia de transmissió és un ordre de magnitud menor que l'alimentació asimètrica per cable coaxial.

• En efecte, el camp altern generat pel conductor ascendent és cancel.lat pel camp generat pel seu homòleg descendent.
• A més, l'alimentació simètrica en delta permet la simplificació de la construcció.

L'alimentació simètrica és per tant l'alimentació preferida en l'operació QRP i en la manera EME, maneres on cada dB de guany compte.

Bibliografia

• Wald, Robert M. Chicago University Press. General relativity (en anglès), 1984. ISBN 0-226-87032-4 [Consulta: ¡]. 

Enllaços externs

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Simetria

• Calotta: A World of Symmetry
• Dutch: Symmetry Around a Point in the Plane
• Chapman: Aesthetics of Symmetry
• ISIS Symmetry
• International Symmetry Association – ISA
• Institute Symmetrion