Velocitat angular
 | |
| Unitats | radian per segon i segon invers |
|---|---|
| Fórmula | |
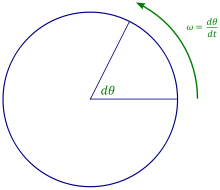
La velocitat angular, també anomenada velocitat de rotació, i de vegades pulsació o freqüència angular, està compresa en el concepte general de velocitat o variació d'una magnitud, en aquest cas la mesura d'un angle, amb el temps.[1] El seu ús més important es dona a l'estudi de moviments periòdics com el moviment circular i el moviment harmònic. La unitat de mesura per a la velocitat angular al Sistema Internacional d'unitats és el radiant per segon (rad·s−1)
La introducció del concepte és de gran importància per la simplificació que suposa en la descripció del moviment de rotació del sòlid, ja que, en un instant donat, tots els punts del sòlid posseeixen la mateixa velocitat angular, mentre que a cadascun d'ells li correspon una velocitat tangencial que és funció de la seva distància a l'eix de rotació. Així doncs, la velocitat angular caracteritza al moviment de rotació del sòlid rígid entorn d'un eix fix.
Encara que es defineix per al moviment de rotació del sòlid rígid, també s'empra en la cinemàtica de la partícula o punt material, especialment quan aquesta es mou sobre una trajectòria tancada (circular, el·líptica, etc.).[2]
Velocitat angular mitjana[modifica]
El mòdul de la velocitat angular mitjana es defineix per la relació entre l'angle d'escombrat d'un vector que gira amb centre de rotació en el punt inicial i el temps necessari per realitzar aquesta rotació. És a dir,
on ω és la velocitat angular, Δθ és l'angle recorregut i Δt és el temps emprat per recórrer l'angle.
El mòdul de la velocitat instantània angular es defineix com el límit al que tendeix la relació anterior quan l'interval de temps considerat tendeix a zero. En forma matemàtica hi ha:
Expressant la velocitat en una forma més concisa es pot escriure:
com la primera derivada de la mesura angular
En el cas del moviment circular, la velocitat angular valdria:
perquè, el temps T, que al moviment circular uniforme és el període, l'angle descrit és 2π radiants. La magnitud escalar f és la inversa de T, i en el moviment circular uniforme rep el nom de freqüència, en aquest context, ω també pot prendre el nom de pulsació.
Vector velocitat angular[modifica]

Per la velocitat angular és possible definir una direcció i un sentit, això li dona les característiques d'un vector. Com a direcció s'assumeix la de l'eix de rotació, és a dir, la normal o perpendicular al pla de rotació, mentre que el sentit vindrà donat per la regla de la mà dreta.
Sobre aquesta base, el vector de velocitat d'un punt descrivint una trajectòria circular de radi r amb velocitat angular ω forma de mòdul ω seria:
Referències[modifica]
- ↑ «angular.xml Velocitat angular». Gran Enciclopèdia Catalana. Barcelona: Grup Enciclopèdia Catalana.
- ↑ Hibbeler, R. C.. Engineering Mechanics: Dynamics (en anglès). Prentice Hall, 2009, p. 732.
Vegeu també[modifica]
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Velocitat angular |
- Rotacions i velocitat angular Arxivat 2016-03-03 a Wayback Machine. Projecte La baldufa de la Universitat Politècnica de Catalunya.








