Espai vectorial

Un espai vectorial és, en matemàtiques, i més concretament en àlgebra lineal, una estructura algebraica formada per un conjunt de vectors. Els vectors són objectes que es poden sumar entre ells i es poden multiplicar per un nombre, que en aquest context s'anomena escalar, i "aplicar-los un factor d'escala". Sovint es considera que els escalars són nombres reals, però també es poden definir espais vectorials amb la multiplicació escalar per nombres complexos, nombres racionals o, fins i tot, cossos més generals en lloc de fer servir cossos de nombres. Les operacions d'addició vectorial i multiplicació escalar han de satisfer certs requisits, anomenats axiomes, que es descriuen a la secció d'aquest article on es dona la definició formal d'espai vectorial.
Un exemple d'espai vectorial és el dels vectors euclidians, que es fan servir sovint per representar quantitats físiques com ara forces. Dues forces qualssevol (que tinguin el mateix punt d'aplicació) es poden sumar, substituint-les per una tercera força que produeixi el mateix efecte que si s'apliquen les dues alhora, i la multiplicació d'un vector força per un factor real és un altre vector força que té el mateix punt d'aplicació, direcció i sentit però el mòdul del qual s'ha multiplicat pel factor real. Un altre exemple més purament geomètric són els vectors que representen desplaçaments al pla o en l'espai tridimensional, que també formen un espai vectorial.
Els espais vectorials són l'objecte d'estudi de l'àlgebra lineal i, des d'aquest punt de vista, se'n té una comprensió profunda atès que els espais vectorials es caracteritzen per la seva dimensió que, a grans trets, especifica el nombre de direccions independents a l'espai. La teoria s'amplia introduint en els espais vectorials alguna estructura addicional, com ara una norma o un producte escalar. Aquesta mena d'espais sorgeixen de manera natural en l'anàlisi matemàtica, principalment en la forma d'espais de funcions de dimensió infinita, els vectors dels quals són funcions. Hi ha problemes analítics que requereixen l'habilitat de decidir si una successió de vectors convergeix en un vector donat. Això s'aconsegueix fent servir espais vectorials amb estructures addicionals, principalment espais dotats d'una topologia adequada, que d'aquesta manera permeten definir conceptes de proximitat i continuïtat. Aquests espais vectorials topològics, en particular els espais de Banach i els espais de Hilbert, tenen una teoria més extensa.
Històricament, les primeres idees que condueixen al concepte d'espai vectorial es poden remuntar fins al segle xvii amb els desenvolupaments de la geometria analítica, les matrius, els sistemes d'equacions lineals, i els vectors euclidians. El tractament modern, més abstracte, va ser formulat inicialment per Giuseppe Peano a finals del segle xix; inclou objectes més generals que l'espai euclidià, però gran part de la teoria es pot veure com una ampliació de les idees geomètriques clàssiques com ara línies rectes, plans i els seus anàlegs de dimensió superior.
Actualment, els espais vectorials s'apliquen a les matemàtiques, la ciència i l'enginyeria. Són la noció algebraica adequada per tractar sistemes d'equacions lineals, ofereixen una estructura per a les sèries de Fourier, que es fan servir en tècniques de compressió d'imatge, o proporciona un entorn que es pot fer servir per tècniques de solució d'equacions diferencials en derivades parcials. A més, els espais vectorials subministren una forma abstracta, independent del sistema de coordenades, per tractar amb objectes geomètrics i físics com tensors, els quals permeten examinar les propietats locals de les varietats per tècniques de linealització. Els espais vectorials també es poden generalitzar de diverses maneres, i això porta a nocions avançades de geometria i àlgebra abstracta.
Definició formal[modifica]
Sigui K un cos (per exemple, el cos dels nombres reals o el cos dels nombres complexos).
Un espai vectorial sobre el cos K és una terna =(E, +, ⋅), on E és un conjunt, + és la suma vectorial (donats elements u, v de E, la seva suma u+v és de E), i ⋅ és el producte per un escalar (donats un escalar a de K i un vector v de E, el seu producte a⋅v és de E) que satisfà les següents propietats:
- E amb la suma vectorial forma un grup abelià, és a dir, (E,+) satisfà:
- (propietat associativa);
- (el vector nul) tal que (és a dir, 0 és l'element neutre de la suma vectorial);
- tal que (és a dir, tot element té un oposat respecte a la suma);
- (propietat commutativa).
- El producte per un escalar satisfà que:
- ;
- Si 1 denota l'element neutre del producte en el cos K, llavors ;
- , propietat distributiva del producte per un escalar amb la suma vectorial.
- .
Els elements de E s'anomenen vectors. En textos impresos de vegades es ressalten en negreta (v), tal com s'ha fet en aquest article, amb una fletxa a sobre () o subratllats (v). Els elements de K s'anomenen escalars. Encara que l'espai vectorial sobre K pròpiament dit sigui la terna (E,+,⋅) és molt habitual simplificar la nomenclatura dient directament que E és un espai vectorial sobre K o també un K-espai vectorial.
Aquests axiomes permeten treballar amb la resta de vectors i la divisió d'un vector per un escalar, entenent que:
- v − w := v + (−w),
- v / a := (1 / a) · v.
Contràriament a la intuïció que prové de vectors en el cas de l'espai euclidià pla i de dimensions superiors, en espais vectorials generals no hi ha cap noció de proximitat, angles o distàncies. Per tractar aquestes qüestions, cal introduir tipus particulars d'espais vectorials amb estructures addicionals.
Història[modifica]
Els espais vectorials provenen de la geometria afí, mitjançant la introducció de sistemes de coordenades en l'espai pla o tridimensional. Al voltant de 1636, Descartes i Fermat fundaren la geometria analítica identificant les solucions d'una equació de dues variables amb punts en una corba plana.[1] El 1804, per aconseguir solucions geomètriques sense fer servir coordenades, Bolzano va introduir certes operacions sobre els punts, les línies i els plans que són predecessors de vectors.[2] Aquest treball el van realitzar l'any 1827 fent ús de la concepció de coordenades baricèntriques de Möbius.[3] L'inici de la definició de vectors va ser la noció de Bellavitis del bipunt: un segment orientat, en el qual un dels extrems és l'origen i l'altre el destí. Els vectors es van tornar a considerar amb la presentació dels nombres complexos feta per Argand i Hamilton i la concepció dels quaternions per part d'aquest darrer.[4] Són elements en ℝ² i ℝ4; el fet de tractar-los fent servir combinacions lineals és degut a Laguerre que, el 1867, també va definir els sistemes d'equacions lineals.
El 1857, Cayley presentà la notació matricial que permet una harmonització i simplificació de les aplicacions lineals. A la mateixa època, Grassmann va estudiar el càlcul baricèntric iniciat per Möbius; imaginava conjunts d'objectes abstractes dotats d'operacions.[5] En el seu treball, els conceptes d'independència lineal, dimensió i el de producte escalar ja hi són presents. De fet, el treball de Grassmann de 1844 excedeix l'estructura d'espais vectorials; a partir de la seva multiplicació albira el que actualment s'anomenen àlgebres. Peano, el 1888, va ser el primer a donar la definició moderna d'espais vectorials i aplicacions lineals.[6]
Un desenvolupament important dels espais vectorials és degut a la construcció dels espais funcionals per part de Lebesgue. Aquest desenvolupament va ser formalitzat més tard, al voltant del 1920, per Banach i Hilbert.[7] En aquella època, els especialistes comencen a interaccionar l'àlgebra i el camp nou de l'anàlisi funcional, amb conceptes clau com el d'espais de funcions p-integrables i el d'espais de Hilbert;[8] també cal incloure el de dimensió infinita, que es consolida en una noció fermament establerta, i moltes branques matemàtiques comencen a fer ús d'aquest concepte.
Exemples[modifica]
Espais de coordenades i espais funcionals[modifica]
El primer exemple d'un espai vectorial sobre un cos F és el mateix cos, proveït amb les seves addició i multiplicació estàndards. Aquest és el cas en què n = 1, en un espai vectorial que normalment es representa com Fn, i es coneix com l'espai de coordenades. Els seus elements són n-tuples (successions de longitud n):
- (a1, a₂, ..., an), on ai són elements de F.[9]
En el cas F = ℝ i n = 2, els vectors són parelles de nombres reals x i y, que es representen (x, y); l'ordre dels components es conserva de tal forma que una parella també s'anomena una parella ordenada. Aquestes parelles formen vectors tot definint, component a component, l'addició de vectors i el producte per un escalar; és a dir:
- (x1, y1) + (x₂, y₂) = (x1 + x₂, y1 + y₂)
i
- r · (x, y) = (rx, ry).
Les successions infinites de coordenades i, de forma més general, les funcions des de qualsevol conjunt donat Ω en un cos F també formen espais vectorials, definint l'addició i la multiplicació escalar punt a punt. És a dir, la suma de dues funcions ƒ i g ve donada per:
- (ƒ + g)(w) = ƒ(w) + g(w)
i el mateix succeeix amb la multiplicació. Aquests espais funcionals es donen en moltes situacions geomètriques, quan Ω és la recta real, un interval o altres subconjunts de ℝn. Moltes nocions en topologia i anàlisi, com la continuïtat, la integrabilitat o la derivabilitat respecten la linealitat: les sumes i els productes per un escalar de funcions que posseeixen tal propietat continuen tenint la mateixa propietat.[10] Per tant, els conjunts formats per aquestes funcions són espais vectorials. S'estudien amb més detall fent servir els mètodes d'anàlisi funcional.[11] Moltes construccions algebraiques també produeixen espais vectorials, un dels exemples més importants n'és l'espai vectorial F[x] dels polinomis,
- ƒ(x) = r0 + r1x + ... + rn−1xn−1 + rnxn, on els coeficients r0, ..., rn pertanyen a F.[12]
Equacions lineals[modifica]
Els sistemes d'equacions lineals homogènies estan estretament relacionats amb els espais vectorials.[13] Per exemple, les solucions de
venen donades per ternes amb a arbitrari, b = a/2, i c = −5 a/2. Formen un espai vectorial: les sumes i els productes escalars d'aquestes ternes continuen satisfent les mateixes proporcions entre les tres variables; per tant també són solucions. Les matrius es poden fer servir per condensar múltiples equacions lineals com les d'abans en una equació vectorial, és a dir
- Ax = 0,
on A = és la matriu que conté els coeficients de les equacions donades, x és el vector (a, b, c), Ax denota la multiplicació de matrius i 0 = (0, 0) és el vector zero. De manera similar, les solucions d'equacions diferencials lineals homogènies formen espais vectorials. Per exemple
- ƒ''(x) + 2ƒ'(x) + ƒ(x) = 0
dona ƒ(x) = a e−x + bx e−x, on a i b són constants arbitràries, i ex és la funció exponencial.
Extensions de cossos[modifica]
Les extensions de cossos F / E ("F sobre E") subministren una altra classe d'exemples d'espais vectorials, de forma particular en àlgebra i en teoria algebraica de nombres: un cos F que conté un cos més petit E esdevé un E-espai vectorial amb les operacions de multiplicació i addició de F.[14] Per exemple el cos ℂ dels nombres complexos és un ℝ-espai vectorial. Un tipus d'extensió de cossos que té un interès particular en teoria de nombres és ℚ(α), l'extensió dels nombres racionals ℚ per un nombre complex fixat α. ℚ(α) és el cos més petit que conté els racionals i el nombre complex fixat α. La seva dimensió com a espai vectorial sobre ℚ depèn de l'elecció de α.
Bases i dimensió[modifica]

Les bases mostren l'estructura dels espais vectorials d'una manera concisa. Una base es defineix com un conjunt (finit o infinit) B = {vi}i ∈ I de vectors vi indexats per algun conjunt índex que per combinació lineal genera tot l'espai, i és mínim amb aquesta propietat. En el cas d'un espai vectorial de dimensió finita, l'anterior afirmació vol dir que qualsevol vector v es pot expressar com una suma finita (anomenada combinació lineal dels elements base)
- v = a1v1 + a₂v₂ + ... + anvn,
on els ak són escalars i vk (k = 1, ..., n) són elements de la base B. Per altra banda, el fet de ser mínima es formalitza exigint que els elements de B siguin linealment independents. Es diu que un conjunt de vectors és linealment independent si cap dels seus elements es pot expressar com a combinació lineal dels altres. Això és equivalent a dir que l'equació
- a1v1 + a₂v₂ + ... + anvn = 0
es pot complir si i només si tots els escalars a1, ..., an són igual a zero. La independència lineal garanteix que la representació de qualsevol vector com a combinació lineal dels vectors de la base (l'existència de la qual es garanteix per l'exigència que la base generi V) és única.[15]
Això es coneix com el punt de vista coordinaditzat dels espais vectorials, pel fet de veure els vectors de la base com una generalització dels vectors de coordenades x, y, z de ℝ3 i de forma similar en cas de dimensions superiors.
Els vectors de coordenades e1 = (1, 0, ..., 0), e₂ = (0, 1, 0, ..., 0), fins a en = (0, 0, ..., 0, 1), formen una base de Fn, anomenada la base canònica, atès que qualsevol vector (x1, x₂, ..., xn) es pot expressar de forma única com una combinació lineal d'aquests vectors:
- (x1, x₂, ..., xn) = x1(1, 0, ..., 0) + x₂(0, 1, 0, ..., 0) + ... + xn(0, ..., 0, 1) = x1e1 + x₂e₂ + ... + xnen.
Tot espai vectorial té una base. Això resulta del Lema de Zorn, una formulació equivalent de l'axioma d'elecció.[16] Donats els altres axiomes de la teoria de conjunts de Zermelo-Fraenkel, l'existència de bases és equivalent a l'axioma d'elecció.[17] El lema de l'ultrafiltre, que és més feble que l'axioma d'elecció, implica que totes les bases d'un espai vectorial donat tinguin el mateix cardinal, el mateix nombre d'elements.[18] A aquest valor se l'anomena dimensió de l'espai vectorial, i se'l denota per dim E. Si l'espai es genera per una quantitat finita de vectors (si l'espai és de dimensió finita), les afirmacions anteriors es poden demostrar sense necessitat d'aquestes aportacions fonamentals procedents de la teoria de conjunts.[19]
La dimensió de l'espai de coordenades Fn és n, per la base presentada més amunt. La dimensió de l'anell de polinomis F[x] presentat més amunt és infinit numerable, una base ve donada per 1, x, x², ..., la dimensió d'espais funcionals més generals, com l'espai de funcions en alguns intervals (limitats o il·limitats), és infinita.[nb 1] Sota suposicions de regularitat adequades sobre els coeficients implicats, la dimensió de l'espai de solucions d'una equació diferencial ordinària homogènia és igual al grau de l'equació.[20] Per exemple, l'espai de solucions de l'equació de més amunt està generat per e−x i xe−x. Aquestes dues funcions són linealment independents sobre ℝ, per tant la dimensió d'aquest espai és dos, igual que el grau de l'equació.
La dimensió (o grau) del cos d'extensió ℚ(α) sobre ℚ depèn d'α. Si α satisfà alguna equació polinòmica
- qnαn + qn−1αn−1 + ... + q0 = 0, amb coeficients racionals qn, ..., q0.
("α és un nombre algebraic"), la dimensió és finita. Més precisament, és igual al grau del polinomi mínim que té α com arrel.[21] Per exemple, els nombres complexos ℂ són un espai vectorial real bidimensional, generat per 1 i la unitat imaginària i. Aquest nombre complex satisfà i² + 1 = 0, una equació polinòmica de grau dos. Per tant, ℂ és un espai vectorial real bidimensional (i, com qualsevol cos, monodimensional com a espai vectorial sobre si mateix, ℂ). Si α no és algebraic, la dimensió de ℚ(α) sobre ℚ és infinita. Per exemple, per α = π no hi ha cap equació d'aquest tipus, en altres paraules π és un nombre transcendent.[22]
Aplicacions lineals i matrius[modifica]
La relació entre dos espais vectorials es pot expressar per una aplicació lineal o transformació lineal. Són funcions que respecten l'estructura d'espai vectorial és a dir, conserven les sumes i les multiplicacions per un escalar:
- ƒ(x + y) = ƒ(x) + ƒ(y) per tot x,y del K-espai vectorial E.
- ƒ(a · x) = a · ƒ(x) per tot x, y de E, per tot a de K.[23]
Les aplicacions lineals són els morfismes dels espais vectorials. Un isomorfisme és un morfisme (aplicació lineal) bijectiu (injectiu i exhaustiu alhora). En altres paraules, és una aplicació lineal ƒ : E → F que admet una aplicació lineal inversa g : F → E, és a dir, una tal que les dues composicions possibles: ƒ ∘ g : F → F i g ∘ ƒ : E → E són la funció identitat.[24] Si existeix un isomorfisme entre E i F, es diu que els dos espais són isomorfs; llavors són essencialment idèntics com a espais vectorials, ja que totes les identitats que es compleixen a E mitjançant ƒ, es transporten a identitats similars a F, i viceversa mitjançant g.
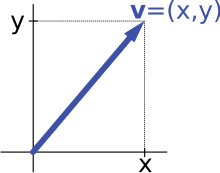
Per exemple, l'espai vectorial V₂ format pels vectors del pla i el producte cartesià dels parells de nombres reals són isomorfs: un vector al pla v que s'inicia a l'origen d'algun sistema de coordenades (fixat) es pot expressar com un parell ordenat de nombres reals prenent els components x i y de la fletxa, com es mostra en la imatge de la dreta. I viceversa, donat un parell (x, y), que va fins a x unitats cap a la dreta (o cap a l'esquerra si x és negativa), i y unitats cap amunt (cap avall si y és negativa) defineixen un vector v.
El conjunt de totes les aplicacions lineals f: E → F entre dos K-espais vectorials E i F forma un nou espai vectorial anomenat HomK(E, F), que també es denota .[25] L'espai de les aplicacions lineals de E a K s'anomena l'espai vectorial dual, i es denota E∗.[26] Mitjançant l'aplicació injectiva natural E → E∗∗, qualsevol espai vectorial es pot identificar a un subespai del seu bidual; l'aplicació és un isomorfisme si i només si l'espai és de dimensió finita.[27]
Un cop s'ha triat una base de E, les aplicacions lineals ƒ : E → F queden completament determinades especificant les imatges dels vectors base, perquè qualsevol element de E es pot expressar de forma única com una combinació lineal dels vectors de la base.[28] Si dim E = dim F, una correspondència bijectiva entre bases donades de E i F dona lloc a una aplicació lineal que a cada element de la base de E li fa correspondre un element de la base de F. És un isomorfisme, per la mateixa definició.[29] Per tant, dos espais vectorials són isomorfs si les seves dimensions concorden i viceversa. Una altra forma d'expressar això és dient que els espais vectorials estan completament ordenats (tret d'isomorfismes) per la seva dimensió. En particular, qualsevol espai vectorial E sobre K de dimensió n és isomorf a Kn. Però no hi ha cap isomorfisme "canònic" o preferit; de fet, triar un isomorfisme φ: Kn → E és equivalent a triar una base de E, fent correspondre la base canònica de Kn a E, via φ. La llibertat per triar una base adequada és de particular utilitat en el context de dimensió infinita, vegeu més avall.
Matrius[modifica]

Les matrius són una noció útil per codificar les aplicacions lineals.[30] S'escriuen com una taula rectangular d'escalars com per exemple a la imatge de la dreta. Qualsevol matriu de m-per-n es correspon a una aplicació lineal de Kn en Km, de la següent manera
- , on vol dir sumatori,
o, fent servir el producte matricial de la matriu A pel vector de coordenades x:
- x ↦ Ax.
A més fent aquesta assignació, una vegada triades les bases de E i F, qualsevol aplicació lineal ƒ : E → F té una representació matricial única.[31]

El determinant det (A) d'una matriu quadrada A és un escalar que indica si l'aplicació associada és un isomorfisme o no: perquè ho sigui és suficient i necessari que el determinant corresponent sigui diferent de zero.[32] La transformació lineal de ℝn que correspon a una matriu de n-per-n real preserva l'orientació si i només si el determinant és positiu.
Vectors propis i valors propis[modifica]
Les aplicacions lineals ƒ : E → E, anomenades endomorfismes, són especialment importants, ja que en aquest cas els vectors v es poden comparar amb la seva imatge per ƒ, ƒ(v). Qualsevol vector diferent de zero v que satisfà λv = ƒ(v), on λ és un escalar, s'anomena un vector propi de ƒ amb el valor propi λ.[nb 2][33] De forma equivalent, v és un element del nucli de la diferència ƒ − λ · Id (on Id és l'aplicació identitat E → E).). Si E té dimensió finita, això es pot reformular fent servir determinants: ƒ té valor propi λ és equivalent a
- det (ƒ − λ · Id) = 0.
Explicitant el càlcul del determinant, l'expressió de l'esquerra es pot veure com una funció polinòmica de λ, anomenada el polinomi característic de ƒ.[34] Si el cos K és prou gran per contenir un zero d'aquest polinomi (cosa que passa automàticament si K és algebraicament tancat, com en el cas K = ℂ)) qualsevol aplicació lineal té com a mínim un vector propi. L'espai vectorial E pot tenir o no una base pròpia, una base formada per vectors propis. Aquest fenomen està governat per la forma canònica de Jordan de l'aplicació.[nb 3] El conjunt de tots els vectors propis que corresponen a un valor propi particular de ƒ formen un espai vectorial conegut com l'espai propi que correspon al valor propi (i ƒ) en qüestió. Per demostrar el teorema espectral, (l'afirmació corresponent en el cas de dimensió infinita), es necessita la maquinària de l'anàlisi funcional, vegeu més avall.
Conceptes basats en espais vectorials[modifica]
A més a més dels conceptes explicats abans, hi ha uns altres conceptes algebraics que es construeixen basats en els espais vectorials i que generen espais vectorials relacionats amb un espai vectorial donat. A més a més de les definicions que es presenten a sota, també es caracteritzen per propietats universals, les quals determinen un objecte X especificant les aplicacions lineals des de X fins a qualsevol altre espai vectorial.
Subespais i espais quocient[modifica]

Un subconjunt no buit F d'un espai vectorial E tancat respecte de l'addició de vectors i la multiplicació escalar s'anomena un subespai vectorial de E.[35] Els subespais vectorials de E són espais vectorials (sobre el mateix cos). La intersecció de tots els subespais que contenen un conjunt donat S de vectors s'anomena el subespai generat (o engendrat) pels vectors de S denotat <S>, i és el subespai més petit de E que conté el conjunt S. Expressat en funció dels elements, <S> és el subespai que consisteix en combinacions lineals dels elements de S.[36]
La contrapartida als subespais generats són els espais vectorials quocient.[37] Donat qualsevol subespai N de E, l'espai quocient, E/N ("E mòdul N") es defineix de la manera següent: com a conjunt, consta de v + N = {v + w, w ∈ N}, on v és un vector qualsevol de E. La suma de dos elements d'aquest conjunt, v1 + N i v₂ + N és (v1 + v₂) + N, i la multiplicació escalar ve donada per a · (v + N) = (a · v) + N. El punt clau en aquesta definició és que v1 + N = v₂ + N si i només si la diferència entre v1 i v₂ pertany a N.[nb 4] D'aquesta manera, l'espai quocient "oblida" la informació que es conté en el subespai N.
El nucli Ker(ƒ) d'una aplicació lineal ƒ: E → F consta dels vectors v tals que tenen per imatge el 0 de F.[38] Tant el nucli com la imatge im(ƒ) = {ƒ(v), v ∈ E} són subespais de E i F respectivament.[39]
L'existència del nucli i la imatge són part del fet que la categoria dels espais vectorials (sobre un cos determinat K) és una categoria abeliana, és a dir, un corpus d'objectes matemàtics i morfismes entre ells (una categoria) que es comporta en gran manera com la categoria dels grups abelians.[40] A causa d'això, moltes afirmacions com el primer teorema d'isomorfia (també anomenat teorema del rang en termes de matrius)
- E / ker(ƒ) ≅ im(ƒ).
i el segon i tercer teorema d'isomorfia es poden formular i demostrar de forma molt similar a les afirmacions corresponents per a grups.
Un exemple important és el nucli d'una aplicació lineal x ↦ Ax per a una matriu donada A, com la de dalt. El nucli d'aquesta aplicació és el subespai format pels vectors x tals que Ax = 0, que és precisament el conjunt de les solucions del sistema d'equacions lineals homogènies que corresponen a A. Aquest concepte també s'estén a les equacions diferencials lineals
- , on els coeficients ai també són funcions de x.
En l'aplicació corresponent
- ,
les derivades de la funció ƒ hi surten de forma lineal (en oposició a ƒ''(x)², per exemple). Atès que la derivació és un procediment lineal (és a dir, (ƒ + g)' = ƒ' + g ' i (c·ƒ)' = c·ƒ' per una constant c) aquesta assignació és lineal, anomenada operador diferencial lineal. En particular, les solucions a l'equació diferencial D(ƒ) = 0 formen un espai vectorial (sobre ℝ o).
Producte directe i suma directa[modifica]
El producte directe d'una família d'espais vectorials Vi consta del conjunt de tots els tuples (vi)i ∈ I, que especifiquen, per a cada índex i d'algun conjunt índex I, un element vi de Vi.[41] L'addició i la multiplicació escalar en l'espai resultat del producte directe es fan component a component. Una variant d'aquesta construcció és la suma directa (també anomenat coproducte i notat ), on només es permeten tuples amb una quantitat finita de vectors diferents de zero. Si el conjunt índex I és finit, les dues construccions coincideixen, però si no, són diferents.
Producte tensorial[modifica]
El producte tensorial V ⊗F W, o simplement V ⊗ W, de dos espais vectorials V i W és una de les nocions centrals en àlgebra multilineal que tracta l'extensió de nocions com les aplicacions lineals a diverses variables. Una aplicació g de mapa: g: V × W → X s'anomena bilineal si g és lineal en les dues variables v i w. És a dir, per a un w fixat l'aplicació v ↦ g(v, w) és lineal en el sentit definit més amunt i el mateix passa per a un v fixat.
El producte tensorial és un espai vectorial particular que és un receptor universal d'aplicacions bilineals g, de la manera següent. Es defineix com l'espai vectorial que consta de sumes finites (formals) de símbols anomenats tensors
- v1 ⊗ w1 + v₂ ⊗ w₂ + ... + vn ⊗ wn,
subjectes a les següents regles
- a · (v ⊗ w) = (a · v) ⊗ w = v ⊗ (a · w), on a és un escalar,
- (v1 + v₂) ⊗ w = v1 ⊗ w + v₂ ⊗ w, i
- v ⊗ (w1 + w₂) = v ⊗ w1 + v ⊗ w₂.[42]

Aquestes regles asseguren que l'aplicació ƒde V × W en V ⊗ W que fa correspondre una tupla (v, w) a v ⊗ w és bilineal. La universalitat estableix que donat qualsevol espai vectorial X i qualsevol aplicació bilineal g: V × W → X,, existeix una aplicació única u, que es mostra en el diagrama amb una fletxa de punts, que composta amb ƒ dona g: u(v ⊗ w) = g(v, w).[43] Això s'anomena la propietat universal del producte tensorial, un exemple del mètode que es fa servir molt sovint en àlgebra abstracta avançada per definir objectes de manera indirecta especificant aplicacions des de o cap a l'objecte.
Espais vectorials amb estructura addicional[modifica]
Des del punt de vista de l'àlgebra lineal, els espais vectorials s'entenen completament en la mesura que qualsevol espai vectorial es caracteritza, fins a l'isomorfisme, per la seva dimensió. Tanmateix, els espais vectorials ad hoc no ofereixen una estructura per tractar amb la qüestió (fonamental per a l'anàlisi matemàtica) de si una successió de funcions convergeix cap a una altra funció. De la mateixa manera, l'àlgebra lineal no és adequada per tractar amb sèries infinites, ja que l'operació d'addició només admet l'addició d'una quantitat finita de termes. Per tant, les necessitats de l'anàlisi funcional exigeixen considerar estructures addicionals. En gran part, de la mateixa manera que el tractament axiomàtic dels espais vectorials mostra els seus trets algebraics essencials, estudiar espais vectorials amb estructures addicionals de manera abstracta també resulta ser avantatjós.
Un primer exemple d'una estructura addicional és una relació d'ordre ≤, un mètode pel qual els vectors es poden comparar.[44] Per Exemple, l'espai n-dimensional Rn es pot ordenar comparant els seus vectors component a component. Els espais vectorials ordenats, per exemple els espais de Riesz, són fonamentals per la integral de Lebesgue, que depèn de l'habilitat per expressar una funció com a diferència de dues funcions positives
- ƒ = ƒ+ − ƒ−,
on ƒ+ indica la part positiva de ƒ i ƒ− la part negativa.[45]
Espais vectorials normats i producte escalar[modifica]
"Mesurar" vectors es fa especificant una norma, una dada que mesura longituds de vectors, o també es pot fer amb un producte escalar, que mesura angles entre vectors. Les normes i els productes escalars es noten i , respectivament. El fet de donar un producte escalar implica que les llargades dels vectors també es poden definir, definint la norma associada . Els espais vectorials dotats d'aquestes estructures es coneixen com espais vectorials normats i espais amb producte escalar, respectivament.[46]
A l'espai de coordenades Fn se'l pot dotar del producte escalar estàndard:
En R², això porta a la noció habitual d'angle entre dos vectors x i y:
Degut a això, dos vectors que satisfan s'anomenen ortogonals. En l'espai de Minkowsky es fa servir una variant important del producte escalar estàndard: R4 dotat amb el producte de Lorenz
A diferència del producte escalar estàndard aquest no és una forma bilineal definida positiva: també pot tenir valors negatius, per exemple per x = (0, 0, 0, 1). Triant la quarta coordenada de forma que es correspongui amb el temps, serveix per al tractament matemàtic de la relativitat especial.
Espais vectorials topològics[modifica]
Les qüestions referents a la convergència es tracten considerant que els espais vectorials V tenen una topologia compatible, una estructura que permet parlar d'elements que són més o menys a prop els uns dels altres.[48][49] Aquí compatible vol dir que l'addició i el producte escalar han de ser funcions contínues. De forma col·loquial, si x i y de V, i a de F varien en una quantitat limitada, llavors la variació de x + y i la de a x també són limitades.[nb 5] Perquè tingui sentit especificar la quantitat de canvi d'un escalar, el camp F també ha de tenir una topologia en aquest context; una elecció habitual per al cos F és emprar el cos dels nombres reals o el dels complexos.
En aquests espais vectorials topològics es poden estudiar sèries de vectors. És a dir, les sumes infinites
denota el límit de les sumes parcials finites corresponents de la successió (ƒi)i∈N d'elements de V. Per exemple, els ƒi podrien ser funcions (reals o complexes) que pertanyen a algun espai funcional V, en aquest cas la sèrie és una sèrie de funcions. El tipus de convergència de la sèrie depèn de la topologia imposada a l'espai de funcions. En aquests casos, la convergència punt a punt i la convergència uniforme són dos exemples típics.

Una manera d'assegurar l'existència de límits de certes sèries infinites és restringir l'atenció a espais on qualsevol successió de Cauchy té límit; aquests espais vectorials s'anomenen complets. Col·loquialment, la condició que un espai vectorial sigui complet imposa la condició que contingui tots els límits necessaris. Per exemple, l'espai vectorial de polinomis en l'interval unitari [0,1], dotat amb la topologia de convergència uniforme no és complet perquè, segons el teorema de Stone-Weierstrass, tota funció contínua a [0,1] pot ser uniformement aproximada per una successió de polinomis (i no totes les funcions contínues són polinomis, per tant el conjunt dels polinomis no conté els seus límits).[50] En canvi, l'espai de totes les funcions contínues en [0,1] amb la mateixa topologia és complet.[51] Una norma dona lloc a una topologia definint que una successió de vectors vn convergeix a v si i només si
- .
Els espais de Banach i de Hilbert són espais topològics complets les topologies dels quals venen donades, respectivament, per una norma i un producte escalar. El seu estudi (peça clau en l'anàlisi funcional) se centra en l'anàlisi en espais vectorials de dimensió infinita, ja que totes les normes en espais vectorials topològics de dimensió finita donen lloc a la mateixa noció de convergència.[52] La imatge de la dreta mostra l'equivalència de la 1-norma i la ∞-norma en R²: com que les "boles" unitàries s'encaixen l'una dins l'altra, una successió convergeix a zero en una norma si i només si també ho fa en l'altra norma. Tanmateix, en el cas de dimensió infinita, en general, hi haurà topologies que no seran equivalents, això fa l'estudi d'espais vectorials topològics més rics que el dels espais vectorials sense estructures addicionals.
Des d'un punt de vista conceptual, totes les nocions relacionades amb espais vectorials topològics haurien de lligar amb la topologia. Per exemple, en comptes de considerar totes les aplicacions lineals (també anomenades funcionals) V → W, s'exigeix que les aplicacions entre espais vectorials topològics siguin contínues.[53] En particular, l'espai dual (topològic) V∗ consta de funcionals continus V → R (o C). El teorema de Hahn-Banach s'ocupa de la separació de subespais d'espais vectorials topològics apropiats per funcionals continus.[54]
Espais de Banach[modifica]
Un espai de Banach, (espais introduïts per Stefan Banach), és un espai vectorial normat complet (és a dir, tal que tota successió de Cauchy respecte a la mètrica d(x,y)=||x-y|| és convergent).[55] A és l'espai vectorial ℓ p format per vectors amb infinits components reals x = (x1, x₂, ...) la p-norma dels quals (1 ≤ p ≤ ∞) ve donada per
- for p < ∞ i
és finita. Les topologies de l'espai de dimensió infinita ℓ p no són equivalents en variar p. Per exemple la successió de vectors xn = (2−n, 2−n, ..., 2−n, 0, 0, ...), és a dir, els primers 2n components són 2−n, i els següents són 0, convergeix al vector nul per a p = ∞, però no per a p = 1:
- , però .
De forma més general que les successions de nombres reals, les funcions ƒ: Ω → R estan dotades d'una norma que substitueix la suma esmentada per la integral de Lebesgue
- .
L'espai de funcions integrables sobre un domini donat Ω (per exemple un interval) que satisfà |ƒ|p < ∞ i equipat amb aquesta norma s'anomenen espais de Lebesgue, i es noten Lp(Ω).[nb 6] Aquests espais són complets.[56] (en canvi si es fa servir la integral de Riemann, l'espai no és complet, la qual cosa es pot veure com una justificació per la teoria de la integració de Lebesgue.[nb 7]) En concret això significa que per a qualsevol successió de funcions Lebesgue integrables ƒ1, ƒ₂, ... amb |ƒn|p < ∞, que satisfacin la condició
existeix una funció ƒ que pertany a l'espai vectorial Lp(Ω) tal que
Imposant condicions de ser fitades, no només a la funció sinó també a les seves derivades porta als espais de Sobolev.[57]
Espais de Hilbert[modifica]

Els espais complets basats en un producte escalar es coneixen com Espais de Hilbert, en honor de David Hilbert.[58] L'Espai de Hilbert L²(Ω), amb el producte escalar definit com
- ,
on denota el conjugat de g(x).[59][nb 8] és un cas clau.
Per definició, en un Espai de Hilbert qualsevol successió de Cauchy convergeix a un límit. El recíproc, trobar una successió de funcions ƒn amb propietats adequades que aproxima en el límit una funció donada, és també molt important. Les anàlisis del tipus de l'aproximació Taylor, estableixen una aproximació de funcions diferenciables f per polinomis.[60] Pel teorema de Stone-Weierstrass, tota funció contínua en [a, b] es pot aproximar tan com es vulgui per un polinomi.[61] Una tècnica similar d'aproximació per funcions trigonomètriques s'anomena comunament desenvolupament en sèrie de Fourier, i s'aplica molt en enginyeria, vegeu més avall. De forma més general, i més conceptual, el teorema dona una descripció simple de quines "funcions bàsiques", o, en Espais de Hilbert abstractes, quins vectors base són suficients per generar un Espai de Hilbert H, en el sentit que la clausura de la seva expansió (és a dir, combinacions lineals finites i límits d'aquestes) és l'espai sencer. Aquests conjunts de funcions s'anomenen una base de H, la seva cardinalitat es coneix com la dimensió Hilbert.[nb 9] El teorema no només identifica les funcions base adequades per propòsits d'aproximació, sinó que juntament amb el procés de Gram-Schmidt també permet construir una base de vectors ortogonals.[62] Aquestes bases ortogonals són la generalització de Hilbert a espais de dimensió infinita dels eixos de coordenades en els espais euclidians de dimensió finita.
Les solucions a moltes equacions diferencials es poden interpretar en termes d'Espais de Hilbert. Per exemple, molts problemes de física i enginyeria porten a aquest tipus d'equacions i sovint les solucions amb propietats físiques particulars es fan servir com a funcions base, sovint ortogonals.[63] Un exemple en física és l'equació de Schrödinger de la mecànica quàntica que descriu el canvi de les propietats físiques al llarg del temps, per mitjà d'una equació diferencial en derivades parcials. Les solucions d'aquesta equació s'anomenen funcions d'ona.[64] Els valors definits per a certes propietats físiques com ara l'energia, o la quantitat de moviment, es corresponen amb valors propis d'un determinat operador diferencial (lineal) i les funcions d'ona associades s'anomenen estats propis. El teorema espectral descompon un operador compacte lineal que opera sobre funcions en una combinació lineal d'aquestes funcions pròpies i els seus valors propis.[65]
Àlgebres sobre cossos[modifica]

Els espais vectorials generals no posseeixen una operació de multiplicació. Un espai vectorial proveït amb un operador bilineal addicional que defineix la multiplicació de dos vectors és una àlgebra sobre un cos.[66] Moltes àlgebres provenen de funcions en algun objecte geomètric: com que es poden multiplicar funcions amb valors en un cos, aquestes entitats formen àlgebres. El teorema de Stone-Weierstrass esmentat abans, per exemple, depèn d'àlgebres de Banach que són alhora les dues coses, espais de Banach i àlgebres.
L'àlgebra commutativa fa molt ús d'anells de polinomis d'una o diverses variables, presentats més amunt. La seva multiplicació és tant commutativa com associativa. Aquests anells i els seus quocients formen la base de la geometria algebraica, perquè són anells de funcions d'objectes geomètrics algebraics.[67]
Un altre exemple crucial són les àlgebres de Lie, que no són ni commutatives ni associatives, però la manca de compliment d'aquestes propietats està limitada per les restriccions ([x, y] denota el producte de x per y):
Els exemples inclouen l'espai vectorial de matrius de n-per-n, amb [x, y] = xy − yx, el commutador de dues matrius, i R3, dotat del producte vectorial.
L'àlgebra tensorial T(V) és una manera formal d'afegir productes a qualsevol espai vectorial V per obtenir una àlgebra.[69] Com a espai vectorial, s'expandeix per símbols, anomenats tensors simples
- v1 ⊗ v₂ ⊗ ... ⊗ vn, en el grau n varia.
La multiplicació ve donada per la concatenació d'aquests símbols, imposant la propietat distributiva respecte de l'addició, i exigint que el producte per un escalar commuti amb el producte tensorial, de la mateixa manera com amb el producte tensorial de dos espais vectorials presentat més amunt. En general, no hi ha cap relació entre v1 ⊗ v₂ i v₂ ⊗ v1. Forçar que aquestes dues expressions siguin iguals porta a l'àlgebra simètrica, mentre que imposant v1 ⊗ v₂ = − v₂ ⊗ v1 porta a l'àlgebra exterior.[70]
Aplicacions[modifica]
Els espais vectorials tenen aplicacions múltiples atès que apareixen en moltes circumstàncies, arreu on hi hagi implicades funcions amb valors en algun cos. Proporcionen un marc per tractar problemes analítics i geomètrics, o es fan servir en la transformada de Fourier. Aquesta llista no és exhaustiva: hi ha moltes més aplicacions, per exemple en optimització. El teorema de minimax de teoria de jocs, que estableix l'existència d'un guany únic quan tots els jugadors juguen de manera òptima, es pot formular i demostrar fent servir mètodes d'espais vectorials.[71] La teoria de la representació trasllada profitosament la bona comprensió de l'àlgebra lineal i els espais vectorials a altres dominis matemàtics com la teoria de grups.[72]
Distribucions[modifica]
Una distribució (o funció generalitzada) és una aplicació lineal que assigna, de forma contínua, un nombre a cada funció de "prova", normalment una funció contínuament derivable amb suport compacte: en la terminologia de més amunt l'espai de distribucions és el dual (continu) de l'espai de funcions de prova.[73] Aquest últim espai està dotat amb una topologia que té en compte no només ƒ mateixa, sinó també totes les seves derivades d'ordre superior. Un exemple habitual és el resultat d'integrar una funció de prova ƒ sobre algun domini Ω:
Quan Ω = {p}, el conjunt format per un únic punt, es redueix a la distribució de Dirac, notada per δ, que associa a una funció de prova ƒ el seu valor a p: δ(ƒ) = ƒ(p). Les distribucions són un instrument potent per resoldre equacions diferencials. Com que totes les nocions analítiques habituals com les derivades són lineals, s'estenen de manera natural a l'espai de distribucions. Per això l'equació en qüestió es pot transferir a un espai de distribució, que és més gran que l'espai de funcions subjacent, de manera que hi ha mètodes més flexibles per resoldre l'equació. Per exemple, les funcions de Green i les solucions fonamentals habitualment són distribucions més que no pas funcions pròpiament dites, i llavors es poden fer servir per trobar solucions de l'equació amb les condicions de contorn imposades. Llavors de vegades es pot demostrar que la solució trobada és de fet una veritable funció, i una solució a l'equació original (per exemple, fent servir el teorema de Lax-Milgram, una conseqüència del teorema de representació de Riesz).[74]
Anàlisi de Fourier[modifica]

Expressar una funció periòdica com una suma de funcions trigonomètriques forma una sèrie de Fourier, que és una tècnica que es fa servir molt en física i en enginyeria.[nb 10][75] L'espai vectorial subjacent normalment és l'espai de Hilbert L²(0, 2π), per al qual les funcions sin mx i cos mx (m enter) formen una base ortogonal.[76] El desenvolupament en sèrie de Fourier d'una funció de L² f és
Els coeficients am i bm s'anomenen coeficients de Fourier de ƒ, i es calculen amb les fórmules[77]
- ,
En termes propis de la física la funció es representa com una superposició d'ones sinusoidals i els coeficients donen informació sobre l'espectre de freqüències de la funció.[78] Habitualment també es fa servir una forma d'expressar les sèries de Fourier basada en els nombres complexos.[77] Les fórmules concretes de damunt són les conseqüències d'una dualitat matemàtica més general anomenada dualitat de Pontryagin.[79] Aplicada al grup R, produeix la transformada clàssica de Fourier; una aplicació en física en són els reticles recíprocs, on el grup subjacent és un espai vectorial real de dimensió finita dotat de l'estructura addicional d'un reticle que codifica les posicions dels àtoms en els cristalls.[80]
Les sèries de Fourier es fan servir per resoldre problemes de condició de contorn en equacions diferencials en derivades parcials.[81] El 1822, Fourier va fer servir per prima vegada aquesta tècnica per resoldre l'equació de transferència de calor.[82] Una versió discreta de la Sèrie de Fourier es pot fer servir en aplicacions de mostratge en aplicacions de processament del senyal on el valor de funció es coneix només en un nombre finit de punts equiespaiats. En aquest cas la Sèrie de Fourier és finita i el seu valor en els punts de mostra coincideix amb els valors mesurats.[83] El conjunt de coeficients es coneix com la transformada discreta de Fourier (DFT) de la successió de mostra donada. La DFT és una de les eines clau del processament digital del senyal, un camp que s'aplica al radar, la codificació de veu, i la compressió d'imatges.[84] El format d'imatge de JPEG és una aplicació de la Transformada Cosinus Discreta que hi està relacionada de prop.[85]
La transformada ràpida de Fourier és un algorisme per calcular ràpidament la transformada discreta de Fourier.[86] Es fa servir no només per calcular els coeficients de Fourier sinó, utilitzant el teorema de convolució, també per calcular la convolució de dues successions finites.[87] Aquests mètodes s'apliquen en filtres digitals[88] i com a algorisme de multiplicació ràpid per a polinomis i enters grans (algorisme de Schönhage-Strassen).[89][90]
Geometria diferencial[modifica]

El pla tangent a una superfície a un punt és de manera natural un espai vectorial l'origen del qual s'identifica amb el punt de contacte. El pla tangent és la millor aproximació lineal, o linealització, d'una superfície a un punt.[nb 11] Fins i tot en un espai euclidià tridimensional, és impossible prescriure una base del pla de tangent d'una manera natural, atès que es defineix com un espai vectorial abstracte més que com un espai de coordenades real. L'espai tangent és la generalització a varietats diferenciables de dimensió superior.[91]
Les varietats Riemannianes són varietats els espais tangent de les quals es doten d'un producte intern adequat.[92] D'aquí s'obté el tensor de curvatura de Riemann, que codifica totes les curvatures d'una varietat en un objecte, cosa que té aplicacions en la relativitat general, per exemple, on el tensor de curvatura d'Einstein descriu la curvatura de l'espaitemps.[93][94] A l'espai tangent d'un grup de Lie se li pot donar de manera natural l'estructura d'una àlgebra de Lie i es pot fer servir per classificar els grups de Lie compactes.[95]
Generalitzacions[modifica]
Fibrat vectorial[modifica]
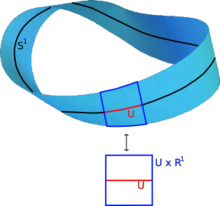
Un fibrat vectorial és una família d'espais vectorials parametritzada contínuament per un espai topològic X.[91] Més precisament, un fibrat vectorial sobre X és un espai topològic E proveït d'una aplicació contínua
- π : E → X
tal que, per a cada x de X, la fibra π−1(x) és un espai vectorial (real o complex). Quan les fibres tenen dimensió 1 s'anomena fibrat de línia. Per a qualsevol espai vectorial V (de dimensió finita), la projecció X × V → X dota el producte X × V d'una estructura de fibrat vectorial anomenat "trivial". Als fibrats vectorials sobre X se'ls exigeix que localment siguin un producte de X per algun espai vectorial (fixat) V: per a cada x de X, hi ha un veïnat obert U de x tal que la restricció de π a π−1(U)' és isomorf[nb 12] al fibrat trivial U × V → U. Malgrat el seu caràcter localment trivial, els fibrats vectorials poden (depenent de la forma de l'espai subjacent X) estar "torçats" a gran escala, és a dir, el fibrat no necessita ser "trivialitzable" (globalment isomorf al fibrat trivial X × V). Per exemple, la cinta de Möbius es pot veure com a fibrat de línia sobre la circumferència S¹. És, tanmateix, diferent del cilindre S¹ × R, perquè aquest últim és orientable mentre que l'anterior no ho és.[96]
Les propietats de certs fibrats vectorials proporcionen informació sobre l'espai topològic subjacent. Per exemple, el fibrat tangent d'una varietat diferenciable és la unió de tots els seus espais de tangents, parametritzada pels punts de la varietat. El fibrat tangent del cercle S¹ és globalment isomorf a S¹ × R, ja que hi ha un camp vectorial global no nul a S¹.[nb 13] En canvi, pel teorema de la bola peluda, no hi ha cap camp vectorial (tangent) en l'esfera S² que sigui diferent de zero arreu.[100] La teoria k estudia les classes d'isomorfisme de tots els fibrats vectorials sobre algun espai topològic.[97] A més d'aprofundir en els conceptes topològics i geomètrics, té conseqüències purament algebraiques, com ara la classificació de les àlgebres de divisió reals de dimensió finita: R, C, i H (els quaternions).
El fibrat cotangent d'una varietat diferenciable consta, en tots els punts de la varietat, del dual de l'espai de tangent, l'espai de cotangent. Les seccions d'aquest fibrat s'anomenen 1-formes diferencials.
Mòduls[modifica]
Els mòduls són als anells el que els espais vectorials als cossos. Exactament els mateixos axiomes, aplicats a un anell commutatiu R en comptes d'un cos K donen mòduls.[98] La teoria de mòduls, comparada amb la d'espais vectorials, es complica per la presència d'elements de l'anell que no tenen element invers de la multiplicació. Per exemple, els mòduls poden no tenir bases, com és el cas del Z-mòdul (és a dir el grup abelià) Z/2Z; els mòduls que en tenen (incloent-hi tots els espais vectorials) es coneixen com a mòduls lliures. La interpretació geomètrica dels anells commutatius mitjançant el seu espectre permet el desenvolupament de conceptes com els mòduls localment lliures, l'homòleg algebraic als fibrats vectorials.
Espais afí i projectiu[modifica]
Parlant informalment, els espais afins són espais vectorials l'origen dels quals no està especificat.[99] Més precisament, un espai afí és un conjunt amb una acció espacial vectorial transitiva lliure. En particular, un espai vectorial és un espai afí sobre si mateix, per l'aplicació
- V × V → V, (v, a) ↦ a + v.
Si W és un espai lineal, llavors un subespai afí és un subconjunt de W obtingut traslladant un subespai lineal V per un vector fix x ∈ W; aquest espai es nota x + V (és una classe lateral de V a W) i consta de tots els vectors de la forma x + v per a v ∈ V. Un exemple important és l'espai de solucions d'un sistema d'equacions lineals no homogènies
- Ax = b
generalitzant el cas homogeni b = 0 de més amunt.[100] L'espai de solucions és el subespai afí x + V on x és una solució particular de l'equació, i V és l'espai de solucions de l'equació homogènia (el nucli de A).
El conjunt d'espais unidimensionals d'un espai vectorial de dimensió finita fixada V es coneix com l'espai projectiu; es pot fer servir per a generalitzar la idea de paral·lelisme de rectes que s'intersequen en l'infinit.[101] Les Grassmannianes i les varietats bandera generalitzen això parametritzant subespais lineals de dimensió fixada k i banderes de subespais, respectivament.
Notes[modifica]
- ↑ Les funcions característiques dels intervals (de les quals n'hi ha una quantitat infinita) són linealment independents, per exemple.
- ↑ En anglès es diuen eigen values i eigen vectors perquè ha derivat de l'alemany "eigen", que vol dir propi.
- ↑ Roman 2005, cap. 8, pàg. 140. Vegeu també descomposició de Jordan–Chevalley.
- ↑ Alguns autors (com per exemple Roman 2005) trien de començar amb aquesta relació d'equivalència i en dedueixen la forma concreta de E/N a partir d'ella.
- ↑ Aquest requisit implica que la topologia dona lloc a una estructura uniforme, Bourbaki 1989, cap. II
- ↑ La desigualtat triangular per a |−|p la subministra la desigualtat de Minkowski. Per motius tècnics, per obtenir una norma i no només una seminorma, en el context de funcions, s'han de identificar les funcions que coincideixen quasi per a tot.
- ↑ "En la mesura de Lebesgue L² moltes funcions, en ser no fitades, no es poden integrar amb la integral clàssica de Riemann. Així, espais de funcions Riemann integrables podrien no ser complets respecte a la norma L², i no se'ls podria aplicar la descomposició ortogonal. Això mostra un dels avantatges de la integració de Lebesgue.", Dudley 1989, sect. 5.3, pàg. 125
- ↑ Per p ≠2, Lp(Ω) no és un espai de Hilbert.
- ↑ Una base d'un espai de Hilbert no és la mateixa cosa que una base en el sentit de l'àlgebra lineal de més amunt. Per distingir-les, a l'última se l'anomena una base de Hamel.
- ↑ Tot i que les sèries de Fourier són periòdiques, la tècnica es pot aplicar a qualsevol funció L² en un interval a base de considerar que la funció es repeteix periòdicament fora de l'interval. Vegeu Kreyszig 1988, p. 601
- ↑ Això és dir que (BSE-3 2001), el pla que passa pel punt de contacte P és tal que la distància d'un punt P1 de la superfície al pla és infinitesimalment petita comparada amb la distància de P1 a P en el límit quan P1 tendeix a P al llarg de la superfície.
- ↑ És a dir hi ha un homeomorfisme de π−1(U) en V × U que es restringeix a isomorfismes lineals entre fibres.
- ↑ Un fibrat de línia, com ara el fibrat tangent de S¹ és trivial si i només si hi ha una secció que no s'anul·la enlloc, vegeu Husemoller 1994, Corolari 8.3. Les seccions del fibrat tangent són precisament els camps vectorials.
Referències[modifica]
- ↑ Bourbaki 1969, cap. "Algèbre linéaire et algèbre multilinéaire", pàg. 78–91
- ↑ Bolzano 1804
- ↑ Möbius 1827
- ↑ Hamilton 1853
- ↑ Grassmann 2000
- ↑ (Peano 1888, IX)
- ↑ Banach 1922
- ↑ Dorier 1995, Moore 1995
- ↑ Lang 1987, cap. I.1
- ↑ e.g. Lang 1993, cap. XII.3., pàg. 335
- ↑ Vegeu més avall a l'article
- ↑ Lang 1987, cap. IX.1
- ↑ Lang 1987, cap. VI.3.
- ↑ Lang 2002, cap. V.1
- ↑ Lang 1987, cap. II.2., pàg. 47–48
- ↑ Roman 2005, Teorema 1.9, pàg. 43
- ↑ Blass 1984
- ↑ Halpern 1966, p. 670–673
- ↑ Artin 1991, Teorema 3.3.13
- ↑ Braun 1993, Tema 3.4.5, pàg. 291
- ↑ Stewart 1975, Proposició 4.3, pàg. 52
- ↑ Stewart 1975, Teorema 6.5, pàg. 74
- ↑ Roman 2005, cap. 2, pàg. 45
- ↑ Lang 1987, cap. IV.4, Corolari, pàg. 106
- ↑ Lang 1987, Exemple IV.2.6
- ↑ Lang 1987, cap. VI.6
- ↑ Halmos 1974, p. 28, Ex. 9
- ↑ Lang 1987, Teorema IV.2.1, pàg. 95
- ↑ Roman 2005, Tema. 2.5 i 2.6, pàg. 49
- ↑ Lang 1987, cap. V.1
- ↑ Lang 1987, cap. V.3., Corolari, pàg. 106
- ↑ Lang 1987, Teorema VII.9.8, pàg. 198
- ↑ Roman 2005, cap. 8, pàg. 135–156
- ↑ Lang 1987, cap. IX.4
- ↑ Roman 2005, cap. 1, pàg. 29
- ↑ Roman 2005, cap. 1, pàg. 35
- ↑ Roman 2005, cap. 3, pàg. 64
- ↑ Lang 1987, cap. IV.3.
- ↑ Roman 2005, cap. 2, pàg. 48
- ↑ Mac Lane 1998
- ↑ Roman 2005, cap. 1, pàg. 31–32
- ↑ Lang 2002, cap. XVI.1
- ↑ Roman 2005, Tema. 14.3. Vegeu també lema de Yoneda.
- ↑ Schaefer & Wolff 1999, pàg. 204–205
- ↑ Bourbaki 2004, cap. 2, pàg. 48
- ↑ Roman 2005, cap. 9
- ↑ Naber 2003, cap. 1.2
- ↑ Treves 1967
- ↑ Bourbaki 1987
- ↑ Kreyszig 1989, §4.11-5
- ↑ Kreyszig 1989, §1.5-5
- ↑ Choquet 1966, Proposició III.7.2
- ↑ Treves 1967, p. 34–36
- ↑ Lang 1983, Cor. 4.1.2, pàg. 69
- ↑ Treves 1967, cap. 11
- ↑ Treves 1967, Teorema 11.2, pàg. 102
- ↑ Evans 1998, cap. 5
- ↑ Treves 1967, cap. 12
- ↑ Dennery 1996, pàg.190
- ↑ Lang 1993, Tema. XIII.6, pàg. 349
- ↑ Lang 1993, Tema. III.1.1
- ↑ Choquet 1966, Lema III.16.11
- ↑ Kreyszig 1999, Capítol 11
- ↑ Griffiths 1995, Capítol 1
- ↑ Lang 1993, cap. XVII.3
- ↑ Lang 2002, cap. III.1, pàg. 121
- ↑ Eisenbud 1995, cap. 1.6
- ↑ Varadarajan 1974
- ↑ Lang 2002, cap. XVI.7
- ↑ Lang 2002, cap. XVI.8
- ↑ Luenberger 1997, Secció 7.13
- ↑ Vegeu teoria de la representació i representació de grup.
- ↑ Lang 1993, cap. XI.1
- ↑ Evans 1998, Tema. 6.2.1
- ↑ Folland 1992, pàg. 349 ff
- ↑ Gasquet & Witomski 1999, p. 150
- ↑ 77,0 77,1 Gasquet & Witomski 1999, §4.5
- ↑ Gasquet & Witomski 1999, p. 57
- ↑ Loomis 1953, cap. VII
- ↑ Ashcroft & Mermin 1976, cap. 5
- ↑ Kreyszig 1988, p. 667
- ↑ Fourier 1822
- ↑ Gasquet & Witomski 1999, p. 67
- ↑ Ifeachor & Jervis 2002, p. 3–4, 11
- ↑ Wallace Feb 1992
- ↑ Ifeachor & Jervis 2002, p. 132
- ↑ Gasquet & Witomski 1999, §10.2
- ↑ Ifeachor & Jervis 2002, p. 307–310
- ↑ Gasquet & Witomski 1999, §10.3
- ↑ Schönhage & Strassen 1971
- ↑ 91,0 91,1 Spivak 1999, cap. 3
- ↑ Jost 2005. Vegeu també varietat de Lorentz.
- ↑ Misner, Thorne & Wheeler 1973, cap. 1.8.7, pàg. 222 i cap. 2.13.5, pàg. 325
- ↑ Jost 2005, cap. 3.1
- ↑ Varadarajan 1974, cap. 4.3, Teorema 4.3.27
- ↑ Kreyszig 1991, §34, pàg. 108
- ↑ Eisenberg & Guy 1979
- ↑ Artin 1991, cap. 12
- ↑ Meyer 2000, Exemple 5.13.5, pàg. 436
- ↑ Meyer 2000, Exercici 5.13.15–17, pàg. 442
- ↑ Coxeter 1987
Bibliografia[modifica]
Àlgebra lineal[modifica]
- Artin, Michael. Algebra (en anglès). Prentice Hall, 1991. ISBN 978-0-89871-510-1.
- Blass, Andreas. «Existence of bases implies the axiom of choice». A: Axiomatic set theory (Boulder, Colorado, 1983) (en anglès). 31. Providence, R.I.: American Mathematical Society, 1984, p. 31–33 (Contemporary Mathematics).
- Brown, William A. Matrices and vector spaces (en anglès). Nova York: M. Dekker, 1991. ISBN 978-0-8247-8419-5.
- Castellet, M.; Llerena, I. Àlgebra lineal i geometria (en català). Bellaterra (Cerdanyola del Vallès) (ES): Universitat Autònoma de Barcelona, 1988, p. 302. ISBN 978-8474889437.
- Lang, Serge. Linear algebra (en anglès). Berlín, Nova York: Springer-Verlag, 1987. ISBN 978-0-387-96412-6.
- Lang, Serge. Algebra (en anglès). 211. Revised third. Nova York: Springer-Verlag, 2002 (Graduate Texts in Mathematics). ISBN 978-0-387-95385-4.
- Meyer, Carl D. matrixanalysis.com Matrix Analysis and Applied Linear Algebra (en anglès). Society for Industrial and Applied Mathematics (SIAM), 2000. ISBN 978-0-89871-454-8.
- Roman, Steven. Advanced Linear Algebra (en anglès). 135. 2a ed.. Berlín, Nova York: Springer-Verlag, 2005 (Graduate Texts in Mathematics). ISBN 978-0-387-24766-3.
- van der Waerden, Bartel Leendert. Algebra (en alemany). 9a ed.. Berlín, Nova York: Springer-Verlag, 1993. ISBN 978-3-540-56799-8.
Anàlisi[modifica]
- Bourbaki, Nicolas. Topological vector spaces (en anglès). Berlín, Nova York: Springer-Verlag, 1987 (Elements of mathematics). ISBN 978-3-540-13627-9.
- Bourbaki, Nicolas. Integration I (en anglès). Berlín, Nova York: Springer-Verlag, 2004. ISBN 978-3-540-41129-1.
- Braun, Martin. Differential equations and their applications: an introduction to applied mathematics (en anglès). Berlín, Nova York: Springer-Verlag, 1993. ISBN 978-0-387-97894-9.
- Choquet, Gustave. Topology (en anglès). Boston, MA: Academic Press, 1966.
- Dennery, Philippe; Krzywicki, Andre. Mathematics for Physicists (en anglès). Courier Dover Publications, 1996. ISBN 978-0-486-69193-0.
- Dudley, Richard M. Real analysis and probability (en anglès). Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, 1989 (The Wadsworth & Brooks/Cole Mathematics Series). ISBN 978-0-534-10050-6.
- Dunham, William. The Calculus Gallery (en anglès). Princeton University Press, 2005. ISBN 978-0-691-09565-3.
- Evans, Lawrence C. Partial differential equations (en anglès). Providence, R.I.: American Mathematical Society, 1998. ISBN 978-0-8218-0772-9.
- Folland, Gerald B. Fourier Analysis and Its Applications (en anglès). Brooks-Cole, 1992. ISBN 978-0-534-17094-3.
- Gasquet, Claude; Witomski, Patrick. Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets (en anglès). Nova York: Springer-Verlag, 1999 (Texts in Applied Mathematics). ISBN 0-387-98485-2.
- Ifeachor, Emmanuel C.; Jervis, Barrie W. Digital Signal Processing: A Practical Approach (en anglès). 2a edició. Harlow, Essex, England: Prentice-Hall, 2002. ISBN 0-201-59619-9.
- Krantz, Steven G. A Panorama of Harmonic Analysis (en anglès). Washington, DC: Mathematical Association of America, 1999 (Carus Mathematical Monographs). ISBN 0-88385-031-1.
- Kreyszig, Erwin. Advanced Engineering Mathematics (en anglès). 6a ed.. Nova York: John Wiley & Sons, 1988. ISBN 0-471-85824-2.
- Kreyszig, Erwin. Introductory functional analysis with applications (en anglès). Nova York: John Wiley & Sons, 1989 (Wiley Classics Library). ISBN 978-0-471-50459-7.
- Lang, Serge. Real analysis (en anglès). Addison-Wesley, 1983. ISBN 978-0-201-14179-5.
- Lang, Serge. Real and functional analysis (en anglès). Berlín, Nova York: Springer-Verlag, 1993. ISBN 978-0-387-94001-4.
- Loomis, Lynn H. An introduction to abstract harmonic analysis (en anglès). Toronto-Nova York-Londres: D. Van Nostrand Company, Inc., 1953, p. x+190.
- Schaefer, Helmut H.; Wolff, M.P.. Topological vector spaces (en anglès). 2a ed.. Berlín, Nova York: Springer-Verlag, 1999. ISBN 978-0-387-98726-2.
- Treves, François. Topological vector spaces, distributions and kernels (en anglès). Boston, MA: Academic Press, 1967.
Referències històriques[modifica]
- Banach, Stefan «matwbn.icm.edu Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)» (en francès). Fundamenta Mathematicae, 3, 1922. ISSN: 0016-2736.
- Bolzano, Bernard. Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) (en alemany), 1804.
- Bourbaki, Nicolas. Éléments d'histoire des mathématiques (Elements of history of mathematics) (en francès). París: Hermann, 1969.
- Dorier, Jean-Luc «A general outline of the genesis of vector space theory» (en anglès). Historia Mathematica, 22, 3, 1995, pàg. 227–261. ISSN: 0315-0860.
- Fourier, Jean Baptiste Joseph. Théorie analytique de la chaleur (en francès). Chez Firmin Didot, père et fils, 1822.
- Grassmann, Hermann. Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik, 1844., reprint: Kannenberg, L.C.. Extension Theory (en alemany). Providence, R.I.: American Mathematical Society, 2000. ISBN 978-0-8218-2031-5.
- Hamilton, William Rowan. Lectures on Quaternions (en anglès). Royal Irish Academy, 1853.
- Möbius, August Ferdinand. Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) (en alemany), 1827 [Consulta: 17 març 2009].
- Moore, Gregory H. «The axiomatization of linear algebra: 1875-1940» (en anglès). Historia Mathematica, 22, 3, 1995, pàg. 262–303. ISSN: 0315-0860.
- Peano, Giuseppe. Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (en italià), 1888.
Bibliografia addicional[modifica]
- Ashcroft, Neil; Mermin, N. David. Solid State Physics. Toronto: Thomson Learning, 1976. ISBN 978-0-03-083993-1.
- Atiyah, Michael Francis. K-theory. 2a ed.. Addison-Wesley, 1989 (Advanced Book Classics). ISBN 978-0-201-09394-0.
- Bourbaki, Nicolas. General Topology. Chapters 1-4. Berlín, Nova York: Springer-Verlag, 1989. ISBN 978-3-540-64241-1.
- Coxeter, Harold Scott MacDonald. Projective Geometry. 2a ed.. Berlín, Nova York: Springer-Verlag, 1987. ISBN 978-0-387-96532-1.
- Eisenberg, Murray; Guy, Robert «A proof of the hairy ball theorem». American Mathematical Monthly, 86, 7, 1979, pàg. 572–574. ISSN: 0002-9890.
- Eisenbud, David. Commutative algebra. 150. Berlín, Nova York: Springer-Verlag, 1995 (Graduate Texts in Mathematics). ISBN 978-0-387-94268-1; 978-0-387-94269-8.
- Goldrei, Derek. Classic Set Theory: A guided independent study. 1a ed.. Londres: Chapman and Hall, 1996. ISBN 0-412-60610-0.
- Griffiths, David J. Introduction to Quantum Mechanics. Upper Saddle River, NJ: Prentice Hall, 1995. ISBN 0-13-124405-1.
- Halmos, Paul R. Finite-dimensional vector spaces. Berlín, Nova York: Springer-Verlag, 1974. ISBN 978-0-387-90093-3.
- Halpern, James D. «Bases in Vector Spaces and the Axiom of Choice». Proceedings of the American Mathematical Society, 17, 3, juny, pàg. 670–673. ISSN: 0002-9939.
- Husemoller, Dale. Fibre Bundles. 3a ed.. Berlín, Nova York: Springer-Verlag, 1994. ISBN 978-0-387-94087-8.
- Jost, Jürgen. Riemannian Geometry and Geometric Analysis. 4a ed.. Berlín, Nova York: Springer-Verlag, 2005. ISBN 978-3-540-25907-7.
- Kreyszig, Erwin. Differential geometry. Nova York: Dover Publications, 1991, p. xiv+352. ISBN 978-0-486-66721-8.
- Kreyszig, Erwin. Advanced Engineering Mathematics. 8a ed.. Nova York: John Wiley & Sons, 1999. ISBN 0-471-15496-2.
- Luenberger, David. Optimization by vector space methods. Nova York: John Wiley & Sons, 1997. ISBN 978-0-471-18117-0.
- Mac Lane, Saunders. Categories for the Working Mathematician. 2a ed.. Berlín, Nova York: Springer-Verlag, 1998. ISBN 978-0-387-98403-2.
- Misner, Charles W.; Thorne, Kip; Wheeler, John Archibald. Gravitation. W. H. Freeman, 1973. ISBN 978-0-7167-0344-0.
- Naber, Gregory L. The geometry of Minkowski spacetime. Nova York: Dover Publications, 2003. ISBN 978-0-486-43235-9.
- Schönhage, A.; Strassen, Volker «Schnelle Multiplikation großer Zahlen (Fast multiplication of big numbers)» (en alemany). Computing, 7, 1971, pàg. 281–292. ISSN: 0010-485X.[Enllaç no actiu]
- Spivak, Michael. A Comprehensive Introduction to Differential Geometry (volum II). Houston, TX: Publish or Perish, 1999.
- Stewart, Ian. Galois Theory. Londres: Chapman and Hall, 1975 (Chapman and Hall Mathematics Series). ISBN 0-412-10800-3.
- Varadarajan, V. S.. Lie groups, Lie algebras, and their representations. Prentice Hall, 1974. ISBN 978-0-13-535732-3.
- Wallace, G.K. «The JPEG still picture compression standard». IEEE Transactions on Consumer Electronics, 38, 1, Feb 1992, pàg. xviii–xxxiv. ISSN: 0098-3063.
- Weibel, Charles A. An introduction to homological algebra. 38. Cambridge University Press, 1994 (Cambridge Studies in Advanced Mathematics). ISBN 978-0-521-55987-4. OCLC 36131259.
Vegeu també[modifica]














































![{\displaystyle \left[x,\,y\right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b9c30c14c4467a1cf333f6c36311905586864cb)
![{\displaystyle -\left[y,\,x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ef2811abeaedf613274d4c0ace200248ac35b66)
![{\displaystyle \left[x,\,[y,z]\,\right]+\left[y,\,[z,x]\,\right]+\left[z,\,[x,y]\,\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91cff8fd3ebba04b1a5ad3573fce571d27521caf)

![{\displaystyle {\frac {a_{0}}{2}}+\sum _{m=1}^{\infty }\left[a_{m}\cos \left(mx\right)+b_{m}\sin \left(mx\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b02fb26ebada4babaa1d88e20bb63e3b370c13b3)

