Sèrie de Taylor


En matemàtiques, i més específicament en càlcul infinitesimal, la sèrie de Taylor és una representació d'una funció com una suma infinita de termes calculats a partir dels valors de les derivades de la funció en un punt concret. Més concretament, si és una funció de variable real, infinitament diferenciable en el veïnat d'un punt , aleshores la seva sèrie de Taylor centrada en a és la sèrie de potències següent:
- .
El concepte de sèrie de Taylor va ser introduït formalment pel matemàtic anglès Brook Taylor l'any 1715. Quan la sèrie de Taylor està centrada al zero, llavors també s'anomena sèrie de Maclaurin, en honor del matemàtic escocès Colin Maclaurin, qui feu un ús extensiu d'aquest cas especial de la sèrie de Taylor al s. XVIII.
Quan una funció té un grau de diferenciabilitat finit, o quan es vol fer un càlcul numèric del valor de la funció en les proximitats d'un punt, llavors s'usa el polinomi de Taylor, que és el mateix que la sèrie però amb només un nombre finit de termes. En aquest cas el teorema de Taylor dona estimacions quantitatives de l'error que es comet amb aquest tipus d'aproximació. Es pot considerar que la sèrie de Taylor és el límit dels polinomis de Taylor quan el grau tendeix a infinit.
Encara que una funció sigui infinitament diferenciable en un veïnat de a, pot passar que la seva sèrie de Taylor tingui radi de convergència zero, la qual cosa significa que la sèrie no es pot avaluar en cap punt diferent de . També pot passar que el radi de convergència sigui més gran que zero, però que la sèrie no coincideixi amb la funció en cap punt diferent de a. Una funció que és igual a la seva sèrie de Taylor en un cert domini s'anomena funció analítica.
Definició[modifica]
La sèrie de Taylor d'una funció real o complexa que sigui infinitament diferenciable en un veïnat d'un nombre (real o complex) a és la sèrie de potències següent:[1]
Aquesta sèrie es pot escriure d'una manera més compacta fent servir el sumatori com:
on denota el factorial de i denota la derivada -èsima de avaluada en el punt . S'entén que la derivada d'ordre zero de és la pròpia , i i valen, ambdós, 1. En el cas que , la sèrie també s'anomena sèrie de MacLaurin.
Història[modifica]
El concepte de sèrie de Taylor, i de sèrie de potències, està estretament lligat al de sèrie numèrica. El problema de la suma d'una sèrie infinita de nombres ja fou estudiat al s. V aC a l'antiga Grècia, però no fou fins al s. III aC quan Arquimedes donà un primer mètode de suma, el mètode d'exhaustió.[2] Els primers desenvolupaments en sèrie de potències podrien ser deguts al matemàtic indi Madhava de Sangamagrama (c. 1340-1425), fundador de l'Escola de Kerala, que obtingué les sèries de potències d'algunes funcions trigonomètriques: sinus, cosinus i arc tangent.[3] [4] Aquestes sèries foren redescobertes força més tard, al s. XVII, per Isaac Newton i James Gregory, mentre que Johannes Hudde i Nicolaus Mercator obtingueren la sèrie de Taylor del logaritme.[5]
L'any 1715 el matemàtic anglès Brook Taylor donà el mètode general per construir aquestes sèries de potències.[6] La sèrie de Taylor s'anomena en honor seu, i la sèrie de Maclaurin en honor del matemàtic escocès Colin Maclaurin, que publicà el cas especial del resultat de Taylor durant el s. XVIII.
Exemples[modifica]
La sèrie de Maclaurin (sèrie de Taylor centrada al zero) de qualsevol polinomi és el polinomi mateix.
La sèrie de Maclaurin de la funció és la sèrie geomètrica infinita
i la sèrie de Taylor de centrada en és
Si s'integren aquestes sèries s'obté la sèrie de Taylor de la funció , on denota el logaritme natural:
i la sèrie de Taylor corresponent per a centrada en , que és
La sèrie de Taylor de la funció exponencial centrada en és:
El desenvolupament anterior s'obté fàcilment, ja que la derivada de és , i val 1, la qual cosa deixa els termes al numerador i al denominador, per a cada terme de la suma infinita.
Funcions analítiques[modifica]

Si la funció ve donada per una sèrie de potències convergent en un disc obert (o interval en la recta real) centrat en , es diu que la funció és analítica dins d'aquest disc. Llavors, per una d'aquest disc, ve donada per la sèrie de potències convergent següent:
- .
Diferenciant la fórmula anterior respecte vegades i establint s'obté:
- .
Per la qual cosa l'expansió de la sèrie de potències es correspon amb la sèrie de Taylor. En conclusió, una funció és analítica en un disc obert centrat en b si i només si la seva sèrie de Taylor convergeix al valor de la funció en cada punt del disc.
Si f(x) equival a la seva sèrie de Taylor en qualsevol punt, s'anomena funció entera. Els polinomis, la funció exponencial ex i les funcions trigonomètriques sinus i cosinus són exemples de funcions enteres; per contra, algunes funcions que no són enteres són, per exemple, el logaritme, la tangent i l'arctangent. Per aquestes darreres funcions, la sèrie de Taylor no convergeix si x es troba lluny de b. La sèrie de Taylor es pot fer servir per calcular el valor d'una funció entera en qualsevol punt si el valor de la funció –i de totes les seves derivades– es coneixen per un punt concret.
Alguns usos de la sèrie de Taylor per funcions analítiques són els següents:
- Les sumes parcials (els polinomis de Taylor) de la sèrie es pot fer servir com aproximacions de la funció entera. Aquestes aproximacions són bones si s'hi inclouen suficients termes.
- La diferenciació i integració de sèries de potències es pot dur a terme terme a terme, per la qual cosa és especialment fàcil.
- Una funció analítica és únicament estesa a una funció holomorfa en un disc obert del pla complex, la qual cosa condueix a la possibilitat de l'anàlisi complexa.
- La sèrie (truncada) es pot fer servir per calcular numèricament valors de funcions. Sovint es fa transformant el polinomi a la forma de Txebixev i avaluant-lo amb l'algorisme de Clenshaw.
- Les operacions algebraiques es poden fer fàcilment sobre la representació en forma de sèrie de potències; per exemple, la fórmula d'Euler surt de l'expansió de la sèrie de Taylor de funcions trigonomètriques i exponencials. Aquest resultat resulta d'una importància fonamental en camps com l'anàlisi harmònica.
- Les aproximacions fetes fent servir pocs primers termes de la sèrie de Taylor poden convertir problemes que no podrien ser resolts en problemes possibles en un domini restringit. Aquest tipus d'aproximacions són freqüents en física.
Aproximació i convergència[modifica]
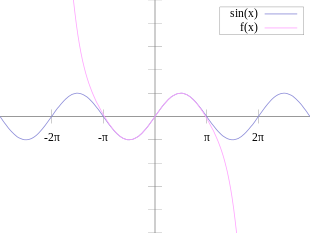

La imatge de la dreta mostra una aproximació acurada de la funció al voltant del punt . La corba rosa és el polinomi de Taylor de grau set:
- .
L'error d'aquesta aproximació no és superior a . En particular, per , l'error és inferior a 0,000003.
En contrast, la imatge inferior mostra la funció del logaritme i alguns dels seus polinomis de Taylor al voltant de . Aquestes aproximacions convergeixen cap a la funció tan sols en l'interval ; fora d'aquest, els polinomis de Taylor de grau superior són aproximacions pitjors de la funció. Això és similar al fenomen de Runge.
L'error que s'obté en aproximar una funció pel seu polinomi de Taylor de grau n s'anomena el residu i es denota per la funció . Es pot utilitzar el teorema de Taylor per obtenir un rang de la mida del residu.
En general, la sèrie de Taylor no ha de ser necessàriament convergent. De fet, el conjunt de funcions que tenen sèrie de Taylor convergent és un conjunt magre de l'espai de Fréchet de les funcions contínuament diferenciables. Fins i tot si la sèrie de Taylor d'una funció convergeix, el seu límit, en general, no ha de ser necessàriament igual al valor de la funció . Per exemple:
Aquesta funció és infinitament diferenciable en , i en aquest punt totes les seves derivades són nul·les. Conseqüentment, la sèrie de Taylor de al voltant de és idènticament zero. Tanmateix, no és igual a la funció zero i, per tant, tampoc no és igual a la seva sèrie de Taylor al voltant de l'origen.
En anàlisi real, aquest exemple demostra que hi ha funcions infinitament diferenciables que tenen sèries de Taylor que no són iguals a , fins i tot encara que convergeixin. D'altra banda, en anàlisi complexa no hi ha cap funció holomorfa que la seva sèrie de Taylor convergeixi a un valor diferent de . La funció complexa no s'aproxima a 0 quan s'aproxima a 0 al llarg de l'eix imaginari i, per tant, la seva sèrie de Taylor aquí no es troba definida.
D'una manera més general, tota seqüència de nombres reals o complexos pot aparèixer com a coeficients d'una sèrie de Taylor d'una funció infinitament diferenciable definida en la recta real; això és conseqüència del lema de Borel. Com a resultat, el radi de convergència d'una sèrie de Taylor pot ser zero. Fins i tot hi ha funcions infinitament diferenciables definides en la recta real les sèries de Taylor de les quals tenen un radi de convergència nul a tot arreu.[7]
Algunes funcions no es poden escriure en forma de sèrie de Taylor perquè tenen una singularitat; tot i això, en aquests casos es pot aconseguir una expansió en forma de sèrie si es permeten potències negatives de (vegeu Sèrie de Laurent). Per exemple, es pot escriure com una sèrie de Laurent.
Generalització[modifica]
Existeix una generalització de la sèrie de Taylor que convergeix al valor de la mateixa funció per qualsevol funció contínua fitada en , fent servir el càlcul de diferències finites.[8][9] El següent teorema, enunciat per Einar Hille, postula que per qualsevol ,
Aquí, és l'operador diferència finita -èsima de mida de pas . La sèrie és precisament la sèrie de Taylor, excepte pel fet que apareixen les diferències dividides en comptes de la diferenciació: la sèrie és formalment similar a la sèrie de Newton. Quan la funció és analítica en , els termes de la sèrie convergeixen als termes de la sèrie de Taylor, és a dir, generalitzen aquesta darrera.
En general, per qualsevol seqüència infinita ai, es manté la següent identitat de sèrie de potències:
Per tant, en particular,
La sèrie de la dreta és el valor esperat de , on és una variable aleatòria que segueix la distribució de Poisson i que pren el valor amb probabilitat Llavors,
La llei dels grans nombres fa que es mantingui aquesta identitat.
Llista de sèries de Maclaurin d'algunes funcions comunes[modifica]



A continuació es mostren diverses expansions de sèries de Maclaurin de funcions importants.[10][1] Totes les expansions són vàlides per arguments complexos.
Sèrie geomètrica finita:
Sèrie geomètrica infinita:
Variants de la sèrie geomètrica infinita:
Sèrie binomial (inclou l'arrel quadrada per i la sèrie geomètrica infinita per ):
amb coeficients binomials generalitzats
Els nombres que apareixen en les expansions del sumatori de i són els nombres de Bernoulli. Els en l'expansió de són nombres d'Euler.
Càlcul de la sèrie de Taylor[modifica]
Existeixen molts mètodes per calcular la sèrie de Taylor d'un gran nombre de funcions. Es pot intentar fer servir la sèrie de Taylor tal com és i generalitzar la forma dels coeficients directament, o bé es poden utilitzar manipulacions com la substitució, multiplicació, divisió, addició o subtracció de la sèrie de Taylor estàndard per construir la sèrie de Taylor d'una funció (això és possible perquè la sèrie de Taylor és una sèrie de potències). En alguns casos, també es pot obtenir la sèrie de Taylor aplicant repetidament la integració per parts. Un mètode particularment útil de calcular la sèrie de Taylor són els sistemes algebraics computacionals.
Primer exemple[modifica]
Es vol calcular el polinomi de Taylor (o de MacLaurin) de grau 7 per la funció
- .
Primer, es reescriu la funció com
- .
Pel logaritme es té que (fent servir la notació de Landau o notació d'O gran)
i per la funció cosinus
La darrera expansió de la sèrie té un terme constant igual a zero, la qual cosa permet substituir la segona sèrie dins de la primera i ometre els termes d'ordre superior que els de grau 7 fent servir la notació de Landau:
Com que el cosinus és una funció parella, els coeficients de totes les potències imparelles han de ser zero.
Segon exemple[modifica]
Es vol obtenir la sèrie de Taylor centrada en 0 de la funció
- .
Per una funció exponencial es té que
i, igual que en el primer exemple,
S'assumeix que la sèrie de potències és
Llavors, si es multiplica amb el denominador i se substitueix la sèrie del cosinus s'obté
Agrupant termes fins a l'ordre quatre dona
Finalment, si es comparen els coeficients amb la sèrie de la funció exponencial, s'obté la sèrie de Taylor desitjada:
Tercer exemple[modifica]
En aquest cas es fa servir un mètode anomenat «expansió indirecta» per aconseguir expandir la funció donada. Es vol expandir la següent funció en forma d'una sèrie de potències de :
- .
Se sap que la sèrie de Taylor de la funció és
Llavors,
Sèrie de Taylor com a definició[modifica]
Clàssicament, les funcions algebraiques es defineixen per una equació algebraica, i les funcions transcendents es defineixen per alguna propietat que satisfacin, com ara una equació diferencial. Per exemple, la funció exponencial és la funció que és igual a la seva pròpia derivada en qualsevol punt, i assumeix el valor 1 a l'origen. També es pot definir una funció analítica per la seva sèrie de Taylor.
La sèrie de Taylor es fa servir per definir funcions i «operadors» en diverses àrees de les matemàtiques. Particularment, això és cert en àrees en les quals les definicions clàssiques de les funcions no es compleixen. Per exemple, es poden definir –fent servir la sèrie de Taylor– funcions analítiques de matrius i operadors tals com l'exponencial d'una matriu o el logaritme d'una matriu.
En altres àrees, com per exemple l'anàlisi formal, és més convenient treballar directament amb la mateixa sèrie de potències. Llavors, es pot definir una solució d'una equació diferencial com una sèrie de potències que, tal com es vol demostrar, és la sèrie de Taylor de la solució desitjada.
Sèrie de Taylor de diverses variables[modifica]
La sèrie de Taylor també es pot generalitzar per funcions de més d'una variable amb:
Per exemple, per una funció que depèn de dues variables i , la sèrie de Taylor de segon ordre al voltant del punt és:
Els subíndexs denoten les derivades parcials respectives.
Una expansió de segon ordre de la sèrie de Taylor d'una funció escalar de més d'una variable es pot escriure de manera compacta com:
on és el gradient de avaluat en i és la matriu hessiana. Si s'aplica la notació multiíndex, la sèrie de Taylor per diverses variables esdevé:
Aquesta forma s'ha d'entendre com una versió multiíndex encara més abreujada de la primera equació d'aquesta secció, de nou en analogia completa amb el cas d'una sola variable.
Exemple[modifica]

Es vol calcular l'expansió de la sèrie de Taylor de segon ordre al voltant del punt de la funció
En primer lloc, cal calcular totes les derivades parcials necessàries:
La sèrie de Taylor és:
Que en aquest cas esdevé:
com que és analític en, es té que:
per .
Sèrie de Taylor fraccionària[modifica]
Amb l'emergència del càlcul fraccionari es planteja la pregunta de com seria el desenvolupament de la sèrie de Taylor. Odibat i Shawagfeh[11] van donar-ne la resposta el 2007. Si es fa servir la derivada fraccionària de Caputo, , i indica el límit en aproximar-se per la dreta, la sèrie de Taylor fraccionària es pot escriure com:
Comparació amb la sèrie de Fourier[modifica]
La sèrie de Fourier trigonomètrica permet expressar una funció periòdica (o una funció definida en un interval compacte) en una suma infinita de funcions trigonomètriques (sinus i cosinus).[12] En aquest sentit, la sèrie de Fourier es pot considerar anàloga a la sèrie de Taylor, ja que aquesta permet expressar una funció com a suma infinita de potències. Tanmateix els dos tipus de sèrie difereixen en qüestions fonamentals:
- El càlcul de la sèrie de Taylor requereix el coneixement de la funció en un veïnat arbitràriament petit d'un punt, mentre que el càlcul de la sèrie de Fourier requereix conèixer la funció en tot el seu interval de domini. En certa manera es podria dir que la sèrie de Taylor és «local» i la sèrie de Fourier «global».
- El càlcul de la sèrie de Taylor requereix que la funció sigui de classe , mentre que el de la sèrie de Fourier només requereix que la funció sigui integrable (i doncs ni cal que sigui contínua).
- La convergència de les dues sèries té propietats molt diferents. Encara que la sèrie de Taylor tingui radi de convergència estrictament positiu, la sèrie resultant pot no coincidir amb la funció; però si la funció és analítica, aleshores la sèrie convergeix puntualment a la funció, i uniformement en cada conjunt compacte. Pel que fa a la sèrie de Fourier, si la funció és de quadrat integrable aleshores la sèrie convergeix en mitjana quadràtica; però calen requisits addicionals per assegurar la convergència puntual o la uniforme (per exemple, si la funció és periòdica i de classe aleshores la convergència és uniforme).
- Finalment, a la pràctica es vol aproximar la funció amb un nombre finit de termes, ja sigui el polinomi de Taylor o una suma parcial de la sèrie trigonomètrica, respectivament. En el cas de la sèrie de Taylor l'error és molt petit en un veïnat del punt on es calcula, mentre que l'error pot ser molt gran en un punt allunyat. En el cas de la sèrie de Fourier l'error està distribuït per tot el domini de la funció.
Referències[modifica]
- ↑ 1,0 1,1 Weisstein, Eric W., «Taylor Series» a MathWorld (en anglès).
- ↑ Kline, M. (1990) Mathematical Thought from Ancient to Modern Times. Oxford University Press. pp. 35-37.
- ↑ Roy, Ranjan. Sources in the development of mathematics. Cambdridge: Cambridge University Press, 2011. ISBN 978-0-521-11470-7., pàg. 3
- ↑ Dani, S. G. «Ancient Indian Mathematics – A Conspectus». Resonance, 17, 2012, pàg. 236-246.
- ↑ Roy, Ranjan. Sources in the development of mathematics. Cambdridge: Cambridge University Press, 2011. ISBN 978-0-521-11470-7., pàg. 140
- ↑ Taylor, Brook. Methodus Incrementorum Directa et Inversa, 1715.; pàg 21-23, proposició VII, teorema 3, corol·lari 2
- ↑ Rudin, Walter. McGraw-Hill. Real and Complex Analysis, 1980, p. 418, exercici 13. ISBN 0-07-099557-5.
- ↑ Feller, William. An introduction to probability theory and its applications, Volume 2. 3a edició. Wiley, 1971, p. 230-232.
- ↑ Hille, Einar; Phillips, Ralph S. Functional analysis and semi-groups. 31. American Mathematical Society, 1957, p. 300-327 (AMS Colloquium Publications).
- ↑ La majoria es poden trobar a: (Abramowitz & Stegun 1970)
- ↑ Odibat, ZM.; Shawagfeh, NT. «186». A: Generalized Taylor's formula. Applied Mathematics and Computation (en anglès), 2007, p. 286-293.
- ↑ Weisstein, Eric W., «Fourier Series» a MathWorld (en anglès).
Bibliografia[modifica]
- Abramowitz, Milton; Stegun, Irene A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (en anglès). Nova York: Dover Publications, 1970.
- Thomas, George B. Jr.; Finney, Ross L. Calculus and Analytic Geometry (en anglès). 9a ed. Addison Wesley, 1996. ISBN 0-201-53174-7.
- Greenberg, Michael. Advanced Engineering Mathematics (en anglès). 2a ed. Prentice Hall, 1998. ISBN 0-13-321431-1.
Vegeu també[modifica]
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Sèrie de Taylor |
- Michiel Hazewinkel (ed.). Taylor series. Encyclopedia of Mathematics (en anglès). Springer, 2001. ISBN 978-1-55608-010-4.
- Representació de la sèrie de Taylor per John H. Mathews (anglès)
- Una altra visualització de la sèrie de Taylor Arxivat 2007-06-05 a Wayback Machine. en la qual es pot escollir el punt d'aproximació i el nombre de derivades (anglès)
- Taylor series revisited for numerical methods a Numerical Methods for the STEM Undergraduate (anglès)
- Sèrie de Taylor de funcions trigonomètriques inverses (anglès)
- Matlab- Expansió en sèries de Taylor Arxivat 2013-06-24 a Wayback Machine. (anglès)











































































































![{\displaystyle {\begin{aligned}f(x,y)&\approx f(a,b)+(x-a)\,f_{x}(a,b)+(y-b)\,f_{y}(a,b)\\&{}\quad +{\frac {1}{2!}}\left[(x-a)^{2}\,f_{xx}(a,b)+2(x-a)(y-b)\,f_{xy}(a,b)+(y-b)^{2}\,f_{yy}(a,b)\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf9ea2f461197849d805af5c7120ad0f6a3a1b72)














![{\displaystyle {\begin{aligned}T(x,y)=f(a,b)&+(x-a)\,f_{x}(a,b)+(y-b)\,f_{y}(a,b)\\&+{\frac {1}{2!}}\left[(x-a)^{2}\,f_{xx}(a,b)+2(x-a)(y-b)\,f_{xy}(a,b)+(y-b)^{2}\,f_{yy}(a,b)\right]+\cdots \,,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83637bd427241854df42cc15345d6683b3e09887)
![{\displaystyle {\begin{aligned}T(x,y)&=0+0(x-0)+1(y-0)+{\frac {1}{2}}{\Big [}0(x-0)^{2}+2(x-0)(y-0)+(-1)(y-0)^{2}{\Big ]}+\cdots \\&=y+xy-{\frac {y^{2}}{2}}+\cdots .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/620c279c9d7f3f4c1fca3546c7cb3e5ee3b31f53)







