Funció trigonomètrica
En matemàtiques, les funcions trigonomètriques són funcions d'un angle. Són la base per l'estudi de la trigonometria, els triangles i per la modelització dels fenòmens periòdics, entre moltes altres aplicacions. Les funcions trigonomètriques es defineixen habitualment com a quocients entre les longituds de dos costats d'un triangle rectangle que contingui l'angle, i de forma equivalent es poden definir a partir de les longituds de diversos segments a partir de la circumferència goniomètrica (circumferència de radi unitat, el centre de la qual és l'origen d'un sistema de coordenades cartesianes). Hi ha definicions més modernes que les expressen com a sèries infinites o com a solucions d'equacions diferencials; l'avantatge d'aquestes definicions és que permeten estendre les funcions trigonomètriques a cossos arbitraris com per exemple els nombres complexos.
Actualment es fan servir les sis funcions trigonomètriques que es presenten a la taula de la dreta, juntament amb algunes de les identitats que permeten calcular-ne unes a partir de les altres. En el cas de les últimes quatre funcions trigonomètriques, sovint es prenen aquestes identitats com a "definicions" de les mateixes funcions, però es poden definir perfectament de manera geomètrica, o per altres mitjans, i llavors demostrar aquestes identitats. De fet, tal com s'aprecia a les identitats de la taula, només cal definir-ne una qualsevol i després es poden emprar unes o altres identitats per definir i calcular tota la resta.
| Funció | Abreviació | Identitats (emprant radiants) |
|---|---|---|
| Sinus | sin | |
| Cosinus | cos | |
| Tangent | tan (o tg) |
|
| Cosecant | csc (o cosec) |
|
| Secant | sec | |
| Cotangent | cot (o ctg o ctn) |
Història[modifica]
La noció que hi ha d'haver alguna correspondència bàsica entre la longitud de les cares d'un triangle i els angles apareix tan aviat com en reconeix que els triangles semblants mantenen constants les relacions entre les seves cares. És a dir, per a qualsevol triangle rectangle semblant a un de donat, la relació (el quocient entre les longituds) entre la hipotenusa (per exemple) i una altra de les seves cares es manté constant. Si la hipotenusa és el doble de llarga, també ho són les altres dues cares. Són precisament aquestes relacions les que es fan servir per a expressar les funcions trigonomètriques.
Les funcions trigonomètriques varen ser estudiades per:
- El matemàtic grec Hiparc de Nicea (180-125 AC) va crear taules on relacionava la longitud de l'arc amb la longitud de la corda corresponent,[1]
- A Egipte, Claudi Ptolemeu (90–180 AD) va escriure l'almagest on desenvolupa les fórmules equivalents a les actuals pel sinus de la suma de dos angles però per la funció corda, i una fórmula pel càlcul de la corda de l'angle meitat, a partir d'aquí va crear una taula trigonomètrica[2]
- El matemàtic Indi Aryabhata (476–550) definí per primera vegada les funcions sinus (la meitat de la corda) i cosinus. Els seus treballs contenen les taules més antigues que existeixin actualment dels valors del sinus de tots els angles compresos entre 0° i 90° a intervals de 3,75°, amb una precisió de 4 decimals. Aquesta taula fou reproduïda per Brahmagupta (628)[1]
- Segons l'obra d'Abu l-Wafa, sembla que els matemàtics musulmans utilitzaven cadascuna de les sis funcions trigonomètriques, i disposaven de taules amb intervals de 0,25°, amb 8 decimals exactes.[3]
- El matemàtic català Savasorda (1070-1136) escriu la primera taula trigonomètrica en llatí. Aquesta taula fa servir la corda seguint la tradició clàssica en comptes del sinus que empraven els àrabs, divideix la circumferència goniomètrica en 88 parts (en comptes de 360 graus) i al diàmetre li assigna 28 unitats. Això fa que la unitat d'angle sigui molt aproximadament el radian. La taula dona l'angle en graus, minuts i segons i és exacta fins a l'últim decimal.[4]
- El matemàtic indi Bhaskara II, l'any 1150 explica un mètode detallat per construir les taules de sinus per a qualsevol angle.[1]
- Madhava de Sangamagrama (1400) Va fer uns primers passos en l'anàlisi matemàtica de funcions trigonomètriques basada en sèries.
- Leonhard Euler amb l'obra Introductio in analysin infinitorum (1748) va ser el principal responsable d'establir el tractament de les funcions trigonomètriques a Europa, també les va definir com a sèries infinites i va presentar la fórmula d'Euler", així com les abreviatures gairebé igual que les modernes sin., cos., tang., cot., sec., i cosec.
Històricament era comú de fer servir unes quantes funcions més que les d'avui en dia (i aquestes funcions apareixen en les taules més antigues de funcions trigonomètriques), però en l'actualitat s'han deixat de fer servir. Són funcions com ara la corda (crd(θ) = 2 sin(θ/2)), el versinus (versin(θ) = 1 − cos(θ) = 2 sin²(θ/2)), el semiversinus (semiversin(θ) = versin(θ) / 2 = sin²(θ/2)), l'exsecant (exsec(θ) = sec(θ) − 1) i l'excosecant (excsc(θ) = exsec(π/2 − θ) = csc(θ) − 1). Moltes més relacions, entre les quals es troben aquestes, es troben a l'article sobre la llista d'identitats trigonomètriques.
Etimologia[modifica]
L'etimologia de la paraula sinus prové de la paraula en sànscrit jya-ardha que vol dir "mitja corda", abreujat en jiva. Això es transliterava en àrab com jiba, i s'escrivia jb, en no escriure les vocals en àrab. Després, aquesta transliteració va ser traduïda per error al segle xii al llatí com a sinus, sota la impressió equivocada que jb corresponia a la paraula jaib, que significa "pit" o "badia" o "plec" en àrab, tal com sinus en llatí.[5] La paraula llatina és la que s'ha conservat en català.
La paraula tangent ve del llatí tangens: que "toca", ja que la recta emprada per definir-la toca la circumferència goniomètrica, mentre que secant prové de secans en llatí - "tallant" - ja que la recta emprada per definir-la talla la circumferència goniomètrica: ambdues van ser introduïdes pel matemàtic danès Thomas Fincke el 1583.[6]
Definició de les funcions trigonomètriques[modifica]
Les diferents definicions de les funcions trigonomètriques que es presenten a continuació són equivalents en el sentit que, per als angles en què es poden aplicar, el resultat coincideix. Però es diferencien en el sentit que es poden aplicar a angles en un sentit cada cop més ampli de la paraula. La definició basant-se en el triangle rectangle, estrictament parlant, només es pot aplicar a angles aguts. La definició basant-se en la circumferència goniomètrica permet atribuir valor a les funcions trigonomètriques d'angles que tinguin qualsevol valor dins del conjunt dels nombres reals. La definició basada en sèries es pot fer servir per calcular les funcions trigonomètriques d'arguments complexos.
A més, les definicions basades en sèries, en equacions diferencials o en equacions funcionals, permeten abordar l'estudi de les funcions trigonomètriques sense fer referència a consideracions geomètriques. Simplement acceptant la definició basada purament en conceptes propis de l'anàlisi matemàtica.
Basant-se en el triangle rectangle[modifica]
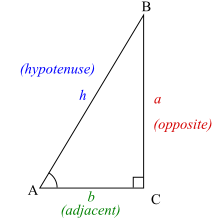
Per tal de definir les funcions trigonomètriques de l'angle A, es comença amb un triangle rectangle arbitrari que contingui l'angle A. Es fan servir els següents noms pels costats del triangle:
- La hipotenusa és el costat oposat a l'angle recte, o també es pot definir com el costat més llarg del triangle rectangle, en aquest cas h.
- El catet oposat és el costat oposat a l'angle que es pretén estudiar, en aquest cas a.
- El catet adjacent és el costat que està en contacte amb l'angle que s'està estudiant i l'angle recte. En aquest cas el catet adjacent és b.
Tots els triangles es prenen en el pla euclidià; d'aquesta forma els angles interns de qualsevol triangle sumen π radiants (o 180°). Per tant, per a qualsevol triangle rectangle els angles no rectes són entre zero i π/2 radiants (o 90°). Cal observar que les següents definicions, parlant estrictament, només defineixen les funcions trigonomètriques per angles dins d'aquest interval. S'estenen al conjunt sencer dels arguments reals a base de fer servir la circumferència goniomètrica, o a base d'imposar certes simetries i que siguin funcions periòdiques.
En la següent taula es recullen les definicions de les sis funcions trigonomètriques sobre la base del triangle rectangle:[7]
| Nom | Definició | Fórmula | Triangle de la figura |
|---|---|---|---|
| Sinus | El sinus d'un angle és el quocient entre la longitud del catet oposat i la longitud de la hipotenusa. | ||
| Cosinus | El cosinus d'un angle és el quocient entre la longitud del catet adjacent i la hipotenusa. | ||
| Tangent | La tangent d'un angle és el quocient entre la longitud del catet oposat i la longitud del catet adjacent. | ||
| Cosecant | La cosecant és la inversa del sinus, és a dir, el quocient entre la longitud de la hipotenusa i la longitud del catet oposat. | ||
| Secant | La secant és la inversa del cosinus, és a dir, el quocient entre la longitud de la hipotenusa i la longitud del catet adjacent. | ||
| Cotangent | La cotangent és la inversa de la tangent, és a dir, el quocient entre la longitud del catet adjacent i la longitud del catet oposat. |
Es pot veure que aquests quocients no depenen del triangle rectangle concret que s'hagi escollit, atès que tots els triangles rectangles que tinguin l'angle A són semblants.
Basant-se en la circumferència goniomètrica[modifica]


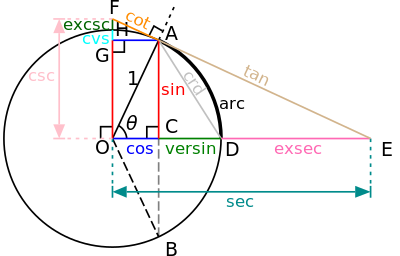
Les sis funcions trigonomètriques també es poden definir en base la circumferència goniomètrica, la circumferència de radi unitat el centre de la qual és l'origen d'un sistema de coordenades cartesianes. La circumferència goniomètrica aporta poc en el camí cap als càlculs pràctics, si no que es recolza en els triangles rectangles per a la majoria d'angles. En canvi, la definició basada en la circumferència goniomètrica, permet la definició de les funcions trigonomètriques per a tots els arguments reals, tant positius com negatius, no només per a angles entre 0 i π/2 radiants. També dona una imatge visual única que conté de cop tots els angles rellevants. A partir del Teorema de Pitàgores l'equació de la circumferència de radi unitat centrada a l'origen és:
Observant la figura de la dreta. Sia una segment de línia recta que va de l'origen fins a la circumferència goniomètrica i forma un angle positiu t amb la meitat positiva de l'eix x. Les coordenades x i y de l'extrem d'aquest segment que toca la circumferència goniomètrica són, respectivament, el cos t i el sin t.[8] Traçant una perpendicular a l'eix x que passi per l'extrem del segment s'obté un triangle rectangle format pel segment, aquesta perpendicular i l'eix x. Aquest triangle rectangle permet comprovar que pels angles del primer quadrant la definició coincideix amb la definició basada en el triangle rectangle. Com que el radi del cercle és igual a la hipotenusa i té longitud 1, resulta que sin θ = y/1 i cos θ = x/1. La circumferència goniomètrica, es pot entendre com una forma de representar un nombre infinit de triangles rectangles, en els que varien les longituds dels catets, però que la longitud de la hipotenusa es conserva constant igual a 1.

Per angles més grans que π/2 i més petits que π la coordenada x del punt passa a ser negativa i la coordenada y és la mateixa que la del triangle obtingut per simetria especular respecte de l'eix vertical, per tant per a aquests angles la definició basant-se en la circumferència goniomètrica és el mateix que estendre la definició a partir del triangle rectangle imposant les següents identitats:
Seguint el mateix raonament amb simetries respecte de l'eix horitzontal resulta que entre π i 3π/2 el sinus també esdevé negatiu i la definició basant-se en la circumferència goniomètrica és equivalent a estendre la definició a partir del triangle rectangle amb les següents imposicions:
I al tercer quadrant (és a dir entre 3π/2 i 2π):
A la figura de la dreta es presenten els valors del sinus i el cosinus dels angles més habituals en els quatre quadrants.
Per angles més grans que 2π o més petits que −2π, senzillament es continua girant al voltant del cercle. D'aquesta forma, el sinus i el cosinus esdevenen funcions periòdiques amb període 2π:
Per a qualsevol angle θ i qualsevol enter k.
Del període positiu més petit d'una funció periòdica se'n diu el període fonamental de la funció.[9] El període fonamental del sinus, el cosinus, la secant, i la cosecant, és el cercle complet, és a dir, 2π radiants o 360 graus; el període fonamental de la tangent i la cotangent és només la meitat del cercle, és a dir π radiants o 180 graus. Més amunt, només s'han definit, a través de la circumferència goniomètrica, el sinus i el cosinus, però les altres quatre funcions trigonomètriques es poden definir per:
A la figura de la dreta es presenten les gràfiques de les funcions trigonomètriques esteses al llarg dels nombres reals.
De forma alternativa, totes les funcions trigonomètriques bàsiques es poden definir en termes de la circumferència goniomètrica (que es presenta a la dreta al començament de la pàgina), i definicions geomètriques d'aquest estil són les que es varen fer servir històricament i són les que justifiquen el nom de les funcions. En particular, la corda AB del cercle, on θ és la meitat de l'angle, sin(θ) és AC (la meitat de la corda), una definició que va ser introduïda a l'Índia (vegeu més amunt la història de les funcions trigonomètriques). cos(θ) és la distància horitzontal OC, i el versin (θ) = 1 − cos(θ) és CD. tan(θ) és la longitud del segment AE de la línia tangent a la circumferència goniomètrica al punt A, d'aquí la paraula tangent per aquesta funció. cot(θ) és un altre segment tangent, AF. sec(θ) = OE i csc(θ) = OF són segments de línies secants (que intersequen el cercle a dos punts), i també es poden veure com projeccions de OA al llarg de la tangent a A sobre els eixos horitzontal i vertical respectivament. DE és la exsec (θ) = sec(θ) − 1 (la porció de la secant fora de, o ex, el cercle). A partir d'aquestes construccions, és fàcil de veure que les funcions secant i tangent divergeixen a mesura que θ tendeix a π/2 (90 graus) i que la cosecant i la cotangent divergeixen a mesura que θ tendeix a zero. (Hi ha moltes construccions semblants possibles, i les identitats trigonomètriques bàsiques, també es poden demostrar gràficament.)
Basant-se en sèries[modifica]

Fent servir només geometria i les propietats dels límits, es pot demostrar que, la derivada del sinus és el cosinus i la derivada del cosinus és menys el sinus (sempre que els angles es mesurin en radiants, vegeu derivació de les funcions trigonomètriques). Llavors es pot fer servir la teoria de les sèries de Taylor per demostrar que les següents identitats es donen per a tots els nombres reals x:[10]
Aquestes identitats sovint s'agafen com a definicions de les funcions sinus i cosinus.[11] Sovint es fan servir com un punt de partida per a un tractament rigorós de les funcions trigonomètriques i les seves aplicacions (per exemple, en les sèries de Fourier), atès que la teoria de les sèries es pot desenvolupar a partir dels fonaments dels nombres reals, de forma independent de qualsevol mena de consideracions geomètriques. Llavors, la derivabilitat i la continuïtat d'aquestes funcions s'estableixen només a partir de les definicions de les sèries.
A partir d'un teorema d'anàlisi complexa, hi ha una única extensió analítica d'aquestes funcions reals al conjunt dels nombres complexos. Aquestes extensions tenen les mateixes sèries de Taylor, d'aquesta forma, les funcions trigonomètriques es defineixen en el conjunt dels nombres complexos emprant les sèries de Taylor de més amunt.
En les següents gràfiques, el domini és el pla complex. Per representar el nombre complex imatge de cada punt es fa servir el color per indicar l'argument, i la lluentor per indicar el mòdul. El color negre correspon al zero. Vegeu (conveni de colors)
 |
 |
 |
 |
 |
 |
També es poden trobar altres sèries:[12]
on
- és el n-èsim nombre de la transformada de Boustrophedon,
- és el n-èsim nombre de Bernoulli, i
- (davall) és l'n-èsim nombre d'Euler.
Quan això s'expressa de forma que els denominadors són els corresponents factorials i el numeradors, anomenats els "nombres tangents" tenen una interpretació combinatòria: enumeren permutacions alternades de conjunts finits de cardinalitat senar.
Quant això s'expressa en una forma en què els denominadors són els corresponents factorials, els numeradors, anomenats els "nombres secants", tenen una interpretació combinatòria: enumeren les permutacions alternades de conjunts de cardinalitat parell.
Emprant equacions diferencials[modifica]
Tant la funció sinus com la funció cosinus satisfan l'equació diferencial
- .
És a dir, cada una és el negatiu de la seva pròpia derivada segona. En l'espai funcional de dues dimensions V consistent en totes les solucions d'aquesta equació, la funció sinus és l'única solució que satisfà les condicions inicials y(0) = 0 i y′(0) = 1, i la funció cosinus és l'única solució que satisfà les condicions inicials y(0) = 1 i y′(0) = 0. Atès que les funcions sinus i cosinus són linealment independents, juntes formen una base de V. Aquest mètode de definir les funcions sinus i cosinus, és essencialment equivalent a fer servir la fórmula d'Euler. (Vegeu: Equació diferencial lineal.) Resulta que aquesta equació diferencial no només es pot fer servir per a definir les funcions sinus i cosinus, sinó que també es pot fer servir per a demostrar les identitats trigonomètriques de les funcions sinus i cosinus. A més, l'observació que les funcions sinus i cosinus satisfan significa que són les funcions pròpies de l'operador derivada segona.
La funció tangent és l'única solució de l'equació diferencial no lineal
que satisfà la condició inicial y(0) = 0. Hi ha una demostració visual molt interessant que la funció tangent satisfà aquesta equació diferencial; vegeu Needham's Visual Complex Analysis.[13]
Conseqüències de fer servir radiants[modifica]
Els radiants especifiquen un angle a base de mesurar la longitud de l'arc sobre el cercle de radi unitat i constitueixen un argument especial per a les funcions sinus i cosinus. En particular, només aquestes sinus i cosinus que apliquen radiants a quocients satisfan les equacions diferencials que els descriuen de forma clàssica. Si a l'argument del sinus o del cosinus en radiants se li aplica un factor d'escala (es multiplica per una freqüència),
Llavors les derivades resulten multiplicades per una factor d'escala en l'amplitud.
- .
Aquí, k és una constant que representa un factor de canvi d'unitats. Si x està en graus, llavors
- .
Això significa que la derivada segona del sinus en graus no satisfà l'equació diferencial
- ,
sinó
- ;
la derivada segona del cosinus es comporta de forma similar.
Això significa que aquests sinus i cosinus (mesurant els angles en una unitat diferent del radiant) són funcions diferents, i que les derivades quartes del sinus, només tornaran a ser altre cop sinus si l'argument ve donat en radiants.
Emprant equacions funcionals[modifica]
En anàlisi matemàtica, les funcions trigonomètriques es poden definir emprant equacions funcionals basades en propietats com les fórmules de la suma i la diferència. Prenent com a dades aquestes fórmules i la identitat de Pitàgores, per exemple, es pot demostrar que només hi ha dues funcions reals que satisfan aquestes condicions. Simbòlicament es pot dir que existeix exactament un parell de funcions reals sin i cos tals que per a qualsevulla nombres reals x i y, es compleixen les següents equacions:
amb la condició afegida que
- .
També són possibles altres deduccions començant a partir d'altres equacions funcionals i aquestes definicions es poden estendre als nombres complexos. Com a exemple, aquest camí es pot fer servir per definir la trigonometria en cossos de Galois.
Relació de les funcions trigonomètriques amb la funció exponencial i els nombres complexos[modifica]

A partir del desenvolupament en sèrie de la funció exponencial:
Es calcula l'exponencial d'iθ:
Tot seguit s'agrupen els termes parells i els senars (la reordenació dels termes es pot fer a causa del fet que la sèrie és uniformement convergent) i es treu factor comú i:
Observant el desenvolupament en sèrie de les funcions sinus i cosinus queda clar que això és igual a:
D'aquesta identitat se'n diu la fórmula d'Euler. D'aquesta forma les funcions trigonomètriques esdevenen essencials en la interpretació geomètrica de l'anàlisi complexa. Per exemple, amb la identitat de dalt, si es considera el cercle unitat en el pla complex, definit per eix, i tal com s'ha fet abans, es pot parametritzar aquest cercle en termes de cosinus i sinus, la relació entre l'exponencial complexa i les funcions trigonomètriques esdevé més clara.
A més, això permet la definició de les funcions trigonomètriques per arguments complexos z:
on i² = −1. També, per x reals purs,
També és conegut que els processos exponencials estan íntimament lligats al comportament periòdic.
Identitats trigonomètriques[modifica]
Hi ha moltes identitats matemàtiques relacionades amb les funcions trigonomètriques. Entre les més utilitzades hi ha la identitat de Pitàgores, que estableix que per qualsevol angle, el sinus al quadrat més el cosinus al quadrat dona 1. És fàcil de veure, considerant el triangle rectangle amb la hipotenusa de longitud 1 i aplicant el teorema de Pitàgores. La identitat de Pitàgores s'escriu,
- ,
O més freqüentment escrivint l'exponent "dos" al costat dels símbols sinus i cosinus:
- .
En alguns casos els parèntesis interiors es poden ometre.
Aquesta identitat permet expressar el sinus en funció del cosinus o viceversa, conjuntament amb les identitats que sorgeixen de les definicions de les funcions trigonomètriques permet expressar qualsevol de les sis funcions trigonomètriques en funció de qualsevol de les altres (pel cas d'angles aguts sense cap mena d'ambigüitats, pels altres cal informació addicional per determinar el signe de les funcions). A la següent taula es resumeixen aquestes identitats:
| Funció | sin | cos | tan | csc | sec | cot |
|---|---|---|---|---|---|---|
Altres relacions importants són les fórmules de les funcions trigonomètriques de la suma i la diferència d'angles, que donen el sinus i el cosinus de la suma o la diferència de dos angles en funció del sinus i del cosinus dels propis angles. Es poden obtenir per raonaments geomètrics, emprant arguments que es retrotreuen a l'època de Claudi Ptolemeu. Aquestes fórmules són especialment importants perquè a partir d'elles es troba la derivada de les funcions trigonomètriques que és necessària per demostrar la fórmula d'Euler. Un cop coneguda la fórmula d'Euler es pot emprar per memoritzar aquestes identitats a base de deduir-les ràpidament:
Com que, perquè dos nombres complexos siguin iguals, han de ser iguals les seves parts reals i les seves parts imaginàries, resulten directament les identitats que es buscaven. Pel cas de la diferència només cal aplicar les mateixes fórmules i tenir en compte les simetries de les funcions sinus i cosinus en aplicar-les a angles negatius, el resultat són les quatre identitats:
Per a una demostració basada en raonaments geomètrics vegeu: Demostració de les identitats de la suma d'angles.
Quan els dos angles són iguals, les fórmules de la suma es redueixen a identitats més senzilles conegudes amb el nom de fórmules de l'angle doble, o aplicant-les repetidament les de l'angle triple. A partir de les fórmules de l'angle doble es troben les fórmules d'angle meitat.
| Fórmules de l'angle doble[14] | |||
|---|---|---|---|
| Fórmules de l'angle triple[15] | |||
| Fórmules de l'angle meitat[16] | |||
Aquestes identitats es poden fer servir per demostrar fórmules de Simpson que permeten passar de productes a sumes i de sumes a productes. Antigament es feien servir en comptes dels logaritmes per a transformar el producte de dos nombres en una suma i augmentar la velocitat dels càlculs.
Identitats trigonomètriques en càlcul infinitesimal[modifica]
Per a les identitats que sorgeixen en derivar i integrar les funcions trigonomètriques, vegeu: Derivació de les funcions trigonomètriques, taula d'integrals de funcions trigonomètriques, Llista d'integrals de funcions trigonomètriques i Llista d'integrals d'inverses de funcions trigonomètriques.
Càlcul de les funcions trigonomètriques[modifica]
El càlcul de les funcions trigonomètriques és una qüestió complicada que avui en dia pot ser evitada per la majoria de la gent a causa de l'ampla disponibilitat dels ordinadors i de les calculadores científiques que ofereixen càlcul preprogramat de funcions trigonomètriques per a qualsevol angle. Ara bé, en aquesta secció es donen més detalls sobre el seu càlcul en tres contexts importants: l'ús històric de les taules trigonomètriques, les tècniques modernes que es fan servir per programar els ordinadors per a calcular-les, i en quant angles "importants" per als quals els valors exactes simplement es poden trobar de forma senzilla.
En tot el que segueix, n'hi ha prou de considerar un recorregut petit d'angles, de 0 a π/2, atès que els altres angles es poden reduir a aquests gràcies a les simetries i a la periodicitat de les funcions trigonomètriques.
Abans de l'aparició dels ordinadors, la gent avaluava les funcions trigonomètriques per interpolació a partir de les taules amb els valors calculats amb molts dígits significatius. Aquestes taules han estat construïdes des de tant antic com la descripció de les mateixes funcions trigonomètriques (vegeu història de les funcions trigonomètriques). Normalment es generaven a base d'aplicar repetidament les fórmules de l'angle meitat i de la suma d'angles començant a partir d'un valor conegut, tal com per exemple sin(π/6)=1/2.
Els ordinadors moderns fan servir una gran varietat de tècniques.[17] Un mètode habitual, especialment en processadors amb unitats de coma flotant, és combinar una aproximació per un polinomi o una funció racional (com ara l'aproximació de Chebyshev, l'aproximació uniforme òptima, i l'aproximació de Padé, i per a precisions més altes o precisions variables, la sèrie de Taylor i la sèrie de Laurent) amb una reducció del recorregut i una cerca en taula — primer busquen en una petita taula l'angle més proper, i llavors utilitzen el polinomi per a calcular la correcció.[18] En dispositius més senzills als que els manquen unitats de maquinari per a fer multiplicacions, hi ha un algorisme anomenat CORDIC (amb les seves tècniques relacionades) que és més eficient perquè només fa servir sumes i l'operació desplaçament. Tots aquest mètodes es poden implementar en circuits especialitzats per motius d'eficiència.
Per a càlculs de molt alta precisió, quan la convergència de les sèries esdevé massa lenta, les funcions trigonomètriques es poden aproximar amb la mitjana aritmètico-geomètrica, que ella mateixa aproxima la funció trigonomètrica per la integral el·líptica (complexa).[19]
Finalment, per alguns angles senzills, els valors es poden calcular fàcilment a mà emprant el teorema de Pitàgores, com en els exemples que es presentaran a continuació. De fet, el sinus, el cosinus i la tangent de qualsevol múltiple enter de radiants (3°) es pot calcular exactament a mà.
Es considera el triangle rectangle que té iguals els altres dos angles diferents del recte, per tant tots dos valen radiants (45°). Llavors la longitud dels costats b i a són iguals; es pot definir . Els valors del sinus, del cosinus i de la tangent de radiants (45°) llavors es poden trobar emprant el teorema de Pitàgores:
- .
Per tant:
- ,
- .
Per a determinar les funcions trigonomètriques dels angles de π/3 radiants (60 graus) i π/6 radiants (30 graus), es comença amb una triangle equilàter de longitud 1 de costat. Tots els seus angles són de π/3 radiants (60 graus). Partint-lo per la meitat, s'obté un triangle rectangle amb angles de π/6 radiants (30 graus) i π/3 radiants (60 graus). Per aquest triangle, el costat més petit té una longitud de 1/2, el costat següent té una longitud de (√3)/2 i la hipotenusa 1. Això dona:
- ,
- ,
- .
A la següent taula es resumeixen aquests resultats:
| Funció | 0°
|
30°
|
45°
|
60°
|
90°
|
|---|---|---|---|---|---|
| Sinus | |||||
| Cosinus | |||||
| Tangent |
Les expressions s'han posat sense simplificar perquè així és més fàcil memoritzar-les.
Funcions inverses[modifica]
Les funcions trigonomètriques són periòdiques, i per tant no injectives, així, estrictament parlant, no tenen funció inversa. Per a definir una funció inversa cal restringir el domini de forma que les funcions trigonomètriques siguin bijectives. En el que segueix, les funcions de l'esquerra són definides per l'equació de la dreta; no són identitats demostrades. Les inverses principals, es defineixen normalment com:
Per a les inverses de les funcions trigonomètriques, sovint es fan servir les notacions sin−1 i cos−1en comptes d'arcsin i arccos, etc. Quan es fa servir aquesta notació, les inverses de les funcions es podrien confondre amb les inverses del valor de les funcions respecte de la multiplicació. La notació emprant el prefix "arc-" evita aquesta confusió.
De la mateixa manera que el sinus i el cosinus, les inverses de les funcions trigonomètriques també es poden definir en termes de sèries infinites. Per exemple,
Aquestes funcions també es poden definir com les primitives d'altres funcions. Per exemple, l'arcsinus, es pot escriure com la següent integral:
Es poden trobar fórmules anàlogues a aquestes a l'article Inverses de les funcions trigonomètriques.
Emprant el logaritme complex, es poden generalitzar totes aquestes funcions a arguments complexos:
Propietats i aplicacions[modifica]

Les funcions trigonomètriques, tal com suggereix el seu nom, són d'importància crucial en trigonometria i en la resolució de triangles, principalment a causa de l'aplicació del teorema del sinus, el del cosinus i el de la tangent.
La resolució de triangles és la tècnica en la que es basa la triangulació. Aplicant sistemàticament aquesta tècnica es va fer la triangulació dels Països Catalans que es reprodueix a la figura de la dreta. La part que va des de Salses fins a Barcelona la va fer el científic francès Pierre Méchain i la part que va des de Barcelona fins a Mallorca la va començar Méchain juntament amb el científic català Francesc Aragó i la va acabar aquest últim en morir Méchain a Castelló de la Plana sense haver pogut acabar els treballs. Aquesta part juntament amb la part francesa va servir per mesurar el meridià de París i aquesta mesura es la que es va fer servir per definir el metre patró.[20]
Teorema del sinus[modifica]
El teorema del sinus estableix que per a qualsevol triangle de costats a, b, i c i angles oposats a aquests costats A, B i C:
també conegut com:
on R és el radi de la circumferència circumscrita.

Es pot demostrar a base de dividir el triangle en dos triangles rectangles i fent servir la definició del sinus. El teorema del sinus és útil per a calcular les longituds dels costats desconeguts d'un triangle si es coneixen dos angles i un constat. Aquesta és una situació que succeeix normalment en triangulació, una tècnica per a determinar distàncies desconegudes a base de mesurar dos angles i una distància accessible entre els dos angles.
Teorema del cosinus[modifica]
El teorema del cosinus és una extensió del teorema de Pitàgores:
També conegut com:
En aquesta fórmula l'angle C és oposat al costat c. Aquest teorema es pot demostrar dividint el triangle en dos triangles rectangles i emprant el teorema de Pitàgores.
El teorema del cosinus es fa servir principalment per determinar un costat d'un triangle si es coneixen els altres dos costats i un dels angles, tot i que de vegades hi pot haver dues solucions positives. També es pot fer servir per a trobar el cosinus d'un angle (i en conseqüència l'angle mateix) si es coneixen tots tres costats.
Teorema de la tangent[modifica]
El teorema de la tangent estableix que:
Funcions periòdiques[modifica]

En física les funcions sinus i cosinus, per exemple, es fan servir per a descriure el moviment harmònic simple, el qual és un model de fenòmens naturals, com ara el moviment d'una massa fixada en una molla i, per angles petits, el moviment pendular d'una massa penjada d'una corda. Les funcions sinus i cosinus són les projeccions unidimensionals del moviment circular uniforme.[21]
Les funcions trigonomètriques també han demostrat ser útils en l'estudi de les funcions periòdiques en general. Aquestes funcions tenen gràfiques i ones característiquess, útils per a modelitzar fenòmens recurrents com ara les ones de llum o sonores. Cada senyal es pot escriure com un sumatori (normalment infinit) de funcions sinus i cosinus de diferents freqüències; aquesta és la idea en què es basa l'anàlisi de Fourier, on les funcions trigonomètriques es fan servir per a resoldre una gran varietat de problemes de condicions de contorn en equacions diferencials amb derivades parcials. Per exemple, l'ona quadrada:
es pot escriure com una sèrie de Fourier.[22]
- .
A l'animació de la dreta es pot veure que amb només una quants termes s'aconsegueix una aproximació força bona.
Vegeu també[modifica]
- Construcció de les taules trigonomètriques
- Funcions hiperbòliques
- Teorema de Pitàgores
- Llista d'identitats trigonomètriques
- Demostració de les identitats trigonomètriques
- Fórmula d'Euler
Notes[modifica]
- ↑ 1,0 1,1 1,2 O'Connor (1996).
- ↑ Boyer, pàg. 158–168.
- ↑ Abūʾl-Wafā Article sobre Abūʾl-Wafā a l'Enciclopèdia Britànica.
- ↑ Llibre de Geometria[Enllaç no actiu], Abraham Bar Hiia (Savasorda), Biblioteca Hebraico-Catalana, ISBN 978-84-9859-106-4 pàgina 82
- ↑ Vegeu Maor (1998), capítol 3, referent a etimologia.
- ↑ Sozio, Gerardo «Trigonometry: Chords, Arcs and Angles» (en (anglès)). Parabola. University of New South Wales [Sidney (Austràlia)], Vol. 41, Num. 1, 2005, pàg. 10.
- ↑ Iniciació a les matemàtiques per a l'enginyeria Arxivat 2016-03-13 a Wayback Machine. Pàgina de la UOC on es defineixen les funcions trigonomètriques basant-se en el triangle rectangle]
- ↑ Càlculus A la pàgina 437 hi ha la definició del sinus i el cosinus basant-se en la circumferència goniomètrica.
- ↑ Senyals Periòdics. Portal d'Aprenentatge Obert de l'Escola d'Enginyeria de Telecomunicació, Tutorial: Els senyals, Núria Garcia Garcia, Processament del senyal, Característiques bàsiques dels senyals
- ↑ Vegeu Lars Ahlfors, pàgines 43–44.
- ↑ Definició de les funcions trigonomètriques basant-se en sèries
- ↑ Abramowitz; Weisstein.
- ↑ Needham, pàg. ix.
- ↑ Weisstein, Eric W., «Double-Angle Formulas» a MathWorld (en anglès).
- ↑ Weisstein, Eric W., «Multiple-Angle Formulas» a MathWorld (en anglès).
- ↑ Weisstein, Eric W., «Half-Angle Formulas» a MathWorld (en anglès).
- ↑ Kantabutra.
- ↑ Ara bé, fer això i mantenir la precisió no és trivial, i es poden fer servir mètodes com les taules de precisió de Gal, la reducció de Cody i Waite, i els algorismes de reducció de Payne i Hanek.
- ↑ R. P. Brent, "Fast Multiple-Precision Evaluation of Elementary Functions", J. ACM 23, 242 (1976).
- ↑ Un passeig per la història del sistema mètric decimal, Anton Aubanell Pou, Càtedra "Lluís Santaló" de la Universitat de Girona.
- ↑ http://cns.upf.edu/laura/teaching/ffi/teoria_osc.pdf Arxivat 2009-09-20 a Wayback Machine. Fonaments Físics de la Informàtica] Capítol 2 oscil·lacions
- ↑ Notes sobre sèries i transformada de Fourier Arxivat 2010-04-02 a Wayback Machine., Catalina Sbert, 2005, pègina 2
Referències[modifica]
- Lars Ahlfors. Complex Analysis: an introduction to the theory of analytic functions of one complex variable, segona edició, McGraw-Hill Book Company, Nova York, 1966.
- Abramowitz, Milton; Irene A. Stegun. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover, Nova York. (1964). ISBN 0-486-61272-4.
- Boyer, Carl B.. A History of Mathematics, John Wiley & Sons, Inc., segona edició. (1991). ISBN 0-471-54397-7.
- Joseph, George G. The Crest of the Peacock: Non-European Roots of Mathematics, segona edició Penguin Books, Londres. (2000). ISBN 0-691-00659-8.
- Kantabutra, Vitit. "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328–339 (1996).
- Maor, Eli. Trigonometric Delights Arxivat 2006-04-14 a Wayback Machine., Princeton Univ. Press. (1998). Reimpressió (25 febrer de 2002): ISBN 0-691-09541-8.
- Needham, Tristan. "Preface" Arxivat 2004-06-02 a Wayback Machine." a Visual Complex Analysis Arxivat 2008-06-07 a Wayback Machine.. Oxford University Press, (1999). ISBN 0-19-853446-9.
- O'Connor, J.J.; E.F. Robertson. "Trigonometric functions" Arxivat 2013-01-20 a Wayback Machine., Arxiu d'història de les matemàtiques a MacTutor. (1996).
- O'Connor, J.J.; E.F. Robertson. "Madhava of Sangamagramma", Arxiu d'història de les matemàtiques a MacTutor. (2000).
- Pearce, Ian G. "Madhava of Sangamagramma" Arxivat 2006-05-05 a Wayback Machine.. Arxiu d'història de les matemàtiques a MacTutor. (2002).
- Weisstein, Eric W. "Tangent" a MathWorld, accés el 21 de gener de 2006.
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Funció trigonomètrica |



















































































































![{\displaystyle {\begin{aligned}&\cos \left(x+y\right)+i\sin \left(x+y\right)=e^{i\left(x+y\right)}=e^{ix}e^{iy}\\&e^{ix}e^{iy}=\left[\cos \left(x\right)+i\sin \left(x\right)\right]\cdot \left[\cos \left(y\right)+i\sin \left(y\right)\right]=\\&=\left[\cos \left(x\right)\cos \left(y\right)-\sin \left(x\right)\sin \left(y\right)\right]+i\left[\cos \left(x\right)\sin \left(y\right)+\sin \left(x\right)\cos \left(y\right)\right]\\&\cos \left(x+y\right)=\cos \left(x\right)\cos \left(y\right)-\sin \left(x\right)\sin \left(y\right)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8f658c68ac51dbda835a579f87fec6564e1705c)
















































![{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan[{\frac {1}{2}}(A+B)]}{\tan[{\frac {1}{2}}(A-B)]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc3a9eabede6ceceb176a58754cf6557b46f7c3c)


