Trigonometria esfèrica

Triangle esfèric trirectangle ( els seus angles sumen ' : 270°).

La trigonometria esfèrica és un conjunt de relacions anàlogues a les de la trigonometria plana, però en aquest cas, amb angles i distàncies disposades sobre una esfera. Les regles habituals de la trigonometria plana ja no seran vàlides; per exemple la suma dels angles d'un triangle situat sobre una esfera és superior a $\pi \,$ i els segments de rectes es transformen en arcs de cercles màxims. La paraula deriva del grecτρίγωνον trigōnon, "triangle" i μέτρον metron, "mesurar" .

Context històric

Hi ha evidència que fins i tot els babilonis i els egipcis es van preocupar pels problemes de trigonometria esfèrica fa 4.000 anys per poder calcular la trajectòria de les estrelles, no obstant això, no podien resoldre'ls. De fet, la història de la trigonometria esfèrica està tant estretament relacionada amb l'astronomia, que en el moment en què els grecs van començar a emprar-la per als seus càlculs, aproximadament el 350 aC, es va convertir en la ciència base per ajudar els astrònoms a predir els moviments dels astres.

El text més antic sobre trigonometria esfèrica data d'aquest període, va ser el grec Autolykos de Pitane i conté frases sobre cercles esferoidals. Al voltant del 140 aC. Hipparc de Nicea, va fer estudis sobre mètodes, tant computacionals com gràfics, per crear diagrames estel·lars i realitzar nous càlculs astronòmics. Menelau d'Alexandria, el 98 aC.va transferir les primeres fórmules del triangle pla als triangles sobre l'esfera i va trobar que el valor de la suma dels angles d'un triangle esfèric era 270°.

Entre el 125 i el 150 dC, Ptolemeu d'Alexandria va trobar els mètodes per a calcular triangles esfèrics tant rectangles com oblics. Des de l'Índia, van arribar les primeres aproximacions a la fórmula del cosinus. Entre els matemàtics àrabs que, basant-se en la recerca feta pels indis i grecs van continuar els estudis sobre la trigonometria esfèrica, val la pena esmentar Al-Battaní (al voltant de 900 n. Chr.) I Nasir Eddin Tusi (al voltant de 1250 n. Chr.), que va plasmar per primera vegada el teorema del sinus i el triangle polar en fórmules matemàtiques. Al segle xv, Johannes Müller regiomontanus va ampliar el coneixement grec, indi i àrab amb la funció tangent les investigacions en trigonometria esfèrica van facilitar els grans viatges de descobriment al poder determinar millor la posició d'un vaixell al mar, permetent traçar les noves rutes marítimes cap a l'Índia, Amèrica i el Pacífic.

Vieta es troba al segle xvi sobre el triangle polar Winkel kosinussatz. John Napier (Napier, 1550-1617) va portar les fórmules trigonomètriques a regles fàcilment aplicables (el Pentàgon de Neper). Finalment Leonhard Euler (1707-1783), va redactar la trigonometria esfèrica actual d'una forma clara.

Després d'Euler molts altres matemàtics han ampliat la trigonometria esfèrica, establint noves relacions entre els costats i els angles d'un triangle esfèric, entre altres: Simon L'Huilier (1750-1840), Jean-Baptiste Joseph Delambre (1749-1822), Carl Friedrich Gauss (1777-1855), Adrien-Marie Legendre (1752-1833) i David Hilbert (1862-1943). Gràcies al treball d'aquest matemàtics, que van descobrir nous mètodes, o en van aplicar d'antics, com els logaritmes de Napier, es va facilitar el desenvolupament de la geometria esfèrica en camps com per exemple, la topografia de la terra o la cartografia moderna. En els segles XIX i XX també es van descobrir altres geometries no euclidianes que junt amb la trigonometria esfèrica van trobar la seva aplicació en la teoria de la relativitat.

El triangle esfèric

Triangle esfèric

Si se situen dos punts sobre una superfície esfèrica, la corba més curta sobre aquesta superfície que els uneix és un dels dos arcs del cercle màxim que aquests dos punts determinen. Aquest cercle màxim queda perfectament determinat per dos punts diferents qualssevol sobre l'esfera. Cal recordar que tots els cercles màxims d'una esfera tenen el mateix radi que l'esfera.

Un triangle esfèric no queda totalment determinat per tres punts A, B i C situats sobre la superfície esfèrica. Ja que, per exemple en el cas de l'adjunta imatge, els tres punts A, B i C, a part del triangle a, b i c remarcat pel dibuix, també són els vèrtexs del triangle a, ${\bar {b}}$' i ${\bar {c}}$, entenent per ${\bar {b}}$ i ${\bar {c}}$, els arcs complementaris de b i c respectivament.

Així doncs, a, b i c són els costats del nostre triangle, però en trigonometria esfèrica, a, b i c no s'han de veure com a longituds, sinó com a angles. Així, quan s'escriu a s'ha de pensar en l'angle $\angle$BOC, on O és el centre de l'esfera. Igualment b serà l'angle $\angle$AOC i c serà $\angle$AOB. Evidentment, la longitud de a és Ra, aquesta segona a en radians.

Una altra de les característiques són els angles, ja que aquí no ens trobem sobre una superfície plana. Per exemple el valor de l'angle $\alpha$ del vèrtex A és el que tindria un angle sobre el pla de la tangent a l'esfera en A, limitat per la recta definida per aquest pla tangent i el pla determinat pel cercle màxim que passa per A i B, d'una banda, i la recta definida pel mateix pla tangent i el pla determinat pel cercle màxim que passa per A i C, d'altra banda. En els triangles esfèrics no degenerats, no es compleix que la suma dels seus angles és igual a $\pi \,$, com passa amb els triangles d'un pla. En aquest cas es pot escriure $\pi <\alpha +\beta +\gamma <5\pi \,$.

Així doncs, en un triangle esfèric, considerem els següents elements:

• El seu radi: R.

• Els seus vèrtexs: A, B i C.

• Els costats, que tal com s'ha dit són els angles: a=$\angle$BOC, b=$\angle$AOC i c=$\angle$AOB.

• I els angles: $\alpha$, del vèrtex A. $\beta$, del vèrtex B i $\gamma$, del vèrtex C.

Triangle esfèric

Triangle esfèric.

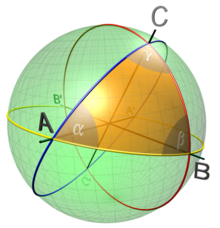
Si tres punts de la superfície esfèrica són units per arcs de cercle màxim menors a 180 º, la figura obtinguda s'anomena triangle esfèric. Els costats del polígon així format s'expressen per conveniència com a angle (essent el vèrtex el centre de l'esfera) i no per la seva longitud. Aquest arc mesurat en radians i multiplicat pel radi de l'esfera és la longitud de l'arc. En un triangle esfèric els angles compleixen que: P 180 ° <$\alpha \!$+$\beta \!$+$\gamma \!$ <540 °

Fórmules fonamentals

$\alpha \!$: angle format entre els arcs AC i AB.

$\beta \!$: angle format entre els arcs AB i BC.

$\gamma \!$: angle format entre els arcs AC i BC.

Fórmula del cosinus

$\cos CB=\cos AC\cos AB+{\rm {sin}}AC{\rm {sin}}AB\cos \alpha \!$

Fórmula del sinus

${\frac {{\rm {sin}}CB}{{\rm {sin}}\alpha }}={\frac {{\rm {sin}}AC}{{\rm {sin}}\beta }}={\frac {{\rm {sin}}AB}{{\rm {sin}}\gamma }}$

Els sinus dels costats són proporcionals als sinus dels angles oposats.

Fórmula de la cotangent

La fórmula de la cotangent també s'anomena fórmula dels elements consecutius. Veure en la figura dels següents elements consecutius:

angle $\alpha \!$; costat $AB$; angle $\beta \!$; costat $BC$.

$\cos \beta \cos AB={\rm {sin}}\beta \cot \alpha \!-{\rm {sin}}AB\cot CB$

cosinus dels elements mitjans, és igual a: si de l'angle mitjà per la cotangent de l'altre angle, menys si del costat mitjà per la cotangent de l'altre costat.

Fórmula de Bessel

Des de les fórmules dels cosinus, obtingudes en la secció anterior, es poden obtenir de immediat un conjunt de diverses fórmules conegudes com a "relacions del sinus pel cosinus" o també anomenades Fórmules de Bessel, o tercera fórmula de Bessel. Van ser deduïdes per primera vegada pel gran matemàtic Friedrich Wilhelm Bessel (Westfàlia, Alemanya, 1784 - Kaliningrad, Rússia, 1846):

cos a/k = cos b/k · cos c/k+sin b/k · sin c/k · cos A

cos b/k = cos c/k · cosa/k+sin c/k · sin a/k · cos B

cos c/k = cos a/k · cos b/k+sin a/k · sin b/k · cos C

El conjunt de les fórmules de Bessel es pot escriure, per a l'esfera de radi unitat, això és, l'esfera trigonomètrica de la forma:

$\sin {c}\cos {B}=\cos {b}\sin {a}-\cos {a}\sin {b}\cos {C}$

$\sin {c}\cos {A}=\cos {a}\sin {b}-\cos {b}\sin {a}\cos {C}$

$\sin {b}\cos {A}=\cos {a}\sin {c}-\cos {c}\sin {a}\cos {B}$

$\sin {b}\cos {C}=\cos {c}\sin {a}-\cos {a}\sin {c}\cos {B}$

$\sin {a}\cos {B}=\cos {b}\sin {c}-\cos {c}\sin {b}\cos {A}$

$\sin {a}\cos {C}=\cos {c}\sin {b}-\cos {b}\sin {c}\cos {A}$

Presentació matricial de les fórmules del triangle esfèric

El conjunt de les fórmules del sinus i del cosinus (anomenades per alguns segona i primera fórmila de Bessel), i la (tercera) fórmula de Bessel, poden expressar-se de forma matricial:

${\begin{vmatrix}cos(a)\\sin(a)sin(B)\\sin(a)cos(B)\end{vmatrix}}={\begin{vmatrix}cos(c)&0&sin(c)\\0&1&0\\sin(c)&0&-cos(c)\end{vmatrix}}.{\begin{vmatrix}cos(b)\\sin(b)sin(A)\\sin(b)cos(A)\end{vmatrix}}$

[Sent a, b, ic els costats i A, B, i C els vèrtexs del triangle esfèric]

Triangle esfèric rectangle

En triangle esfèric amb almenys un angle recte, se l'anomena triangle rectangle. En un triangle esfèric seus tres angles poden ser rectes, en aquest cas la suma és 270 °. En tots els altres casos aquesta suma excedeix els 180 ° ja aquest excés se l'anomena excés esfèric; s'expressa per la fórmula: E: E = $\alpha \!$+$\beta \!$+$\gamma \!$ - 180 °.

Qualsevol triangle esfèric pot descompondre's en dos triangles esfèrics rectangles.

Pentàgon de Neper

Pentàgon de Neper.

El pentàgon de Neper és una regla mnemotècnica per resoldre triangles esfèrics rectangles; pren aquest nom en memòria del científic anglès John Napier, i es construeix de la següent manera:

Es col·loquen en cada sector circular: catet - angle - catet - angle - catet, consecutivament, tal com apareixen ordenats en el triangle, exceptuant l'angle recte C .

Es reemplacen els angles B , C , i la hipotenusa a pels seus complementaris:

: B per (90 ° - B) : C per (90 ° - C) : A per (90 ° - a)

S'estableixen dues regles:

• El sinus d'un element és igual al producte de les tangents dels elements adjacents:

: Si (a) = tg (b) tg (90 ° - B), o el seu equivalent: si (a) = tg (b) CTG (B)

• El sinus d'un element és igual al producte dels cosinus dels elements oposats:

: Si (a) = cosinus (90 ° - A) cosinus (90 ° - c), o el seu equivalent: si (a) = si (A) si (c)

Àrea del triangle esfèric

Un aspecte remarcable és l'àrea del triangle esfèric, que es calcula molt fàcilment a partir dels tres angles:

$\mathrm {Area=R^{2}(\alpha +\beta +\gamma -\pi )} \,$

on $\mathrm {R} \,$ és el radi de l'esfera, i els angles van expressats en radians.

Grup de Bessel

El grup de Bessel són les fórmules bàsiques de la trigonometria esfèrica en la resolució de triangles esfèrics:

cosa = cosb · cosc + sinb · sinc · cos$\alpha$	Fórmula del cosinus
sina · sin$\beta$ = sinb · sin$\alpha$	Fórrmula del sinus
sina · cos$\beta$ = cosb · sinc - sinb · cosc · cos$\alpha$

I, per mutació, el grups corresponents als costats b i c.

Teorema del cosinus

Figura 7 - Triangle esfèric : dimensions reduïdes a, b i c; angles α, β i γ.

En un triangle esfèric ABC (figura 7), el teorema del cosinus s'escriu

$\cos c=\cos a\,\cos b+\sin a\,\sin b\,\cos \gamma$.

Quan el radi de curvatura és molt gran respecte les dimensions del triangle, és a dir quan

$\,a<\!\!<1$,

Aquesta expressió se simplifica per donar la versió euclidiana del teorema del cosinus. Per veure-ho, s'utilitzen els desenvolupaments limitats següents :

$\,\sin a=a+O(a^{3})$, etc.,

$\,\cos a=1-a^{2}/2+O(a^{3})$, etc.

Existeix una identitat similar que enllaça els tres angles :

$\cos \gamma =-\cos \alpha \,\cos \beta +\sin \alpha \,\sin \beta \,\cos c$

Aplicacions

• Càlculs de coordenades:
  • a astronomia (declinació i ascensió recta).

• • a geografia (latitud i longitud).

Bibliografia

• Boyer, Carl Benjamin. A History of Mathematics. 2nd. John Wiley & Sons, Inc., 1991. ISBN 978-0-471-54397-8. 
• Gauchet, L. (1917). Note Sur La Trigonométrie Sphérique de Kouo Cheou-King.
• Joseph, George G. The Crest of the Peacock. Princeton, NJ: Princeton University Press, 2000. ISBN 978-0-691-00659-8. 
• Joseph, George G. The Crest of the Peacock: Non-European Roots of Mathematics. 2a edició. Londres: Penguin Books, 2000. ISBN 978-0-691-00659-8. 
• Katz, Victor J. A History of Mathematics / An Introduction. 2nd. Addison Wesley, 1998. ISBN 978-0-321-01618-8. 
• Katz, Victor J. «The calculus of the trigonometric functions». Historia Mathematica, 14, 4, novembre 1987, pàg. 311–324. DOI: 10.1016/0315-0860(87)90064-4.
• Katz, Victor J. The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press, 2007. ISBN 978-0-691-11485-9. 
• Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.
• O'Connor, J.J., and E.F. Robertson, "Trigonometric functions", Arxiu MacTutor d'Història de les Matemàtiques. (1996).
• O'Connor, J.J., and E.F. Robertson, "Madhava of Sangamagramma", Arxiu MacTutor d'Història de les Matemàtiques. (2000).
• Pearce, Ian G., "Madhava of Sangamagramma", Arxiu MacTutor d'Història de les Matemàtiques. (2002).
• Restivo, Sal. (1992). Mathematics in Society and History: Sociological Inquiries. Dordrecht: Kluwer Academic Publishers. ISBN 1-4020-0039-1

Vegeu també

• Geodèsia
• Geometria no euclidiana
• Geometria hiperbòlica
• Geometria riemanniana
• Triangle esfèric
• Topologia
• Nikolai Lobachevski

Enllaços externs

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Trigonometria esfèrica

• Great Circle Mapper

• Great Circle Calculator Arxivat 2007-06-10 a Wayback Machine.

• Matemática del Círculo Máximo (en inglés)

• Las fórmulas de la Trigonometría Esférica (en español)

Podeu trobar les demostracions del grup de Bessel, i moltes altres relacions trigonomètriques a:

• Wolfram's mathworld: Spherical Trigonometry

• Wolfram's mathworld: Spherical Triangle