Arc (geometria)

Ombrejat en verd, un sector circular de longitud L al llarg del perímetre del cercle

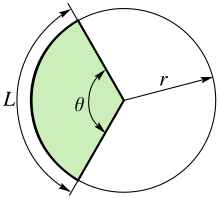
En geometria euclidiana, un arc és un segment tancat d'una corba en un pla bidimensional; per exemple, un arc circular és un segment de la circumferència d'un cercle. Si el segment d'arc ocupa un cercle màxim o una el·lipse màxima, es considera un segment d'arc màxim.

La longitud d'un arc d'un cercle amb radi $r$ i angle $\theta\,\!$ (mesurat en radiants) respecte al centre del cercle és igual a $\theta r\,\!$. Això és perquè

$\frac{L}{\mathrm{circumferencia}}=\frac{\theta}{2\pi}.\,\!$

Si se substitueix "circumferència":

$\frac{L}{2\pi r}=\frac{\theta}{2\pi},\,\!$

i s'aïlla la longitud de l'arc, $L$, s'obté

$L=\theta r.\,\!$

Per a un angle $\alpha$ mesurat en graus, la mida en radiants ve donada per

$\theta=\frac{\alpha}{180}\pi,\,\!$

i per tant la longitud de l'arc és

$L=\frac{\alpha\pi r}{180}.\,\!$