Resolució de triangles
En geometria, la resolució d'un triangle consisteix en la determinació dels diferents elements del triangle (longituds dels costats, mesura dels angles, àrea) a partir d'alguns altres. Històricament, la resolució dels triangles va ser motivada:
- en cartografia, per a la mesura de les distàncies per triangulació ;
- en geometria euclidiana, per a la resolució de nombrosos problemes de geometria;
- en navegació marítima, per la part, que utilitza càlculs de coordenades terrestres i astronòmiques (trigonometria esfèrica).
Avui en dia, la resolució de triangles continua sent utilitzada en un gran nombre de problemes que fan intervenir la triangulació (arquitectura, aixecaments cadastrals, visió estereoscòpica) i la trigonometria en general (astronomia, cartografia). En geometria euclidiana, el coneixement de tres dels elements del triangle, dels quals almenys un ha de ser un costat, és necessari i suficient per a la resolució del triangle (en algun cas pot admetre dues solucions i en algun pot no haver-hi cap solució). En geometria esfèrica o hiperbòlica, el coneixement dels tres angles també és suficient. En la resolució hi intervé la trigonometria, en particular certes relacions clàssiques en el triangle com el teorema del cosinus, el teorema del sinus, el teorema de la tangent i la suma dels angles.
Cas de resolució en geometria euclidiana[modifica]
La resolució d'un triangle en geometria euclidiana utilitza un cert nombre de relacions entre elements del triangle. Les utilitzades més sovint són
- el teorema del cosinus ;
- la fórmula d'Heró ;
- el teorema del sinus ;
- el teorema de la tangent ;
- la suma dels angles d'un triangle val π rad o sigui 180 °,
Tot i que és igualment possible utilitzar altres relacions per a obtenir una solució.
Tot seguit es presenten els casos en funció dels tres elements coneguts entre els tres angles i els tres costats. Les fórmules analítiques es donen per als costats i/o els angles desconeguts, així com l'àrea S. Aquestes fórmules sovint s'han d'adaptar si es pretén fer un càlcul numèric perquè, preses tal qual, donen errors importants d'arrodoniment per als triangles «en agulla», és a dir en els que un dels costats és petit respecte als altres i els triangles « gairebé rectangles», és a dir en els que un dels angles fa aproximadament 90°.
Els tres costats[modifica]
 Es considera un triangle del qual es coneixen els tres costats a, b i c. Els angles es dedueixen a partir del teorema del cosinus i l'àrea, de la fórmula d'Heró :
Es considera un triangle del qual es coneixen els tres costats a, b i c. Els angles es dedueixen a partir del teorema del cosinus i l'àrea, de la fórmula d'Heró :
- , amb
Un angle i els dos costats adjacents[modifica]
 Es considera un triangle del qual es coneix l'angle, així com els dos costats adjacents a i b. L'últim costat s'obté gràcies al teorema del cosinus, els dos angles que manquen pel teorema de la tangent i el complement a π, i l'àrea per la fórmula del producte vectorial :
Es considera un triangle del qual es coneix l'angle, així com els dos costats adjacents a i b. L'últim costat s'obté gràcies al teorema del cosinus, els dos angles que manquen pel teorema de la tangent i el complement a π, i l'àrea per la fórmula del producte vectorial :
Un angle, el costat oposat i un costat adjacent[modifica]
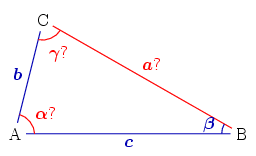 Es considera un triangle del qual es coneix un angle β, així com un costat adjacent d'aquest angle c i el costat oposat b. El segon angle γ s'obté pel teorema del sinus, l'últim angle α per complement a π i l'últim costat pel teorema del sinus :
Es considera un triangle del qual es coneix un angle β, així com un costat adjacent d'aquest angle c i el costat oposat b. El segon angle γ s'obté pel teorema del sinus, l'últim angle α per complement a π i l'últim costat pel teorema del sinus :
Si β és agut i b < c, existeix una segona solució :
Fixeu-vos que la resolució no és possible per a qualsevol conjunt de dades, perquè hi hagi solució cal que es compleixi la següent condició:
- .
Dos angles i el costat comú[modifica]
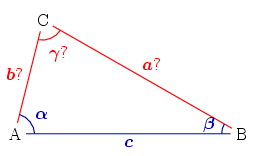 Es considera un triangle del qual es coneix un costat c i els dos angles adjacents α i β. L'últim angle s'obté per complement a π i els altres dos costats pel teorema del sinus:
Es considera un triangle del qual es coneix un costat c i els dos angles adjacents α i β. L'últim angle s'obté per complement a π i els altres dos costats pel teorema del sinus:
Dos angles i un costat no comú[modifica]
Es considera un triangle del qual es coneixen dos angles α i β, així com un costat no comú a aquests dos angles a. L'últim angle s'obté per complement a π i els altres dos costats pel teorema del sinus:
Cas de resolució en geometria esfèrica[modifica]
La resolució d'un triangle en trigonometria esfèrica (geometria no euclidiana) és lleugerament diferent del cas euclidià, ja que el teorema del sinus no permet obtenir un costat de manera unívoca - de manera única el seu sinus. A més, un triangle esfèric del qual es coneixen els tres angles és soluble, contràriament a un triangle del pla euclidià i la solució és única. Les fórmules utilitzades per resoldre un triangle esfèric són :
- les generalitzacions del teorema del cosinus (variants basades en els angles i en els costats) ;
- el teorema de l'Huilier ;
- les analogies de Napier ;
- la suma dels angles d'un triangle val π més l'excés E (=S/R²).
Els tres costats[modifica]
 En un triangle del qual es coneixen els tres costats a, b i c, els angles s'obtenen per la generalització del teorema del cosinus i l'àrea pel teorema de l'Oliaire :
En un triangle del qual es coneixen els tres costats a, b i c, els angles s'obtenen per la generalització del teorema del cosinus i l'àrea pel teorema de l'Oliaire :
- ,
- ,
- ,
- on .
Un angle i els dos costats adjacents.[modifica]
 En un triangle on es coneixen dos costats a i b i l'angle que formen, l'últim costat s'obté pel teorema del cosinus generalitzat i els dos angles restants per les analogies de Napier :
En un triangle on es coneixen dos costats a i b i l'angle que formen, l'últim costat s'obté pel teorema del cosinus generalitzat i els dos angles restants per les analogies de Napier :
- ,
- ,
- ,
- .
Un angle, el costat oposat i un costat adjacent[modifica]
 Es considera un triangle del qual es coneixen un angle β, un costat adjacent c i el costat oposat b. L'angle γ s'obté pel teorema del sinus i els elements restants per les analogies de Napier. Només hi ha solució si
Es considera un triangle del qual es coneixen un angle β, un costat adjacent c i el costat oposat b. L'angle γ s'obté pel teorema del sinus i els elements restants per les analogies de Napier. Només hi ha solució si
- .
Llavors
- ,
- ,
- .
Hi ha una altra solució quan b > c i γ és agut :
- , etc.
Dos angles i el costat comú[modifica]
 En un triangle on es coneixen dos angles α i β, així com el costat comú a aquests angles c, l'últim angle s'obté pel teorema del cosinus i els dos últims costats per les analogies de Napier. Les fórmules per a l'angle que manca i els costats s'assemblen a les del cas de resolució complementària (un angle i els dos costats adjacents) :
En un triangle on es coneixen dos angles α i β, així com el costat comú a aquests angles c, l'últim angle s'obté pel teorema del cosinus i els dos últims costats per les analogies de Napier. Les fórmules per a l'angle que manca i els costats s'assemblen a les del cas de resolució complementària (un angle i els dos costats adjacents) :
- ,
- ,
- ,
- .
Dos angles i un costat no comú[modifica]
 Es considera un triangle en el qual es coneixen dos angles α i β, així com un costat oposat a un d'aquests angles a. El costat b es troba pel teorema del sinus i els elements restants per les analogies de Napier. Fixeu-vos en la similitud entre les equacions següents i el cas de resolució complementària (un angle, el costat oposat i un costat adjacent) :
Es considera un triangle en el qual es coneixen dos angles α i β, així com un costat oposat a un d'aquests angles a. El costat b es troba pel teorema del sinus i els elements restants per les analogies de Napier. Fixeu-vos en la similitud entre les equacions següents i el cas de resolució complementària (un angle, el costat oposat i un costat adjacent) :
- ,
- ,
- ,
- .
Si a es agut i α > β, existeix una altra solució :
- , etc.
Els tres angles[modifica]
 En el cas en què els tres angles són coneguts, els costats s'obtenen per una variant del teorema del cosinus per als angles. Les fórmules que donen els costats són semblants a les del cas de resolució complementària (els tres costats coneguts) :
En el cas en què els tres angles són coneguts, els costats s'obtenen per una variant del teorema del cosinus per als angles. Les fórmules que donen els costats són semblants a les del cas de resolució complementària (els tres costats coneguts) :
- ,
- ,
- .
Exemples d'aplicació[modifica]
Triangulació[modifica]

La figura 1 de la dreta indica un mètode de determinació de la distància d'un vaixell per triangulació : a partir de dos punts dels quals es coneix la distància l, es mesuren els angles de la visual del vaixell respecte de la línia que uneix els dos punts. De les mesures efectuades, és possible deduir-ne la distància gràficament posant els elements coneguts en un gràfic amb una escala idònia. D'altra banda, es pot trobar una fórmula analítica resolent el triangle del qual es coneixen dos angles i el costat comú :
- .

Una altra possibilitat és la mesura de l'alçada h d'una muntanya des d'una vall mesurant la seva alçada angular α i β en dos punts de distància coneguda l. La figura 2 de la dreta dona un cas simplificat en el qual els punts de mesura i la projecció del cim sobre el sòl són alineats. L'alçada de la muntanya pot ser determinada gràficament o bé analíticament per resolució del triangle (triangle del qual es coneixen dos angles i el costat comú) :
- .
En la pràctica el mètode de resolució xoca amb algunes dificultats : el terreny no és per força pla, el que requereix una estimació del pendent entre els dos punts; el cim real no és per força observable des de la planura i el punt més alt observable varia de posició entre els dos punts d'observació per efecte de tangència; els diferents elements del relleu han de ser triangulats de d'un en un a partir de les cotes el que acumula els errors de mesura. Així, la cartografia per satèl·lit ha modificat en diversos metres els valors tradicionals considerats de certs cims Malgrat aquestes dificultats, al segle xix, Friedrich Georg Wilhelm von Struve va fer construir l'arc geodèsic de Struve, una cadena d'indicacions geodèsiques travessant Europa al llarg de 2.800 km de la Noruega al Mar Negre i de la qual l'objectiu era determinar la mida i la forma de la terra : el 1853, el científic obté una mesura del meridià terrestre a 188 m prop (2×10-5) i de l'aixafament de la terra de l'1%.[1]
Distància entre dos punts del globus[modifica]
 Es consideren dos punts del globus A i B de latituds respectives λA i λB, i de longituds LA i LB. Per determinar la seva distància es considera el triangle ABC, on C és el pol. En aquest triangle es coneixen:
Es consideren dos punts del globus A i B de latituds respectives λA i λB, i de longituds LA i LB. Per determinar la seva distància es considera el triangle ABC, on C és el pol. En aquest triangle es coneixen:
La resolució del triangle en el cas on un angle i els dos costats adjacents són coneguts permet obtenir
- ,
on R és el radi de la terra.
Vegeu també[modifica]
- Triangle
- Teorema del cosinus
- Teorema del sinus
- Teorema de la tangent
- Fórmula d'Heró
- Teorema de l'Huilier
- Triangulació
- Trigonometria
- Funcions trigonomètriques
- Trigonometria esfèrica
Referències[modifica]
- ↑ (anglès) J.R. Smith, The Struve Geodesic Arc
Enllaços externs[modifica]
- Resolució de triangles, Permet la resolució de triangles plans amb tota mena de dades no només lognituds de costats i angles si no també amb altures, mitjanes, radi de la circumferència circumscrita...
- Triangle calculator, permet la resolució d'un triangle pla. (anglès)
- Trigonometria esfèrica al lloc web de Math World (anglès)

























































