Sèrie de Fourier
En matemàtiques, una sèrie de Fourier descompon una funció periòdica en una suma de funcions oscil·latòries simples: el sinus i el cosinus. L'estudi de les sèries de Fourier forma part de l'anàlisi de Fourier. Les sèries de Fourier foren introduïdes per Joseph Fourier (1768–1830) amb l'objectiu de solucionar una equació de la calor en un plat metàl·lic. Va suposar una revolució dins les matemàtiques, forçant els matemàtics a reexaminar els fonaments de les matemàtiques i portant a la descoberta de teories modernes com la Integral de Lebesgue. Joseph Fourier va ser el primer que va estudiar tals sèries sistemàticament, publicant els seus resultats inicials el 1807 i 1811. Aquesta àrea d'investigació sovint s'anomena anàlisi harmònica.
Amb aquesta eina podrem analitzar un senyal periòdic en termes del seu contingut freqüencial o espectre. Ens permetrà establir la dualitat entre temps i freqüència, així, operacions realitzades en el domini temporal tindran també el seu dual en el domini freqüencial.
La sèrie de Fourier té aplicacions en moltes branques de l'enginyeria, a més de ser una eina molt útil en la teoria matemàtica abstracta. Àrees d'aplicació inclouen anàlisi de les vibracions, acústica, òptica, processament del senyal, processament d'imatge, etc. En enginyeria, per al cas dels sistemes de telecomunicacions, i a través de l'ús dels components espectrals de freqüència d'un senyal donat, es pot optimitzar el disseny d'un sistema per al senyal portador d'aquest.
Evolució històrica[modifica]
Context[modifica]
Donada una funció periòdica , per exemple de període , es desitja escriure-la com una combinació en la qual intervinguin únicament sinus i cosinus, que són les funcions de període simples més conegudes:[1]
Aquesta sèrie rep el nom de sèrie trigonomètrica o Sèrie de Fourier.

El problema de la representació d'una funció mitjançant una sèrie trigonomètrica sorgeix de la resolució d'equacions en derivades parcials. Pels voltants del 1750, J. d'Alembert, D. Bernoulli i L. Euler van estudiar l'equació d'ones que governa el problema de la corba vibrant, un problema plantejat i estudiat per B. Taylor que havia obtingut solucions en forma de funcions sinusoidals. D'Alembert va donar una solució molt general i Euler va provar que si a l'instant inicial de la forma de la corda apareix una combinació finita de sinus, llavors esdevindria el mateix que en qualsevol altre instant posterior, publicant molt més tard, el 1777, les fórmules que permetien calcular els coeficients de la combinació. El 1753, Bernoulli va utilitzar aquesta representació per resoldre el problema de la corda vibrant per una posició inicial qualsevol, però la seva solució va suscitar molta controvèrsia. Va ser J. B. Fourier qui va reprendre un altre cop les idees d'Euler i Bernoulli i va obtenir resultats molt ajustats els experiments, col·locant l'estudi de les sèries trigonomètriques – que avui dia porten el seu nom - en el centre de l'escenari matemàtic del segle xix. La teoria de les sèries de Fourier va ser una forta influència per l'anàlisi matemàtica i és avui una eina bàsica de l'enginyeria de telecomunicacions.
Periodicitat[modifica]
En el camp de la teoria del senyal i la comunicació, quan t és la variable temporal, es diu que f(t) és un senyal periòdic en temps continu, i quan aquesta representació en sèrie de funcions trigonomètriques és correcta, es pot dir que s'ha descompost el senyal en harmònics. A continuació s'estudia més a fons com calcular els coeficients, alguns exemples i algunes propietats, i també la notació exponencial de les sèries de Fourier. Finalment, es consideraran senyals periòdics perquè resultaran més senzills pel seu estudi. Recordem que:
- és periòdica de període
si és tal que
Pels casos en què les funcions no compleixen la periodicitat s'introdueix la Transformada de Fourier, que, encara que comparteix moltes característiques i propietats amb la Transformada de Laplace, s'utilitza en contextos diferents.
Definició[modifica]
- Les Sèries de Fourier descriuen els senyals periòdics com a combinació de senyals harmònics (sinusoidals).
- Amb aquesta eina es pot analitzar un senyal periòdic en termes del seu contingut freqüencial o espectre.
- Permet establir una dualitat entre temps i freqüència, de manera que les operacions realitzades en el domini temporal tenen el seu dual en el domini freqüencial.
- La forma trigonomètrica de les Sèries de Fourier permet descriure una funció periòdica x(t) de període T (freqüència fonamental).
Forma general[modifica]
Sigui f(x) una funció complexa f definida en el domini dels nombres reals, on t , definida a trossos, periòdica en f(t) amb període T, i de quadrat integrable a l'interval de a de durada T:
amb , llavors es definex la sèrie trigonomètrica de Fourier:
on els seus coeficients venen donats per les següents expressions:
- , on n és el nombre d'harmònics de la funció f,
- , és la part parella dels coeficients de Fourier de la funció f,
- , és la part senar dels coeficients de Fourier de la funció f.
Forma canònica[modifica]
En el cas especial de tenir un període T = 2π, s'obté que .
En aquest cas, els coeficients de la Sèrie de Fourier es redueixen, arribant a una expressió particularment simple:
on
Forma exponencial[modifica]
Per la identitat d'Euler per l'exponencial complexa, operant adequadament, si
La sèrie de Fourier es pot expressar com la suma de dues sèries:
De manera més compacta:
Forma del període[modifica]
La forma pel període T, es pot derivar fàcilment a la forma canònica amb el canvi de la variable definida per . Per tant, les dues formulacions són equivalents. Tot i això, a la pràctica la forma pel període T s'utilitza de forma majoritària degut a la seva aplicació directa. A la teoria, sempre és preferible utilitzar la forma canònica atès que és més elegant i més fàcil d'interpretar matemàticament.
Propietats[modifica]
- Superposició
- Derivada
- Integral
- Retard
- Escalat
- harmònics en
- Modulació
- Convolució
Exemple[modifica]
Escriure la Sèrie de Fourier corresponent a la funció f definida a continuació, a l'interval < x < :
Els coeficients de Fourier són:

on n =1, 2,... Per tant, a l'interval ,
Es veu així per què aquesta Sèrie de Fourier convergeix a f(x) quan . Així mateix aquesta sèrie representa l'extensió periòdica de la funció f indicada a les línies de punts de la Fig.1. La funció periòdica és discontínua en els punts . La teoria mostrarà que la suma de la sèrie a cadascun d'aquests punts ha de ser . Una petita indicació de la convergència de la sèrie a f(x), és que es poden sumar alguns termes de la sèrie per composició d'ordenades. Es trobarà, per exemple, que la gràfica de la funció és una aproximació ondulada de la gràfica de la Fig. 1 .
Convergència de la Sèrie de Fourier[modifica]
Sigui contínua a trossos i periòdica de període T, i sigui
on és la seva Sèrie de Fourier. P.G.L. Dirichlet el 1829 va demostrar satisfactòriament que un grup específic de funcions, són iguals a la suma de les seves sèries de Fourier.
Condicions de Dirichlet[modifica]
Sigui una funció periòdica de període T. Llavors, f satisfà les condicions de Dirichlet si cada període de la funció és continu excepte un nombre finit de discontinuïtats de salt. En particular es pot demostrar, que si una funció periòdica és tal que ella i la seva derivada estan definides i són contínues excepte en un nombre finit de discontinuïtats de salt, llavors aquesta funció verifica les condicions de Dirichlet.
Teorema de convergència de Dirichlet[modifica]
Sigui una funció periòdica de període T que satisfà les condicions de Dirichlet i sigui
on és la seva Sèrie de Fourier.
- Si f és contínua en un punt t, llavors la Sèrie de Fourier convergeix en aquest punt a f(t), o sigui
-
- Si f té una discontinuïtat de salt en un punt t, llavors la sèrie convergeix en aquest punt vers el punt mitjà del salt, o sigui
on indica el límit de f a t per l'esquerra i indica el límit de f a t per la dreta.
El teorema indica que si f satisfà les condicions de Dirichlet i es redefineix el valor de f a cada punt de la discontinuïtat com el punt mitjà del salt, és a dir , llavors la suma de la Sèrie de Fourier coincideix amb f(t) a cada . Suposant que això es compleixi, es pot afirmar que la condició s'acompleix.
Convergència uniforme de les sèries de Fourier[modifica]
Si es compleix que la funció , de període a, és diferenciable en l'interval [0,a], excepte potser en un nombre finit de punts, i la derivada és contínua, aleshores:[2]
1- La sèrie de Fourier de s'obté derivant terme a terme els coeficients de la sèrie de Fourier de .
2- Els coeficients de Fourier de satisfan:
3- La sèrie de Fourier de convergeix uniformement cap a en .[3][4]
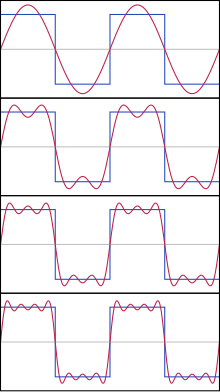
Fenomen de Gibbs[modifica]

El teorema de Dirichlet diu que en els punts de discontinuïtat, la gràfica de la suma de la Sèrie de Fourier passa per un punt entremig del salt. Si es dibuixen les sumes parcials es veu que els voltants dels punts de discontinuïtat es redueix la velocitat de convergència de la sèrie i que la gràfica de la suma parcial oscil·la al voltant de la gràfica de la funció. Quan augmenta el nombre de termes, les oscil·lacions es condensen a ambdós costats del punt, però la seva amplitud no decreix.[5] Això es coneix com el fenomen de Gibbs, en honor de J.W. Gibbs, que el 1899 va provar que l'amplitud l'oscil·lació a cada costat de la gràfica d'una funció tendeix a ser vegades la mida del salt, és a dir, aproximadament el 9%.[6]
Aplicacions Sèrie de Fourier[modifica]
- Generació de formes d'ona de corrent o tensió elèctrica per mitjà de la superposició de sinusoides generades per oscil·ladors electrònics d'amplitud variable de les quals les freqüències ja estan determinades.
- Anàlisi en el comportament harmònic d'un senyal.
- Reforçament de senyals.
- Estudi de la resposta en el temps d'una variable circuital elèctrica on el senyal d'entrada no és sinusoidal o cosinusoidal, mitjançant l'ús de les transformades de Laplace i de la solució en règim permanent sinusoidal en el domini de la freqüència.
- La resolució d'algunes equacions diferencials en derivades parcials permeten solucions particulars en sèries de Fourier fàcilment computables, i per obtenir solucions pràctiques, en la teoria de la transmissió de la calor, la teoría de plaques, etc.
Algunes propietats del desenvolupament en Sèrie de Fourier[modifica]
Derivació de les sèries de Fourier[modifica]
Si f és una funció contínua i periòdica de període T i la seva derivada f' verifica les condicions de Dirichlet, llavors, la sèrie de Fourier de f es pot derivar terme a terme de manera que si
aleshores
per cada
Integració de les sèries de Fourier[modifica]
Si f és una funció contínua i periòdica de període T que verifica les condicions de Dirichlet, llavors, la sèrie de Fourier de f es pot integrar terme a terme de manera que si
i , aleshores
S'ha d'anar amb compte, ja que al terme fa que el membre de la dreta no sigui una Sèrie de Fourier. El teorema ens proporciona el desenvolupament en sèrie de Fourier de la funció g definida a per i repetida periòdicament.
Igualtat de Parseval[modifica]
Si f és una periòdica de període T que verifica les condicions de Dirichlet, i sigui
la seva Sèrie de Fourier. Aleshores
Quan f és un senyal periòdic de període fonamental T, aquesta igualtat es pot interpretar de la següent manera. La integral s'anomena mitjana quadràtica o potència mitjana de f.
Notació complexa de la Sèrie de Fourier[modifica]
Forma general[modifica]
Hem vist dues maneres d'expressar la Sèrie de Fourier d'una funció periòdica de període T: en termes de sinus i cosinus
o bé en termes l'amplitud i fase
on i els coeficients d'aquestes expressions estan relacionades de la següent manera: i per n=1,2...
-
- i
o bé
- i
A moltes aplicacions, en particular a la teoria de senyals i comunicacions, és més útil una tercera expressió, anomenada notació complexa de la sèrie de Fourier, que consisteix amb la utilització d'exponencials complexos en lloc de i . Per construir-les, substituïm les expressions
-
- i
a la sèrie , obtenint
Escrivint
- , ,
separant els termes que tenen índex negatiu dels que tenen índex positiu i ordenant-los, la Sèrie de Fourier queda
que s'anomena notació complexa de la Sèrie de Fourier de f. Els nombres són els coeficients de Fourier de la notació complexa i es poden calcular de forma directa
- per
En canvi si el que tenim són els coeficients de la notació complexa, aleshores els coeficients de Fourier i , les amplituds i les fases venen donades per
- i
Aleshores, veiem, que una funció periòdica és par quan els seus coeficients de Fourier complexos són reals i que és imparell quan els seus coeficients complexos de Fourier són imaginaris purs. Quan f(t) és un senyal periòdic de període fonamental T, les components de la notació complexa es donen en freqüència
Propietats[modifica]
Suposarem que f i g són funcions periòdiques de període T (reals o complexes) que verifiquen les condicions de Dirichlet, els quals desenvolupats en notació complexa de la Sèrie de Fourier, són, respectivament,
- i
on
- Linealitat: si p i q son nombres complexos
- Translació en el temps: és un nombre real.
- i tenen el mateix espectre d'amplituds però fase diferent.
- Escalat en el temps: p és un nombre real, aleshores la funció f(pt) és periòdica de període T i freqüència .
- i tenen les mateixes amplituds y fases però corresponen a freqüències diferents
- Convolució
- Multiplicació
- Forma complexa de la igualtat de Parseval
- Quan f(t) és un senyal periòdic de període fonamental T, aquesta igualtat ens diu que la potència mitjana del senyal és . Per aquest fet, la representació dels valors quan situem les freqüències a l'eix d'abscisses s'anomena espectre discret de potències.
Exemple[modifica]


Els coeficients complexos de Fourier d'un tren de polsos rectangulars, donats com l'extensió periòdica de la funció definida a l'interval de per
són
Els valor de són reals, el que correspon el fet que la funció sigui parella, així doncs el seu espectre de fases és per cada n. La funció
s'anomena funció de mostreig (‘sa' prové de la paraula anglesa sampling) i és molt important a la teoria de senyals, precisament perquè els coeficients complexos de Fourier del tren de polsos rectangulars d'aquest exemple es poden expressar com:
A vegades, en lloc de la funció de mostreig es treballa amb una altra funció, anomenada sinus cardinal que es defineix com
Enginyeria[modifica]
L'anàlisi de senyals en el domini de la freqüència es realitza a través de les sèries de Fourier, ja que és molt comú, reemplaçar la variable x per ωt, resultant les components:
Per tant:
Espectre d'una funció periòdica[modifica]
Sigui una funció periòdica, de període , que es pot escriure com:
Aleshores direm que la sèrie de Fourier anterior és la descomposició espectral de la funció . El conjunt de coeficients i o, el conjunt de coeficients s'anomena l'espectre de la funció . L'espectre d'una funció, per tant, conté tota la informació d'aquesta i, si considerem la funció com la superposició d'ones planes, l'espectre de la funció és el conjunt d'amplituds d'aquestes ones.
Exemples[modifica]
Sigui la funció de període ,
El seu espectre és, com hem vist a l'exemple d'abans,
o, equivalentment
Considerem un altre exemple senzill; sigui la funció i .
El seu espectre és:
Referències[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Sèrie de Fourier |
- ↑ E. Boyce, William; C. DiPrima, Richard. Elementary Differential Equation and Boundary Value Problem (en anglès). 10a. JohnWiley & Sons, Inc, 2012, p. 597. ISBN 978-0-470-45831-0.
- ↑ G. Gasquet, P.Witomski; Fourirer Analysis and Applications. Springer-Verlag, 1999; p.45.
- ↑ Hardy, G.H.; Rogosinski, W. «Chapter IV: Convergence of Fourier series». A: Fourier Series. Courier Dover Publications. Cambridge University Press, 1999, p. 37. ISBN 0486406814.
- ↑ Jahnke, H. N.. «6.5 Convergence of Fourier series». A: A History of Analysis. American Mathematical Society, 2003, p. 178. ISBN 0821826239.
- ↑ Florinsky, Igor. Digital Terrain Analysis in Soil Science and Geology. Academic Press, 2011, p. 88. ISBN 0123850371. Veure il·lustració a "Figure 5.8: Approximation of a square wave".
- ↑ Jerri, Abdul J. The Gibbs Phenomenon in Fourier Analysis, Slines and Wavelet Approximations. Springer, 1998. ISBN 0792351096.



![{\displaystyle f(t)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }[a_{n}\cos(nt)+b_{n}\sin(nt)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0311913624a865e1fa9386e5f9b8ccca589ce33f)









![{\displaystyle f(t)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\,{\big [}a_{n}\cos(\omega _{n}t)+b_{n}\sin(\omega _{n}t){\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/454321e7eccd24ec0f7b27e420fbcf714644ce98)










![{\displaystyle \alpha x_{p}(t)+\beta y_{p}(t)\leftrightarrow \alpha X_{s}[k]+\beta Y_{s}[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bafc23e0b7d22214c8aaef3e10d1da9c331bd0e0)
}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdff5bcd724d682a6b00ce514dc1e5e4756dc2dd)
![{\displaystyle \int _{0}^{t}x_{p}(t)\,dt\leftrightarrow {\frac {X[k]}{jk2\pi f_{0}}}+C(k\neq 0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88551dd23a82031b5dd0931ea4b7dbfdcfdde89e)
![{\displaystyle x_{p}(t-\alpha )\leftrightarrow X_{s}[k]e^{-j2k\pi f_{0}\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c11efa1ba246addaa0926a80542c7711f0f06e2)
![{\displaystyle x_{p}(t)\leftrightarrow \ X_{s}[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe2ba3ec82610e25b2ed4aec125a0bd897170d80)

![{\displaystyle x_{p}(-t)\leftrightarrow \ X_{s}[-k]=X_{s}^{*}[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb29613811ea7987477ff80c13fb581a38e72995)
![{\displaystyle \cos(m2\pi f_{0}t)x_{p}(t)\leftrightarrow {\frac {1}{2}}{\big \{}X_{s}[k-m]+X_{s}[k+m]{\big \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9031211368e093a61a220a68fe60712200922fbe)
![{\displaystyle {\frac {1}{2}}{\big \{}x_{p}(t+\alpha )+x_{p}(t-\alpha ){\big \}}\leftrightarrow \cos(2\pi f_{0}\alpha )X_{s}[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea919fe4e998db3311d23f2b0c637be707b3598d)
![{\displaystyle x_{p}(t)y_{p}(t)\leftrightarrow X_{s}[k]*Y_{s}[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a823bd7ddbd39eb80a003e69e8ef82dfa9507e17)
![{\displaystyle x_{p}(t)\bullet y_{p}(t)\leftrightarrow \ X_{s}[k]Y_{s}[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c609a57fcd6456703fb049715054fc8c00ece40f)







![{\displaystyle =\left[{\frac {\cos nx+nx\sin nx}{\pi n^{2}}}\right]_{0}^{\pi }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a3ba5f807b8baec95e3cb047dd716a49490b8f8)


![{\displaystyle =\left[{\frac {\sin nx-nx\cos nx}{\pi n^{2}}}\right]_{0}^{\pi }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbee66b8abee52fd9e092ed47ef42f711822b0ab)


![{\displaystyle f(x)\sim {\frac {\pi }{4}}+\sum _{n>0}\left[{\frac {(-1)^{n}-1}{\pi n^{2}}}\cos nx-{\frac {(-1)^{n}}{n}}\sin nx\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a00c377d6d2282c45d77065493aebba778db8f47)





![{\displaystyle f(t)\sim {\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }[a_{n}\cos(n\omega t)+b_{n}\sin(n\omega t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6079e201b96ee45f110db8def38c86cde48d0d37)

![{\displaystyle f:[0,T]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/03afa0f78ac1185e86da454ced0d1c1c604001e9)
![{\displaystyle {\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }[a_{n}\cos(n\omega t)+b_{n}\sin(n\omega t)]=f(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38268e2adc70aeecf41b946fbaf7ddd28368a4a1)
![{\displaystyle {\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }[a_{n}\cos(n\omega t)+b_{n}\sin(n\omega t)]={\frac {f(t^{-})+f(t^{+})}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2a403777e1c93580f47eaa2e60f1dd639c21fd8)









![{\displaystyle f(t)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }[a_{n}\cos(n\omega t)+b_{n}\sin(n\omega t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ea21cdc75a69be61463791d38c0acbd08473516)
![{\displaystyle f'(t)\sim \sum _{n=1}^{\infty }[nb_{n}\omega \cos(n\omega t)+na_{n}\omega \sin(n\omega t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/add98766d6a7ee8ba29bdd4b58aa1314df45833f)
![{\displaystyle t_{0},t\in \left[{\frac {-T}{2}},{\frac {T}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab0a6da86dfb3f1edb8c0f7ffc04c2df35cb5c5d)
![{\displaystyle \int _{t_{0}}^{t}f(\tau )\,d\tau ={\frac {1}{2}}a_{0}(t-t_{0})+\sum _{n=1}^{\infty }\left[{\frac {b_{n}(\cos(n\omega t_{0})-\cos(n\omega t))}{n\omega }}+{\frac {a_{n}(\sin(n\omega t)-\sin(n\omega t_{0}))}{n\omega }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3af209986c2ad8866e31b58696751a73045a5bf3)

![{\displaystyle \left[{\frac {-T}{2}},{\frac {T}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1287d18fe599ae9ab09e3a590d6b7428f33b484e)

![{\displaystyle {\frac {1}{T}}\int _{0}^{T}[f(t)]^{2}\,dt={\frac {1}{4}}a_{0}^{2}+{\frac {1}{2}}\sum _{n=1}^{\infty }[a_{n}^{2}+b_{n}^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0972d5f4a0f41147f249a0d5df73010f699d47c)
![{\displaystyle P={\frac {1}{T}}\int _{0}^{T}[f(t)]^{2}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8d34e6c5af33b005713c9f1648b87340be0c055)



![{\displaystyle \phi _{n}=\arctan \left({\frac {-b_{n}}{a_{n}}}\right)\in (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0df2cf9395ea12a620efdfd3f08a2e2f233bcb6)







![{\displaystyle {\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }[a_{n}\cos(n\omega t)+b_{n}\sin(n\omega t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f324e969f0302bc24e28a875cc480610cbe3c473)
![{\displaystyle f(t)\sim {\frac {a_{0}}{2}}+{\frac {1}{2}}\sum _{n=1}^{\infty }[(a_{n}-jb_{n})e^{jn\omega t}+(a_{n}+jb_{n})e^{-jn\omega t}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/159a467b6faece97797f2a3c7ee155cda43c80f4)










![{\displaystyle \phi _{n}=\arg(c_{n})\in (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba182701763a907fbbe71ac6bc9a17287cdafbe4)




























![{\displaystyle \{C_{n}\}={\Big \{}{\frac {\pi }{4}}{\Big \}}\cup {\Bigg \{}{\frac {1}{2n}}{\bigg [}ie^{in\pi }+{\frac {1}{\pi n}}(e^{in\pi }-1){\bigg ]}{\Bigg \}},n\in \mathbb {Z} ^{*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2dc9f5b39b42878296643259cd09293aec4db0f)
![{\displaystyle f(t)={\begin{cases}0&{\text{si}}&t\in {\Big (}-1,-{\frac {1}{2}}{\Big )}\cup {\Big (}{\frac {1}{2}},1{\Big ]}\\1&{\text{si}}&t\in {\Big (}-{\frac {1}{2}},{\frac {1}{2}}{\Big )}\\{\frac {1}{2}}&{\text{si}}&t=\pm {\frac {1}{2}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3aeaba2fcc0272a71b405904d14fa1768dfd4bc6)


