Teorema de Pitàgores
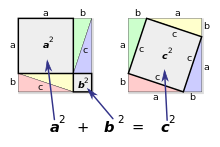
El teorema de Pitàgores o teorema de Pitàgoras, en el seu enunciat habitual, estableix que en un triangle rectangle la suma dels quadrats dels catets (els costats que formen l'angle recte) és igual al quadrat de la hipotenusa (l'altre costat).[1]
El recíproc també es compleix, és a dir: en un triangle, si la suma dels quadrats de les longituds dels costats més curts és igual al quadrat de la longitud del costat més llarg, llavors l'angle comprès entre els dos costats més curts és un angle recte.[2]
El teorema es pot escriure com una equació que relaciona les longituds dels costats a, b, i c, sovint anomenada l'equació de Pitàgores:[3]
on c representa la longitud de la hipotenusa, i a i b representen les longituds dels altres dos costats.
El teorema de Pitàgores deu el nom al matemàtic grec Pitàgores, al que segons la tradició se li atribueix el seu descobriment i la demostració,[4][5] encara que sovint s'argumenta que el coneixement del teorema era ja anterior. Hi ha proves que els matemàtics babilonis coneixien la fórmula, encara que ens ha arribat molt poca informació sobre l'ús que en feien.[6][7]
El teorema es refereix tant a les àrees com a les longituds, o pot dir-se que a les dues àrees i a les interpretacions mètriques.[8][9] Algunes demostracions del teorema es basen en una interpretació, algunes sobre l'altra, utilitzant tècniques algebraiques i geomètriques.[10] El teorema pot ser generalitzat de diverses maneres, incloent espais de dimensió superior, als espais no euclidians, als objectes que no són triangles rectangles i, de fet, als objectes que no són en tots els triangles, però són n-dimensionals sòlids. El teorema de Pitàgores ha despertat l'interès fora de les matemàtiques com un símbol de l'hermetisme de les matemàtiques, de la mística, o el poder intel·lectual; referències en la literatura popular, obres de teatre, abunden els musicals, cançons, segells i en els dibuixos animats.
Història[modifica]
Orígens[modifica]

Els rastres més antics de la relació entre les longituds dels costats d'un triangle rectangle, un matemàtic considerà erròniament que es troben en la inscripció de ternes pitagòriques. Es tracta de ternes de nombres naturals (a, b, c) que satisfan la relació , referint-se a tauletes babilònies, sobretot a la tauleta Plimpton 322 datada del XVIII aC, o sigui més de 1000 anys abans de Pitàgores.[11][12][13] Alguns pretenen fins i tot trobar-ne a megàlits datats del segle XXV aC a la Gran Bretanya.[14]
Entre aquests triplets, el més petit és 3-4-5. Correspon a les dimensions d'un triangle rectangle del qual Plutarc conjectura una interpretació simbòlica des de l'antic Egipte.[15] Aquest triangle es pot formar amb l'ajuda d'una corda de tretze nusos que romandria una de les eines dels geòmetres fins al final de l'edat mitjana.[16]
Però d'una banda, la utilització d'aquesta corda amb nusos no indica per força el coneixement del fet que l'angle format és matemàticament un angle recte; d'altra banda l'inventari de triplets pitagòrics ha pogut ser trobat en un marc aritmètic fora del context geomètric. Finalment, perquè la conjectura s'erigeixi en teorema, cal que la relació sigui demostrada, i no només en alguns casos particulars.
Formulacions[modifica]
El teorema, acompanyat d'una demostració, apareix al començament del segle III en els Elements d'Euclides (proposició XLVII) amb la següent forma:
«En els triangles rectangles el quadrat del costat oposat a l'angle recte és igual a la suma dels quadrats dels costats que comprenen a l'angle recte.»
El seu recíproc és la proposició XLVIII:
«Si en un triangle el quadrat d'un dels costats és igual a la suma dels quadrats dels dos costats restants, aleshores l'angle comprès pels dos costats restants del triangle és recte.»

Els comentaris de Procle (al voltant de l'any 400) semblen indicar que Euclides no hauria fet més que transcriure una demostració més antiga que Procle atribueix a Pitàgores. Tanmateix, les proves històriques de la vida de Pitàgores són tan rares que no se li pot atribuir amb certesa la paternitat d'aquesta demostració.
Paral·lelament al desenvolupament de les matemàtiques gregues, el teorema apareix a la Xina en el Zhoubi suanjing («El Gnòmon dels Zhou»), una de les obres matemàtiques xineses més antigues. Aquest últim, escrit probablement durant la dinastia Han (-206 a 220), reagrupa tècniques de càlcul que daten de la dinastia Zhou segle X aC al 256 aC. El teorema o procediment s'hi enuncia de la manera següent:
«Reunint l'àrea (mi) de la base (gou) i l'àrea de l'alçada (gu) s'engendra l'àrea de la hipotenusa.»
Però la qüestió és saber si aquest teorema o procediment és proveït o no d'una demostració. Sobre aquest punt hi ha divisió d'opinions.[17] El teorema, sota el nom de Gougu (a partir de les paraules «base» i «altitud»), és reprès en el Jiuzhang suanshu (Els nou capítols de les arts matemàtiques (九章算术) -100 a 50), amb una demostració, utilitzant una partició i una reconstitució, que no s'assembla en res a la d'Euclides i que prova l'originalitat del camí xinès.
A l'Índia, cap al 300 aC, es troba el rastre d'una demostració numèrica de la propietat (prova efectuada sobre nombres particulars però que es pot generalitzar fàcilment).
Més tard se n'han inventat moltes altres, utilitzant eines matemàtiques variades. Leonardo da Vinci i fins i tot el president americà James Garfield n'han proposat.
Conseqüències[modifica]
El teorema de Pitàgores podria haver estat a l'origen de la noció de grandàries incommensurables, premissa dels nombres irracionals. En efecte, demostra[18] que un quadrat el costat del qual serveix d'unitat té una diagonal amb una longitud el quadrat de la qual val 2. Ara bé, cap fracció de nombres naturals no té quadrat igual a 2. La construcció geomètrica d'una relació «privada de raó» anava en contra de la visió del món de l'escola pitagòrica.[19]

La recerca exhaustiva dels triplets pitagòrics, motivada per la construcció de triangles rectangles les longituds dels costat dels quals són commensurables, s'ha constituït plenament en un problema aritmètic. Obre la porta a la recerca de triplets que satisfan una equació més general: , on l'exponent és un enter superior a 2. L'absència de solució quan l'exponent és superior o igual a 3 és la conjectura de Fermat, que no va ser definitivament demostrada fins a més de tres segles més tard per Andrew Wiles.
Finalment, s'ha demostrat que el teorema de Pitàgores és equivalent a l'axioma de les paral·leles.[20]
Validació física[modifica]
En derivar-se el teorema de Pitàgores dels axiomes de la geometria euclidiana, la seva validesa al món real s'ha pogut posar en qüestió amb el caràcter no euclidià de l'espai físic. El matemàtic Carl Friedrich Gauss va considerar aquesta hipòtesi prop d'un segle abans del naixement de la teoria de la relativitat general, segons una llegenda.[21] Hauria mesurat els angles d'un triangle format per tres ciutats de la regió de Hannover per tal de verificar si la suma dels seus angles constituïa efectivament un angle pla.
Altres formes[modifica]
Com s'assenyala en la introducció, si c denota la longitud de la hipotenusa i a i b denoten les longituds dels altres dos costats, el teorema de Pitàgores es pot expressar com l'equació de Pitàgores:
Si la longitud de a i b són conegudes, llavors c es pot calcular de la següent manera:
Si la longitud de c i una cama (a o b) són coneguts, la longitud de l'altra cama es pot calcular amb les següents equacions:
o
L'equació de Pitàgores estableix una relació simple entre els tres costats d'un triangle rectangle de manera que, si es coneix la longitud de qualsevol dels dos costats, llavors es pot trobar la longitud del tercer costat. Una generalització d'aquest teorema és la llei dels cosinus, que permet el càlcul de la longitud del tercer costat de qualsevol triangle, tenint en compte les longituds de dos costats i la mida de l'angle entre ells. Si l'angle entre els costats és un angle recte, el teorema del cosinus es redueix a l'equació de Pitàgores.
Demostracions[modifica]
Aquest teorema pot arribar a tenir més demostracions conegudes que qualsevol altre (la llei de reciprocitat quadràtica pot ser un altre candidat per a aquesta distinció). El llibre La proposició de Pitàgores conté 370 demostracions.[22]
Per sostracció d'àrees d'un mateix quadrat[modifica]


Suposant el triangle de catets a i b (formant un angle recte) i la hipotenusa c, es tracta de demostrar que l'àrea del quadrat de costat c és igual a la suma de les àrees dels quadrats de costat a i costat b.
Si s'afegeixen tres triangles iguals a l'original al voltant del quadrat de costat c formant la figura mostrada en la imatge, s'obté un quadrat. En efecte, si la figura central de costat c primerament dibuixada és un quadrat, els seus costats formaran angles rectes; llavors, si es gira el triangle original 90 graus al voltant del centre del quadrat, vindrà a ocupar un posició perpendicular a l'original, de mode tal que el costat a serà col·lineal al costat b i viceversa, formant-se un quadrat de costat .
L'àrea d'aquest quadrat pot expressar-se de dues maneres:
- El quadrat del costat:
- Suma del quadrat original i els triangles afegits:
Igualant ambdues expressions:
equació que expressa la igualtat d'àrees dels dos quadrats del dibuix de la dreta. Sostraient de tots dos l'àrea dels quatre triangles resulta:
- , com volíem demostrar.
Demostració atribuïda a Pitàgores[modifica]
Aquesta prova és la traducció, en llenguatge matemàtic actual, de la ideada pel mateix Pitàgores que va emprar la figura següent:
Al voltant del triangle ABC, es construeixen tres quadrats: el roig, d'àrea a², el blau d'àrea b², i el bicolor verd ataronjat, d'àrea c².
- Els triangles rectangles ABC i HBC són semblants (o similars) perquè comparteixen el mateix angle B. Per tant tenim la igualtat dels quocients: BH / BC = BC / BA, és a dir a'/a = a/c (hui en dia, es diria que el seu valor és el sinus de B).
Pel producte creuat: a² = a' · c (és el que es coneix com a teorema del catet), o siga que les àrees roja i ataronjada són iguals.
- De la mateixa manera, a partir dels triangles ABC i HAC i aplicant de nou el teorema del catet, es dedueix que b'/b = b/c (senet A) i després b² = b' · c , o siga que les àrees blaves i verda són iguals.
Sumant les àrees roja i blava, obtenim les àrees ataronjades i verda, és a dir:
Aquesta prova utilitza el teorema de Tales, un cas particular dels triangles semblants, teorema que només és vàlid en els espais euclidians (sense curvatura).
Demostració utilitzant triangles semblants[modifica]

Aquesta demostració es basa en la proporcionalitat dels costats de dos triangles semblants, és a dir, en el fet que la relació de qualsevol dels dos costats corresponents de triangles semblants és el mateix independentment de la grandària dels triangles.
Sigui ABC un triangle rectangle, amb l'angle recte que es troba a C, com es mostra a la figura. Dibuixem l'altura del punt C, i anomenem H la seva intersecció amb el costat AB. El punt H divideix la longitud de la hipotenusa c en les parts d i e. El nou triangle ACH és similar al triangle ABC, perquè tots dos tenen un angle recte (per definició de l'altura), i comparteixen l'angle en A, el que significa que el tercer angle serà el mateix en ambdós triangles, que apareixen marcats com a θ a la figura. Per un raonament semblant, el triangle CBH és també similar a ABC. La prova de la similitud dels triangles requereix el postulat del Triangle: la suma dels angles d'un triangle són dos angles rectangles, i és equivalent al postulat de les paral·leles. La semblança dels triangles porta a la igualtat de les relacions entre els costats corresponents:
El primer resultat es compara el cosinus de cada angle θ i el segon resultat es compara als sinus. Aquestes relacions es poden escriure com a:
Sumant aquestes dues igualtats, obtenim
que, ordenant-ho, tenim el teorema de Pitàgores:
Aquesta és una demostració mètrica en el sentit de Dantzig, que depèn de la longitud i no de l'àrea. El paper d'aquesta demostració en la història és objecte de molta especulació. La qüestió subjacent és la raó per la qual Euclides no va fer ús d'aquesta prova, però en va inventar una altra. Una conjectura és que la demostració de triangles semblants que participen una teoria de les proporcions, no és un tema discutit fins més tard en els elements, i que a la teoria de les proporcions li és necessari un major desenvolupament en aquest moment.[23][24]
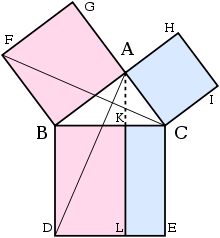
La demostració d'Euclides[modifica]

A grans trets, així és com apareix la demostració sobre el producte als Elements d'Euclides. El gran quadrat es divideix en un rectangle a l'esquerra i a la dreta. Un triangle es construeix en la meitat de l'àrea del rectangle de l'esquerra. A continuació, es construeix un altre triangle que té la meitat de la zona del quadrat a l'esquerra. Aquests dos triangles han de ser congruents, el que demostra que aquest quadrat té la mateixa àrea que el rectangle de l'esquerra. Aquest argument és seguit per una versió similar per al rectangle de la dreta i al quadrat restant. Si es posen els dos rectangles junts per reformar el quadrat de la hipotenusa, la seva àrea és igual a la suma de la superfície dels altres dos quadrats. Els detalls apareixen a la figura del costat.
Siguin A, B, C els vèrtexs d'un triangle rectangle, hi ha un angle recte a A. Generem una perpendicular des de la A fins al costat oposat de la hipotenusa al quadrat de la hipotenusa. Aquesta línia divideix el quadrat de la hipotenusa en dos rectangles, cadascun amb la mateixa superfície que un dels dos quadrats de les potes.
Per a la demostració formal, es requereixen quatre lemes elementals:
- Si dos triangles tenen dos costats de la igualtat a dos costats de l'altra, cadascuna a cada un d'ells, i els angles inclosos pels costats iguals, llavors els triangles són congruents (costat-angle-costat).
- L'àrea d'un triangle és la meitat de la superfície de qualsevol paral·lela en la mateixa base i tenen la mateixa altura.
- L'àrea d'un rectangle és igual al producte de dos costats adjacents.
- L'àrea d'un quadrat és igual al producte de dos dels seus costats (d'acord amb el punt 3).
A continuació, cada quadre superior es relaciona amb un triangle congruent amb un altre triangle relacionat al seu torn a un dels dos rectangles que formen el quadrat inferior.[25]
La demostració és el següent:
- Que ACB és un triangle rectangle amb angle recte CAB.
- En cada un dels costats AC, AB i AC, els quadrats es dibuixen CBDE, BAGF i ACIH, en aquest ordre. La construcció de quadrats requereix els teoremes d'Euclides immediatament anterior, i depèn del postulat de les paral·leles.[26]
- Des d'A, traçar una línia paral·lela a BD i CE. Es tallarà perpendicularment BC i DE en K i L, respectivament.
- Unint CF i AD, per formar el BCF triangles i BDA.
- Els angles CAB i BAG són caironat, de manera que C, A i G estan alineats. De la mateixa manera per a B, A i H.
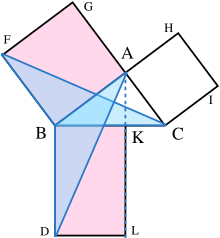
Es mostren els dos triangles congruents de la meitat de l'àrea del rectangle i el quadrat BDLK BAGF. - Els angles CBD i FBA són dos caironat, de manera que l'angle ABD és igual a l'angle FBC, ja que ambdós són la suma d'un angle recte i l'angle ABC.
- Com que AB és igual a FB i BD és igual a BC, el triangle ABD ha de ser congruent amb el triangle FBC.
- Des AKL és una línia recta, paral·lela a BD, llavors BDLK paral té dues vegades l'àrea del triangle ABD, ja que comparteixen el BD base i tenen la mateixa altura BK, és a dir, una línia normal a la seva base comuna, que connecta les línies paral·leles BD i AL. (Lema 2)
- Com que C és colineal amb A i G, el quadrat BAGF ha de ser el doble de la superfície de triangle FBC.
- Per tant BDLK rectangle ha de tenir el mateix lloc que el quadrat BAGF AB2 =.
- De la mateixa manera, es pot demostrar que CKLE rectangle ha de tenir la mateixa àrea que ACIH quadrats AC2 =.
- La incorporació d'aquests dos resultats, AB2 + AC2 = BD × × BK + KL KC
- Ja que BD = KL, BD * BK + KL × KC = BD (BK + KC) x = BD BC
- Per tant AB2 + AC2 = BC2, ja que CBDE és un quadrat.
Aquesta prova, que apareix en els Elements d'Euclides com el de la Proposició 47 en el llibre 1,[27] demostra que l'àrea del quadrat de la hipotenusa és la suma de les superfícies de les altres dues places.[28] Per tant, un mostreig d'àrees la prova en el sentit de Dantzig, que depèn de les zones, no longituds. Això fa que sigui molt diferent de la prova per semblança de triangles, que es conjectura que és la prova que Pitàgores.[24][29]
Demostració de Bhaskara[modifica]

Bhaskara II, el matemàtic i astrònom hindú del segle xii, fa la següent demostració del teorema de Pitàgores.
El teorema es pot demostrar algebraicament amb quatre còpies d'un triangle rectangle amb costats a, b i c, disposades dins d'un quadrat de costat c com en la meitat superior del diagrama.[30] Els triangles són similars amb àrea de , mentre que el petit quadrat té el costat b − a i una àrea de (b − a)². L'àrea del quadrat gran és per tant
Però això és un quadrat amb c laterals i zona C², per la qual cosa
Demostració de Garfield[modifica]

Una prova similar ala de Bhaskara va ser publicada per James A. Garfield.[31][32] En lloc d'un quadrat s'utilitza un trapezi, que pot ser construït a partir de la plaça en la segona de les proves dalt per bisectriu al llarg d'una diagonal de la plaça interior, per donar el trapezi com es mostra en el diagrama. L'àrea del trapezi es pot calcular a la meitat de l'àrea del quadrat, és a dir
La plaça interior és similar a la meitat, i només hi ha dos triangles, perquè aquesta prova que l'anterior excepte per un factor de , que es retira de multiplicar per dos per obtenir el resultat.
Demostració de Leonardo da Vinci[modifica]

Partint del triangle rectangle ABC amb els quadrats de catets i hipotenusa, Leonardo afegeix els triangles ECF i HIJ, iguals al donat, resultant-ne dos polígons, les superfícies dels quals va a demostrar que són equivalents:
- Polígon ADEFGB: la línia DG el divideix en dues meitats idèntiques, ADGB i defg.
- Polígon ACBHIJ: la línia CI determina CBHI i CIJA.
Comparant els polígons destacats en gris, ADGB i CIJA:
- Es veu que tenen tres costats iguals: AD = AC, AB = AJ, BG = BC = IJ
- Així mateix la igualtat entre els angles dels següents vèrtexs:
- A de ADGB i A de CIJA
- B de ADGB i J de CIJA
Es conclou que ADGB i CIJA són iguals.
De manera anàloga es comprova la igualtat entre ADGB i CBHI.
A més, cal notar que un gir de centre A, i sentit positiu, transforma CIJA en ADGB. Mentre que un gir de centre B i sentit negatiu, transforma CBHI en ADGB.
Tot això porta que els polígons ADEFGB i ACBHIJ tenen àrees equivalents. Doncs bé, si a cada un se li trauen els seus dos triangles -iguals - les superfícies que resten forçosament seran iguals. I aquestes superfícies no són sinó els dos quadrats dels catets al polígon ADEFGB, d'una banda, i el quadrat de la hipotenusa al polígon ACBHIJ, per l'altra. El teorema de Pitàgores queda demostrat.
Generalitzacions[modifica]
Cas d'un triangle qualsevol[modifica]

En el cas d'un triangle qualsevol es compleix el teorema del cosinus, i segons la notació del triangle de la imatge adjunta, es compleix que:
Pel cas concret d'un triangle rectangle, l'angle val 90°. Com que el cosinus de 90° val zero, l'últim terme de l'equació s'anul·la i s'obté l'expressió del teorema de Pitàgores.
Així doncs, es pot dir que el teorema de Pitàgores és un cas particular del teorema del cosinus per triangles rectangles.
Amb altres figures formades sobre els costats[modifica]

Euclides diu als Elements:[33]
En els triangles rectangles, la figura construïda a partir del costat que subtendeix l'angle recte és igual a les figures semblants i construïdes de manera semblant a partir dels costats que comprenen l'angle recte.
Aplicant aquesta generalització als semi-discs formats sobre cada costat d'un triangle rectangle, se'n desprèn el teorema de les dues lúnules, segons el qual l'àrea del triangle rectangle és igual a la suma de les àrees de les lúnules dibuixades sobre cada costat de l'angle recte.
El Teorema de Clairaut és una altra generalització, vàlida sobre un triangle qualsevol, sobre els costats dels quals es construeixen paral·lelograms.
En dimensions superiors[modifica]
Es pot concebre la hipotenusa d'un triangle rectangle com la diagonal d'un rectangle, una generalització del teorema en dimensió superior es pot enunciar com segueix:
- En un ortòedre, el quadrat de la gran diagonal és igual a la suma dels quadrats de les dimensions del ortòedre.
Aquest resultat és equivalent al càlcul de la longitud d'un segment a partir de les coordenades cartesianes dels seus extrems en un sistema de coordenades cartesianes:
o en dimensió superior, si té les coordinades i les coordenades :
- .
Aquesta última fórmula també és vàlida en un espai de Hilbert de dimensió infinita i porta a la Identitat de Parseval.
El teorema de de Gua dona una altra generalització del teorema de Pitàgores en un espai euclidià: si un tetràedre té totes les seves arestes ortogonals a un vèrtex llavors el quadrat de l'àrea de la cara oposada al vèrtex és la suma dels quadrats de les àrees de les altres tres cares.
En geometria no euclidiana[modifica]
El teorema de Pitàgores és equivalent a l'axioma de les paral·leles, que es pot redactar així:
|
Això significa que, en els axiomes de la geometria euclidiana, es pot reemplaçar l'«axioma» de les paral·lels pel «teorema» de Pitàgores sense que els altres resultats de la geometria siguin modificats. L'estatus d'axioma i de teorema d'aquests dos resultats són llavors inversos: el «teorema» de Pitàgores esdevé un axioma (una veritat de base, indemostrable, en la qual es recolza la teoria) i l'«axioma» de les paral·lels esdevé un teorema, que pot ser demostrat amb l'ajuda de l'axioma de Pitàgores.
En altres geometries, l'axioma de les paral·leles és reemplaçat per un altre, i el teorema de Pitàgores ja no es compleix.

En geometria esfèrica, si un triangle està format per tres arcs de circumferències màximes a la superfície d'una esfera de radi i si dos d'aquests arcs es creuen en angle recte, la relació del teorema de Pitàgores ja no és vàlida, com en el cas del triangle equilàter trirectangle. S'ha de substituir per la fórmula:
on és la longitud de l'arc oposat a l'angle recte.
Hi ha una relació similar en geometria hiperbòlica per a una curvatura constant igual a −1:
on ch designa la funció cosinus hiperbòlic.
En els dos casos, un desenvolupament limitat d'ordre 2 dona, per a triangles de petita dimensió, la relació del teorema de Pitàgores en geometria plana.
De forma més general, la propietat resisteix malament a ser transferida a altres geometries a causa de la seva curvatura:
- si la curvatura és positiva: ;
- si la curvatura és negativa: ;
- si la curvatura és nul·la: .
En el marc de la relativitat general, l'espai euclidià és reemplaçat per un espai corb on els segments són reemplaçats per geodèsiques.
La teoria de la relativitat general sosté que la matèria i l'energia condueixen l'espai a ser no-euclidià i el teorema no s'aplica doncs estrictament en presència d'energia. Tanmateix, la desviació respecte a l'espai euclidià és feble excepte amb imponents fonts gravitacionals com els forats negres. Determinar si el teorema s'infringeix sobre escales cosmològiques importants, és a dir mesurar la curvatura de l'univers, és un problema obert de la cosmologia.
Altres conceptes relacionats[modifica]
Les ternes pitagòriques són conjunts de tres nombres sencers positius que satisfan el teorema de Pitàgores: la suma dels quadrats dels dos primers és igual al quadrat de l'últim. Exemples de ternes pitagòriques són
La no existència de cap terna per a qualsevol exponent natural més gran que el quadrat, és el Teorema de Fermat.
Les ternes pitagòriques van ser utilitzades profusament pels egipcis en les seves construccions. Els triangles formats amb ternes pitagòriques eren de fàcil construcció, i permetien dibuixar angles rectes només utilitzant nombres naturals. Es per això que als triangles formats per ternes pitagòriques se'ls anomena triangles egipcis.
Referències[modifica]
- ↑ Proposició 47 Arxivat 2011-07-09 a Wayback Machine. del llibre I dels Elements d'Euclides.
- ↑ Proposició 48 Arxivat 2011-07-09 a Wayback Machine. del llibre I dels Elements d'Euclides.
- ↑ Judith D. Sally, Paul Sally. «Chapter 3: Pythagorean triples». A: Roots to research: a vertical development of mathematical problems. American Mathematical Society Bookstore, 2007, p. 63. ISBN 0821844032.
- ↑ George Johnston Allman. Greek Geometry from Thales to Euclid. Reprinted by Kessinger Publishing LLC 2005. Hodges, Figgis, & Co, 1889, p. 26. ISBN 143260662X. «The discovery of the law of three squares, commonly called the "theorem of Pythagoras" is attributed to him by – amongst others – Vitruvius, Diogenes Laertius, Proclus, and Plutarch ...»
- ↑ (Heath 1921, Vol I, p. 144)
- ↑ Otto Neugebauer. The exact sciences in antiquity. Republication of 1957 Brown University Press 2nd. Courier Dover Publications, 1969, p. 36. ISBN 0486223329.. Per a un punt de vista alternatiu vegeu Dick Teresi. Lost Discoveries: The Ancient Roots of Modern Science. Simon and Schuster, 2003, p. 52. ISBN 074324379X., on l'especulació es basa en el fet que en la primera columna de la tauleta 322 de la col·lecció Plimpton es troba el suport al coneixement de Babilònia d'alguns elements de la trigonometria. Aquesta noció és gairebé rebutjada per Eleanor Robson «Words and Pictures: New Light on Plimpton 322». The American Mathematical Monthly. Mathematical Association of America, 109, 2, 2002, pàg. 105–120. DOI: 10.2307/2695324. JSTOR: 2695324. Vegeu també [1] Arxivat 2013-09-21 a Wayback Machine.
 PDF. Sota el coneixement que es té en l'actualitat s'accepta que els babilonis no tenien consciència de les funcions trigonomètriques. Vegeu Abdulrahman A. Abdulaziz (2010), "The Plimpton 322 Tablet and the Babylonian Method of Generating Pythagorean Triples", arΧiv:1004.0025
§2, pàg. 7.
PDF. Sota el coneixement que es té en l'actualitat s'accepta que els babilonis no tenien consciència de les funcions trigonomètriques. Vegeu Abdulrahman A. Abdulaziz (2010), "The Plimpton 322 Tablet and the Babylonian Method of Generating Pythagorean Triples", arΧiv:1004.0025
§2, pàg. 7.
- ↑ Mario Livio. The golden ratio: the story of phi, the world's most astonishing number. Random House, Inc, 2003, p. 25. ISBN 0767908163.
- ↑ Tobias Dantzig. The bequest of the Greeks. Charles Scribner's Sons, 1955, p. 97.
- ↑ (Maor 2007, p. 39)
- ↑ GJ Allman. Thomas Spencer Baynes. The Encyclopaedia Britannica: A Dictionary of Arts, Sciences, and General Literature, Volume 20. 9th. H.G. Allen, 1888, p. 142.
- ↑ Villatoro, Francisco R. «El significado matemático de la tablilla babilónica Plimpton 322». La Ciencia de la Mula Francis. Naukas. [Consulta: 17 setembre 2017].
- ↑ Domínguez, Nuño «Solucionado un enigma matemático de 3.700 años». El País, 25-08-2017 [Consulta: 30 agost 2017].
- ↑ Mansfield, Daniel F. «Plimpton 322: A Study of Rectangles». Foundations of Science, 2021. DOI: 10.1007/s10699-021-09806-0.
- ↑ El matemàtic Bartel van der Waerden [2][Enllaç no actiu] i l'enginyer Alexander Thom [3][Enllaç no actiu] haurien descobert triplets pitagòrics sobre llocs megalítics a la Gran Bretanya i a Carnac, però les seves anàlisis són discutides per Kaveing i Keller [4][Enllaç no actiu]
- ↑ Vegeu el text de Plutarc[Enllaç no actiu] i els treballs de Jean Philippe Lauer relatats a La geometria egípcia [Enllaç no actiu] de Théophile Obenga.
- ↑ André Demailly atribueix ja aquesta competència als agrimensors egipcis en Herbert Simon i les ciències de disseny [Enllaç no actiu]. És fins i tot així com Thomas Henri Martin imagina la difusió d'aquest saber als grecs i als Xinesos en Els signes numerals als pobles de l'Antiguitat i de l'Edat Mitjana[Enllaç no actiu]
- ↑ Chemla, Shuchun, p. 681.
- ↑ La incommensurabilitat del costat i de la diagonal del quadrat es pot tanmateix demostrar sense recórrer al teorema de Pitàgores.
- ↑ Entrada «Irracional» § iii b a (Baruk 1992)
- ↑ (en anglès) Scott E. Brodie. «The Pythagorean Theorem is Equivalent to the Parallel Postulate». Cut-the-Knot.
- ↑ Vegeu Renaixement de la geometria no euclidiana entre 1860 i 1900[Enllaç no actiu], per Jean-Daniel Voelke, pàgina 40 i següents; Gauss declara explícitament que només mesures sobre distàncies «immensament superiors al radi de la Terra» permetrien tal comprovació.
- ↑ (Loomis 1968)
- ↑ (Maor 2007, p. 39) page 39
- ↑ 24,0 24,1 Stephen W. Hawking. God created the integers: the mathematical breakthroughs that changed history. Philadelphia: Running Press Book Publishers, 2005, p. 12. ISBN 0762419229.
- ↑ Vegeu, per exemple, Mike May S.J., Pythagorean theorem by shear mapping Arxivat 2016-10-14 a Wayback Machine., Saint Louis University website Java applet
- ↑ Jan Gullberg. Mathematics: from the birth of numbers. W. W. Norton & Company, 1997, p. 435. ISBN 039304002X.
- ↑ Elements 1.47 by Euclid. Retrieved 19 December 2006.
- ↑ Euclid's Elements, Book I, Proposition 47: web page version using Java applets from Euclid's Elements by Prof. David E. Joyce, Clark University
- ↑ The proof by Pythagoras probably was not a general one, as the theory of proportions was developed only two centuries after Pythagoras; see (Maor 2007, p. 25) page 25
- ↑ Alexander Bogomolny. «Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #3». Cut the Knot. [Consulta: 4 novembre 2010].
- ↑ Published in a weekly mathematics column: James A Garfield The New England Journal of Education, 3, 1876, pàg. 161. as noted in William Dunham. The mathematical universe: An alphabetical journey through the great proofs, problems, and personalities. Wiley, 1997, p. 96. ISBN 0471176613. and in A calendar of mathematical dates: April 1, 1876 Arxivat de juliol 14, 2010, a Wayback Machine. by V. Frederick Rickey
- ↑ Prof. David Lantz' animation Arxivat 2013-08-28 a Wayback Machine. from his web site of animated proofs
- ↑ «Proposició 31 del llibre VI». Arxivat de l'original el 2011-05-14. [Consulta: 18 juny 2011].
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Teorema de Pitàgores |
- Pythagorean Theorem (més de 70 demostracions a cut-the-knot)
- Demostració interactiva en llenguatge Java del Teorema de Pitàgores. Enllaç interactiu











































