Nombre irracional
Un nombre irracional és un nombre real que no és racional,[1] és a dir, que no es pot expressar com una fracció , a la qual a i b són enters, i b és diferent de 0. Els nombres irracionals són precisament aquells l'expansió decimal dels quals no s'atura mai, i tampoc no entra mai en un cicle periòdic. Ja que els nombres reals no són enumerables mentre que els racionals sí (diagonalització de Cantor), gairebé tots els nombres reals són irracionals.
Alguns nombres irracionals són nombres algebraics, com l'arrel quadrada de 2 o l'arrel cúbica de 5; altres són transcendents, com i .
Irracionalitat de certs logaritmes[modifica]
Suposem que el log₂3 sigui racional.
Llavors, per alguns enters positius m i n, tenim .
- En conseqüència, .
- Així, .
- Però 2m és parell (ja que almenys un dels seus factors primers és 2) i 3n és imparell (ja que cap dels seus factors primers és 2; tots són 3). Tenim, doncs, una contradicció, i per tant log₂3 ha de ser irracional.
Nombres irracionals i expansions decimals[modifica]
De vegades se suposa erròniament que els matemàtics defineixen els «nombres irracionals», en termes d'expansions decimals i que declaren que un nombre és irracional si la seva expansió decimal no es repeteix ni acaba. Cap matemàtic pren aquesta definició en consideració, ja que l'elecció de la base 10 és arbitrària i la definició estàndard és molt millor.
De tota manera, és cert que un nombre té la forma n/m on n i m són enters, si i només si la seva expansió decimal es repeteix o acaba. Quan l'algorisme de divisió euclidiana que s'aprèn a l'escola s'aplica a la divisió de n per m, només són possibles m residus. Si el residu és 0, l'expansió decimal s'atura. Si el residu no és 0, l'algorisme només pot córrer m − 1 vegades sense usar un residu més d'un cop. Si un residu es repeteix, l'expansió decimal també!
A la inversa, suposem que trobem una expansió decimal periòdica, per exemple:
A = 0,7162162162...
Com que la longitud del període és 3, multipliquem per 103:
1000A = 716,2162162...
Observem que tant el valor numèric de A com el de 1000A tenen la mateixa cua, el període 162. Per tant, si restem A dels 2 costats de l'última igualtat, la cua s'anul·larà:
999A = 715,5
Llavors
A = 715,5/999 = 7155/9990 = 53/74 (trobant el màxim comú divisor)
53/74 és un quocient d'enters, i per tant un nombre racional.
Nombres que actualment no se sap si són irracionals[modifica]
No se sap si π + e o π − e són irracionals o no. De fet, no existeix un parell de nombres enters m i n pels quals se sàpiga si mπ + ne és o no irracional (vegeu al respecte la conjectura de Schnauel). Tampoc no se sap si 2e, πe, π√2 o la constant γ són irracionals.
El conjunt de tots els nombres irracionals[modifica]
El conjunt de tots els nombres irracionals és no numerable. En usar el valor absolut per a mesurar distàncies, els nombres irracionals són un espai mètric que no és un complet. De tota manera, aquest espai mètric és homeomòrfic a l'espai mètric complet de totes les successions d'enters positius; l'homeomorfisme ve donat per l'expansió infinita en fraccions contínues. Això mostra que el teorema de categories de Baire s'aplica a l'espai de nombres irracionals.
Història[modifica]
Hom ha suggerit que el concepte d'irracionalitat fou acceptat de forma implícita pels matemàtics hindús des del segle vii aC, quan Manava (ca. 750 – 690 AC) creia que les arrels quadrades de nombres com 2 o 61 no es podien determinar de forma exacta.[2] Tot i això, l'historiador Carl Boyer afirma que "...aquestes afirmacions no estan ben fonamentades i és possible que no siguin certes."
| « | (anglès) It has been claimed also that the first recognition of incommensurables appears in India during the Sulbasutra period, but such claims are not well substantiated. The case for early Hindu awareness of incommensurable magnitudes is rendered most unlikely by the lack of evidence that Indian mathematicians of that period had come to grips with fundamental concepts. | (català) S'ha afirmat també que la primera identificació dels incommensurables apareix a l'Índia durant el període Sulbasutra, però aquestes afirmacions no estan ben fonamentades. La idea que els hindús fossin conscients de les magnituds incommensurables es fa encara més improbable per la falta de proves que els matemàtics hindús de l'època s'haguessin familiaritzat amb els conceptes fonamentals. | » |
| — Carl Benjamin Boyer, A History of Mathematics. China and India.[3] | |||
Antiga Grècia[modifica]
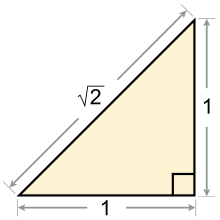
La primera demostració de l'existència dels nombres irracionals s'atribueix usualment a un pitagòric (possiblement Hipàs de Metapont),[4] qui probablement els descobrí mentre identificava les cares del pentacle.[5] El mètode pitagòric de l'època hauria afirmat que existeix una unitat suficientment petita i indivisible que podria encaixar perfectament en una d'aquestes longituds així com en l'altra. Tot i això, Hipàs, al segle v aC, fou capaç de deduir que, de fet, no existia cap unitat de mesura comuna, i que l'afirmació d'aquesta existència era una contradicció. Ho va demostrar tot observant que si la hipotenusa d'un triangle rectangle isòsceles fos commensurable amb un catet, llavors aquesta unitat de mesura hauria de ser alhora parell i senar, la qual cosa és impossible. Es seu raonament és el següent:
- Comencem amb un triangle rectangle isòsceles amb costats enters a, b i c. El quocient de la hipotenusa entre el catet es representa per .
- Assumim que a, b i c estan expressats en els termes més petits possibles (és a dir, no tenen factors comuns).
- Pel teorema de Pitàgores: . (Com que el triangle és isòsceles, ).
- Com que , c² és divisible per 2, i per tant és parell.
- Com que c² és parell, llavors c ha de ser també parell.
- Com que c i b no tenen factors comuns, i c és parell, llavors b ha de ser senar (si b fos parell, b i c tindrien el factor comú 2).
- Com que c és parell, si dividim c per 2 obtenim un enter. Sigui y aquest enter ().
- Si elevem al quadrat totes dues bandes de obtenim o, cosa que és el mateix, .
- Substituint 4y² per c² en la primera equació () obtenim .
- Dividint per 2 tenim .
- Com que y és un enter, i , llavors b² és divisible per 2, i per tant és parell.
- Com que b² és parell, llavors b ha de ser també parell.
- En canvi, hem suposat que b ha de ser senar, i b no pot ser parell i senar alhora. Aquesta contradicció demostra que c i b no poden ser ambdós enters, i així es dedueix que ha d'existir un nombre que no pot ser expressat com a quocient de dos enters.[6]
Els matemàtics grecs anomenaren aquest quocient de magnituds incommensurables alogos, o inexpressables. Hipàs, això no obstant, no va ser elogiat pels seus esforços: segons una llegenda, va fer aquest descobriment mentre s'havia fet a la mar, i fou llençat per la borda pels seus companys pitagòrics «...per haver construït un element en l'univers que negava la [...] doctrina de què tot fenomen de l'univers es pot reduir a nombres enters i llurs quocients.»[7] Una altra llegenda afirma que Hipàs fou exiliat per aquesta revelació. Independentment de les conseqüències personals per Hipàs, aquest descobriment va plantejar un problema seriós per als matemàtics pitagòrics, ja que va fer miques la suposició de què els nombres i la geometria eren inseparables –un fonament de la seva teoria.
El descobriment de ràtios incommensurables era indicatiu d'un altre problema per als grecs: la relació entre el discret i el continu. Aquest problema fou plantejat per primer cop per Zenó d'Elea, que va qüestionar la concepció de què les quantitats són discretes i estan compostes d'un nombre finit d'unitats d'una determinada grandària. Les concepcions anteriors dels grecs dictaven que això era necessàriament així, perquè «els nombres enters representen objectes discrets, i una ràtio commensurable representa una relació entre dues col·leccions d'objectes discrets.»[8] Això no obstant, Zenó va trobar de forma efectiva que «[les quantitats] en general no són col·leccions discretes d'unitats; aquesta és la raó perquè apareixen [quantitats] incommensurables[...] Les quantitats són, en altres paraules, contínues.»[8] El que això significa és que, contràriament a la creença popular de l'època, no pot haver una unitat de mesura mínima i indivisible per qualsevol quantitat, i que, de fet, aquestes divisions de la quantitat han de ser infinites. Per exemple, considerem un segment de recta: aquest segment es pot dividir per la meitat, aquesta meitat es pot dividir per la meitat, i així successivament. Aquest procés pot continuar indefinidament, perquè sempre hi ha una meitat que es pot dividir en 2. Com més vegades dividim el segment, la seva longitud estarà més a prop de zero, però mai no arribarà a zero. Això és exactament el que Zenó volia demostrar. Ho va intentar formulant les seves quatre paradoxes, que demostraven les contradiccions inherents en el pensament matemàtic de l'època. Tot i que les paradoxes de Zenó demostraren de forma precisa les deficiències de les concepcions matemàtiques coetànies, no van ser considerades com a demostració del recíproc. En les ments dels grecs, el fet de refutar la validesa d'una afirmació no demostrava necessàriament la validesa d'una altra, i per tant fou necessària una investigació posterior.
El proper pas fou pres per Èudox de Cnidos, que va formalitzar una nova teoria de la proporció que tingué en compte tant quantitats commensurables com incommensurables. La idea principal era la distinció entre magnitud i nombre. Una magnitud «...no era un nombre, sinó una representació d'entitats com segments de línia, angles, àrees, volums i temps, que podien variar, en el nostre llenguatge, de forma contínua. Les magnituds eren oposades als nombres, que saltaven d'un valor a un altre, com del 4 al 5.»"[9] Els nombres estan compostos d'alguna unitat mínima i indivisible, mentre que les magnituds es poden reduir infinitament. Com que no es podien assignar valors quantitatius a les magnituds, Èudox fou capaç d'identificar ràtios commensurables i incommensurables mitjançant la definició de ràtio en termes de la seva magnitud, i la proporció com una igualtat entre dues ràtios. Tot eliminant els valors quantitatius (els nombres) de l'equació, va poder evitar la trampa d'haver d'expressar un nombre irracional com un nombre. «La teoria d'Èudox va permetre els matemàtics grecs fer progressos notables en geometria, ja que crearen els fonaments lògics necessaris per les ràtios incommensurables.»[10] El llibre 10 està dedicat a la classificació de les magnituds irracionals.
Com a resultat de la distinció entre nombre i magnitud, la geometria esdevingué l'únic mètode que podia considerar les ràtios incommensurables. Com que els fonaments numèrics anteriors encara eren incompatibles amb el concepte d'incommensurabilitat, l'objectiu dels grecs va allunyar-se d'aquestes concepcions numèriques com l'àlgebra, i es traslladà gairebé exclusivament a la geometria. De fet, en molts casos les concepcions algebraiques eren reformulades en termes geomètrics. Podem pensar que hem heretat això fins als nostres dies, ja que entenem x² o x3 com a x al quadrat o x al cub, en comptes de x a la segona potència o x a la tercera potència. També fou crucial per l'obra de Zenó sobre les magnituds incommensurables el fet de centrar-se en el raonament deductiu que resultà de la davallada fundacional dels matemàtics grecs anteriors. El fet que alguns conceptes bàsics de la teoria existent estiguessin en conflicte amb la realitat feia necessària una investigació completa i exhaustiva dels axiomes i suposicions que formaven aquesta teoria. Més enllà d'aquesta necessitat, Èudox desenvolupà el seu mètode d'exhaustió, un tipus de reducció a l'absurd que «...establia l'organització deductiva sobre la base d'axiomes explícits...», així com «...reforçava la decisió anterior de recolzar-se en el raonament deductiu per [confeccionar una] demostració.»[11] Aquest mètode d'exhaustió és el primer pas en la creació del càlcul.
Teodor de Cirene demostrà la irracionalitat de les arrels enèsimes dels nombres enters fins al 17, però es va detenir aquí probablement perquè l'àlgebra que emprava no es podia aplicar a l'arrel quadrada de 17.[12] No va ser fins Èudox que es desenvolupà una teoria de la proporció que tingué en compte tant ràtios racionals com irracionals, la qual cosa serví com a fonament essencial dels nombres irracionals.[13]
Índia[modifica]
Ja durant el període vèdic a l'Índia es tractaven problemes geomètrics i matemàtics sobre nombres irracionals, com ara l'extracció d'arrels quadrades. S'han trobat referències a aquests càlculs en els Samhita, els Brahmana i de forma més notable en els Sulba Sutra (800 aC o abans).[14]
Es creu que Aryabhata (segle v) fou capaç de calcular el valor de π fins a 5 xifres significatives, i que emprà el mot āsanna (aproximat) per referir-se no només al fet que es tractava d'una aproximació, sinó també de què aquest valor és incommensurable (o irracional). Més endavant, en els seus tractats, els matemàtics hindús van escriure sobre l'aritmètica de les arrels enèsimes, incloent l'addició, subtracció, multiplicació, racionalització, i separació i extracció d'arrels quadrades.[15]
Matemàtics com Brahmagupta (el 628) i Bhaskara I (el 629) contribuïren en aquesta àrea, així com altres matemàtics posteriors. En el segle xii, Bhaskara II avaluà algunes d'aquestes fórmules i les va criticar, tot identificant les seves limitacions.
Entre els segles xiv i xvi, Madhava de Sangamagrama i l'Escola de Kerala d'astronomia i matemàtiques van descobrir les sèries infinites per diversos nombres irracionals, com π i certs valors irracionals de funcions trigonomètriques. Jyeṣṭhadeva va proporcionar demostracions per a aquestes sèries infinites al Yuktibhāṣā.[16]
Edat mitjana[modifica]
A l'edat mitjana, el desenvolupament de l'àlgebra per matemàtics islàmics facilità que els nombres irracionals es tractessin com a objectes algebraics.[17] Els matemàtics de l'Orient mitjà també van fusionar els conceptes de nombre i magnitud sota la idea més general de nombre real, van fer crítiques sobre la idea d'Euclides de raó aritmètica, desenvoluparen la teoria de raons compostes, i van estendre el concepte de nombre a les ràtios de magnitud contínua.[18] Al seu comentari sobre el Llibre 10 dels Elements, el matemàtic persa Al-Mahani (d. 874/884) examinà i classificà els irracionals quadràtics i els irracionals cúbics. Treballava amb aquests nombres lliurement, però els explicà de forma geomètrica, de la següent manera:[19]
| « | Serà una (magnitud) racional si, per exemple, diem 10, 12, 3%, 6%, etc., perquè el seu valor es pronuncia i s'expressa quantitativament. Allò que no és racional és irracional i és impossible pronunciar-ho i representar el seu valor quantitativament. Per exemple: les arrels de nombres com 10, 15, 20 que no són quadrats, els costats de nombres que no són cubs, etc. | » |
En contrast amb el concepte euclidià de magnituds com a línies, Al-Mahani considerava els enters i fraccions com a magnituds racionals, i les arrels quadrades i arrels cúbiques com a magnituds irracionals. També introduí una aproximació aritmètica al concepte d'irracionalitat, ja que atribueix el següent a les magnituds irracionals:[19]
| « | les seves sumes o diferències, o els resultats de la seva addició a una magnitud racional, o els resultats de substreure una magnitud d'aquest tipus a una d'irracional, o d'una magnitud racional d'ells. | » |
El matemàtic egipci Abu-Kàmil Xujà (vers 850 – vers 930) fou el primer a acceptar els nombres irracionals com a solucions d'equacions quadràtiques o com a coeficients d'una equació, sovint en la forma d'arrels quadrades, arrels cúbiques i arrels quartes.[20] Al segle x el matemàtic iraquià Al-Hashimi proporcionà demostracions generals (més aviat que demostracions geomètriques) pels nombres irracionals, ja que considerà la multiplicació, la divisió i altres funcions aritmètiques.[21] Abu-Jàfar al-Khazin (900–971) donà una definició de magnituds racionals i irracionals, afirmant que si una quantitat definida és:[22]
| « | continguda en una certa magnitud donada un o més cops, llavors aquesta magnitud (donada) correspon a un nombre racional [...] Cada cop que aquesta (última) magnitud constitueix una meitat, o un terç, o un quart de la magnitud donada (de la unitat), o, comparada (amb la unitat), constitueix tres, cinc, o tres cinquens, és una magnitud racional. I, en general, tota magnitud que correspon a aquesta magnitud (és a dir, a la unitat), de la mateixa manera que un nombre a un altre, és racional. Si, al contrari, una magnitud no es pot representar com un múltiple, una part (1/n), o diverses parts (m/n) d'una certa magnitud, llavors és irracional, és a dir, no es pot expressar de cap altra manera que mitjançant arrels. | » |
Molts d'aquests conceptes foren eventualment acceptats per matemàtics europeus poc després de les traduccions llatines del segle xii. Al-Hassār, un matemàtic marroquí de Fes especialitzat en la jurisprudència d'herència islàmica durant el segle xii, és el primer a mencionar l'ús d'una barra fraccionària, on els numeradors i els denominadors se separen per una barra horitzontal. En la seva discussió, escriu: "..., per exemple, si hom et demana escriure tres cinquens i un terç d'un cinquè, escriu així, ."[23] Aquesta mateixa notació fraccionària apareix poc després en l'obra de Fibonacci en el segle xiii.[24]
Època moderna[modifica]
El segle xvi va veure l'acceptació definitiva per part dels europeus dels nombres enters negatius i no negatius i dels fraccionaris. El segle xvii va veure les fraccions decimals amb la notació moderna força generalment usada pels matemàtics. Però no va ser fins al segle xix que els irracionals no varen ser separats entre algebraics i transcendents, i es va reprendre altre cop un estudi científic de la teoria dels irracionals. Varen romandre gairebé dormint des d'Euclides. L'any 1872 va veure la publicació de les teories de Karl Weierstrass (pel seu alumne Kossak), Heine (Journal de Crelle, 74), Georg Cantor (Mathematische Annalen, 5), i Richard Dedekind. Charles Méray va adoptar el 1869 el mateix punt de partida que Heine, però la teoria és referida habitualment l'any 1872. El mètode de Weierstrass ha estat completament desenvolupat per Salvatore Pincherle (1880),[25] i el de Dedekind ha agafat rellevància addicional a través del treball posterior de l'autor (1888) la confirmació recent de Paul Tannery (1894). Weierstrass, Cantor, i Heine basen les seves teories en sèries infinites, mentre Dedekind fonamenta les seves en la idea d'una partició (Schnitt) en el sistema de nombres reals, separen tots els nombres racionals en dos grups que tenen certes propietats característiques. La matèria ha rebut contribucions posteriors a les mans de Weierstrass, Kronecker (Journal de Crelle, 101), i Méray.
Les fraccions contínues, estretament relacionades amb els nombres irracionals, varen rebre atenció a les mans d'Euler, i al començament del segle xix varen agafar importància a través dels escrits de Joseph Louis Lagrange. Altres contribucions dignes d'esment han estat fetes per Druckenmüller (1837), Kunze (1857), Lemke (1870), i Günther (1872). Ramus (1855) és el primer que va connectar la matèria amb els determinants, resultant-ne les subsegüents contribucions de Heine, Möbius, i Günther, en la teoria de Kettenbruchdeterminanten. Dirichlet també va fer aportacions a la teoria general, així com nombroses contribucions a la seva aplicació.
Johann Heinrich Lambert demostrà el 1761 que π no pot ser racional, i que en és irracional si n és racional (llevat que n = 0).[26] Encara que s'acostuma a considerar que la demostració de Lambert és incompleta, algunes avaluacions modernes la consideren satisfactòria, i de fet per la seva època és inusualment rigorosa. Adrien-Marie Legendre (1794), després d'introduir la funció de Bessel–Clifford, va proporcionar una demostració de què π² és irracional, d'on es desprèn immediatament que π també és irracional. L'existència de nombres transcendents va ser establerta per primer cop per Joseph Liouville (1844, 1851). Més endavant, Georg Cantor (1873) va demostrar la seva existència mitjançant un mètode diferent. Charles Hermite (1873) va ser el primer a demostrar que e és transcendent, i Ferdinand von Lindemann (1882), a partir de les conclusions d'Hermite, va demostrar el mateix per a π. Weierstrass (1885) va simplificar notablement la demostració de Lindemann, posteriorment David Hilbert (1893) la va simplificar encara més, i finalment Adolf Hurwitz i Paul Gordan van fer-ne una demostració elemental.
Referències[modifica]
- ↑ «Nombre irracional». Gran Enciclopèdia Catalana. Barcelona: Grup Enciclopèdia Catalana.
- ↑ T. K. Puttaswamy, "The Accomplishments of Ancient Indian Mathematicians", pp. 411–2, a D'Ambrosio, editors, Helaine Selin, advisory editor, Ubiratan. Mathematics across cultures : the history of non-Western mathematics. Digital pr.. Dordrecht: Kluwer., 2001. ISBN 1-4020-0260-2.
- ↑ Boyer, Carl B. «China and India». A: A history of mathematics. 1a ed.. Princeton, N.J.: Princeton University Press, 1985, p. 208. ISBN 9780691023915.
- ↑ Von Fritz, Kurt «The Discovery of Incommensurability by Hippasus of Metapontum». The Annals of Mathematics, 1945.
- ↑ Choike, James R. «The Pentagram and the Discovery of an Irrational Number». The Two-Year College Mathematics Journal, 1980.
- ↑ Kline, Morris. Mathematical thought from ancient to modern times (en anglès). Paperback edition.. Nova York: Oxford University Press, 1990, p. 33. ISBN 978-0195061352.
- ↑ Kline 1990, p. 32.
- ↑ 8,0 8,1 Kline 1990, p.34.
- ↑ Kline 1990, p.48.
- ↑ Kline 1990, p.49.
- ↑ Kline 1990, p.50.
- ↑ McCabe, Robert L. «Theodorus' Irrationality Proofs». Mathematics Magazine, 1976.
- ↑ Edwards, Charles H. The historical development of the calculus. 3a ed.. Nova York [u.a.]: Springer, 1994. ISBN 978-0-387-94313-8 [Consulta: 21 setembre 2013].
- ↑ Bag, Amulya Kumar «Ritual geometry in India and its parallelism in other cultural areas» (pdf) (en anglès). Indian Journal of History of Science, 25, 07-04-1990. Arxivat de l'original el 25 de setembre 2013 [Consulta: 21 setembre 2013].
- ↑ Datta, Bibhutibhusan; Singh, Avadhesh Narayan «Use of series in India». Indian Journal of History of Science, 28, 1993.
- ↑ Katz, V. J. (1995), "Ideas of Calculus in Islam and India", Mathematics Magazine (Mathematical Association of America) 68 (3): 163–74.
- ↑ O'Connor, John J.; Robertson, Edmund F. «Arabic mathematics: forgotten brilliance?» (en anglès). MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland.
- ↑ Matvievskaya, Galina «The Theory of Quadratic Irrationals in Medieval Oriental Mathematics». Annals of the New York Academy of Sciences, 500, 1 From Deferent, 01-06-1987, pàg. 253–277 [254]. DOI: 10.1111/j.1749-6632.1987.tb37206.x.
- ↑ 19,0 19,1 Matvievskaya, Galina «The Theory of Quadratic Irrationals in Medieval Oriental Mathematics». Annals of the New York Academy of Sciences, 500, 1 From Deferent, 01-06-1987, pàg. 253–277 [259]. DOI: 10.1111/j.1749-6632.1987.tb37206.x.
- ↑ Jacques Sesiano, "Islamic mathematics", p. 148, a D'Ambrosio, editors, Helaine Selin, advisory editor, Ubiratan. Mathematics across cultures : the history of non-Western mathematics. Digital pr.. Dordrecht: Kluwer., 2001. ISBN 1-4020-0260-2.
- ↑ Matvievskaya, Galina «The Theory of Quadratic Irrationals in Medieval Oriental Mathematics». Annals of the New York Academy of Sciences, 500, 1 From Deferent, 01-06-1987, pàg. 253–277 [260]. DOI: 10.1111/j.1749-6632.1987.tb37206.x.
- ↑ Matvievskaya, Galina «The Theory of Quadratic Irrationals in Medieval Oriental Mathematics». Annals of the New York Academy of Sciences, 500, 1 From Deferent, 01-06-1987, pàg. 253–277 [261]. DOI: 10.1111/j.1749-6632.1987.tb37206.x.
- ↑ Cajori, Florian. A history of mathematical notations. [Facsim. ed.].. Nova York: Dover Publications, 1993, p. 269. ISBN 978-0486677668 [Consulta: 21 setembre 2013].
- ↑ (Cajori 1928, pg.89)
- ↑ Pincherle, Salvatore «Saggio di una introduzione alla teorica delle funzioni analitiche secondo i principi del prof. Weierstrass». Giornale di Matematiche, 1880.
- ↑ Lambert, Johann H. «Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques». Histoire de l'Académie Royale des Sciences et des Belles-Lettres der Berlin, 1761, pàg. 265-276.
Vegeu també[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Nombre irracional |


















