Nombre primer
Un nombre primer és un nombre enter superior a 1 que admet exactament dos divisors: 1 i ell mateix.[1][2] Els nombres primers menors que 100 són:
Noteu el fet que tots els nombres naturals són divisibles entre ells mateixos i entre la unitat. Però els que no són primers, a més, també són divisibles entre altres nombres.
El nombre primer més petit és el 2 i, de fet, és l'únic nombre primer que és també parell, ja que qualsevol parell més gran és múltiple de dos.
El teorema fonamental de l'aritmètica estableix que qualsevol enter positiu superior a 1 pot representar-se sempre com un producte de nombres primers, i aquesta representació (factorització) és única. El teorema d'Euclides prova que existeixen infinits nombres primers. A més se sap que no hi ha límit per a la distància entre dos primers consecutius, això és, donat un nombre N, es poden trobar dos nombres primers a i b tals que entre a i b no hi ha altres nombres primers i que la diferència entre a i b és superior a N.
Encara no s'ha pogut provar, però es conjectura, que existeixen infinits nombres primers de la forma p1 = p₂ + 2 (sent p1 i p₂ primers) o primers bessons. Sí que s'ha provat que els únics primers trigèmins (primers de la forma p1 = p₂ + 2 i p₂ = p₃ + 2) són 3, 5 i 7.
Hi ha nombrosos algorismes per trobar nombres primers. El més senzill seria provar de dividir cada nombre per tots els inferiors o iguals a la seva arrel quadrada, però és molt poc eficient perquè requereix moltes divisions innecessàries; per exemple, un cop provat el dos, no cal provar tots els nombres parells, que sabem que seran divisibles per dos. Una extensió d'aquesta idea és el sedàs d'Eratòstenes.
A desembre de 2020, el nombre primer més gran conegut és un primer de Mersenne amb 24.862.048 dígits decimals.
Història[modifica]
L'os d'Ishango, data de fa més de 20.000 anys (abans de l'aparició de l'escriptura). El va trobar l'arqueòleg Jean de Heinzelin de Braucourt.[3] Presenta unes osques que semblen representar quatre nombres primers: 11, 13, 17 i 19. Alguns arqueòlegs interpreten aquest fet com una prova que qui les va fer coneixia els nombres primers. Amb tot, existeixen molt poques troballes que permetin entendre els coneixements que tenia realment l'home d'aquella època.[4]
Nombroses tauletes d'argila seca atribuïdes a les civilitzacions que es van anar succeint a Mesopotàmia al llarg del II mil·lenni a.C. mostren la resolució de problemes aritmètics i acrediten els coneixements de l'època. Per calcular divisions necessitaven conèixer l'invers dels naturals, s'han trobat tauletes amb aquestes taules d'inversos. En el sistema sexagesimal que empraven els babilonis per escriure els nombres, els inversos dels divisors de potències de 60 es calculen fàcilment, per exemple, dividir entre 24 equival a multiplicar per 150 () i desplaçar la coma sexagesimal dos llocs (ja que ). Per conèixer-ho calia una sòlida comprensió de la multiplicació, la divisió i la factorització dels enters.
En les matemàtiques egípcies, el càlcul de fraccions requeria coneixements sobre les operacions, la divisió de naturals i la factorització. Els egipcis només operaven amb les anomenades fraccions unitàries, és a dir, les que tenien numerador igual a 1 (. Les fraccions de numerador diferent d'1 s'escrivien com a suma d'inversos de naturals, si podia ser sense repetició ( en comptes de . Per a això segurament calia tenir una taula dels primers nombres primers.
La primera prova indiscutible del coneixement dels nombres primers es remunta al voltant de l'any 300 aC i es troba en els Elements d'Euclides (volums VII a IX). Euclides defineix els nombres primers, demostra que n'hi ha infinits, defineix el màxim comú divisor i el mínim comú múltiple i proporciona els algorismes per determinar-los que avui es coneixen com a algorisme d'Euclides. Els Elements contenen també el teorema fonamental de l'aritmètica i la manera de construir un nombre perfecte a partir d'un nombre primer de Mersenne.
El garbell o sedàs d'Eratòstenes, atribuït a Eratòstenes de Cirene, és un mètode senzill que permet trobar nombres primers.

Després de l'època de la Grècia antiga, no hi va haver gaires avenços en l'estudi dels nombres primers fins al segle xvii. El 1640 Pierre de Fermat va enunciar sense demostrar-lo el petit teorema de Fermat, més endavant el van demostrar Leibniz i Euler. Pot ser que molt abans ja es coneguera un cas especial d'aquest teorema a la Xina.,[5]
Fermat va enunciar la conjectura de què tots els nombres de la forma són primers (per això aquests nombres s'anomenen nombres de Fermat) i va verificar la hipòtesi fins a n = 4 (és a dir, 2¹⁶ + 1). Però Euler va demostrar que el següent nombre de Fermat (2³² + 1) és compost (un dels seus factors primers és 641). De fet, fins avui no s'ha trobat cap altre nombre primer de Fermat a banda dels que ja coneixia Fermat.
El monjo francès Marin Mersenne va investigar els nombres primers de la forma 2p − 1, amb p primer. En honor seu, avui s'anomenen nombres de Mersenne.
Els treballs d'Euler en teoria de nombres contenen molts resultats referents als nombres primers. Va demostrar que la sèrie infinita (la suma dels inversos dels nombres primers) és divergent. El 1747 va demostrar que tots els nombres perfectes parells són de la forma , on el segon factor és un nombre primer de Mersenne.
A començaments del segle xix, Legendre i Gauss van conjecturar de forma independent que, quan tendeix a infinit, la quantitat de nombres primers menors o iguals que tendeixen asimptòticament a , on és el logaritme natural de . Les idees que Riemann va expressar en un treball de 1859 sobre la funció zeta van obrir un camí que conduiria a la demostració del teorema dels nombres primers. Hadamard i De la Vallée-Poussin, cada un per separat, van donar forma a aquest esquema i van aconseguir demostrar el teorema el 1896.
Actualment, en el cas de nombres grans, per comprovar si un nombre és primer, no es fa per divisions successives. Molts matemàtics han desenvolupat tests de primalitat, sovint restringits a categories específiques de nombres primers. Alguns exemples són el test de Pépin per als nombres de Fermat (1877), el teorema de Proth (~1878), la prova de Lucas-Lehmer per a nombres de Mersenne (a partir de 1856)[6] i el test de Lucas-Lehmer generalitzat. També existeixen algorismes per a nombres arbitraris (és a dir, sense necessitat que pertanyin a una determinada categoria), però són molt més lents, com és el cas del test APRT-cl, el test de primalitat per corbes el·líptiques i el AKS.
Durant molt de temps, es pensava que l'aplicació dels nombres primers era molt limitada fora de la matemàtica pura. Això va canviar en els anys 1970 amb el desenvolupament de la criptografia de clau pública, en la que els nombres primers eren la base dels primers algorismes com l'algorisme RSA.
Des del 1951, el nombre primer més gran conegut sempre ha estat descobert amb l'ajuda d'ordinadors. La recerca de nombres primers cada vegada més grans ha suscitat interès fins i tot fora de la comunitat matemàtica. En els últims anys han guanyat popularitat projectes de computació distribuïda tals com el GIMPS.
Definició[modifica]
Un nombre primer és un nombre natural que té dos i només dos divisors naturals diferents, l'1 i ell mateix.
Fins al segle xix, els matemàtics majoritàriament consideraven que l'1 era primer, entenent-se que la definició de nombre primer consistia en la divisibilitat entre 1 i ell mateix però que no requeria un nombre mínim de divisors diferents. Molts treballs matemàtics continuen sent vàlids malgrat considerar l'1 com un nombre primer, per exemple el treball de Stern i Zeisel. La llista de Derrick Norman Lehmer de nombres primers fins al 10.006.721, reimpresa fins a l'any 1956[7] començava amb l'1 com a primer nombre primer.[8] El canvi de nomenclatura es va produir perquè que fos vàlid el següent enunciat del teorema fonamental de l'aritmètica: «tot nombre natural té una representació única com a producte de factors primers, llevat de l'ordre».[9][10] A més, els nombres primers tenen moltes propietats que no té l'1, tals com la relació del nombre amb el valor corresponent de la funció d'Euler o la funció suma de divisors.[11]
Demostració de la infinitud dels nombres primers[modifica]
La primera demostració de la infinitud dels nombres primers la proporcionà Euclides al llibre IX dels Elements. En la matemàtica moderna, sovint s'ha distorsionat la demostració i s'ha considerat un exemple clàssic de demostració indirecta (no constructiva), però la demostració original és constructiva. Euclides no diu explícitament que existeixen infinits nombres primers, l'enunciat que demostra és que «els nombres primers són més que qualsevol quantitat donada de nombres primers» i la demostració consisteix a construir un nombre primer que no és cap dels donats.[12]
La demostració dels Elements comença amb una quantitat finita donada de nombres primers. Es construeix m el mínim comú múltiple d'aquests primers, i es considera el nombre m + 1. Aquest nombre pot ser primer o no ser-ho. Si ho és, aleshores ja s'ha trobat un primer més dels que hi havia al començament. Si no ho és, aleshores ha de tenir com a divisor un nombre primer. Aquest primer no és cap dels nombres primers amb què s'havia començat, ja que si ho fos aleshores seria divisor tant de m com de m + 1, i en conseqüència seria divisor d'1, la qual cosa és absurda. Així doncs, també en aquest cas s'ha trobat un primer diferent dels del començament. Per tant, la demostració conclou, «els nombres primers són més que qualsevol quantitat donada de nombres primers».
L'enunciat modern, que «existeixen infinits nombres primers», s'ha de demostrar indirectament, per reducció a l'absurd. S'ha de suposar que el conjunt de tots els nombres primers és finit, i arribar a una contradicció. A part d'aquesta subtilesa, la idea de la demostració d'Euclides és vàlida, tot i que se sol substituir el concepte de mínim comú múltiple pel de producte, que en el cas de nombres primers és equivalent.
Per començar la demostració, suposem que el conjunt de nombres primers és finit, i que d'aquests primers P és el més gran. Construïm llavors el nombre (2·3·5·7·11·...·P) + 1, és a dir el producte de tots els nombres primers més u. Aquest nombre no és divisible per 2, ni per 3, ni per 5, ni, en definitiva, per cap nombre primer, ja que en tots els casos la divisió dona 1 com a resta. Per tant només pot ser que (2·3·5·7·11·...·P) + 1 sigui primer o que sigui divisible per un altre nombre primer que està entre P i (2·3·5·7·11·...·P) + 1; en qualsevol dels dos casos hem trobat un nombre primer més gran que P, contradient la suposició inicial i, per tant, demostrant el teorema.
Propietats[modifica]
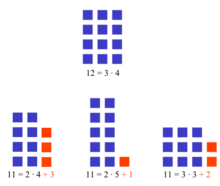
- 2 és l'únic nombre primer parell, atès que qualsevol altre nombre parell més gran de dos és divisible entre 2. Per tant, l'expressió nombre primer senar, vol dir nombre primer més gran que 2.
- Tots els nombres primers excepte 2 i 5, escrits en base 10, acaben en 1, 3, 7 o 9, ja que els que acaben en 0, 2, 4, 6 o 8 són múltiples de 2 i els que acaben en 0 o 5 són múltiples de 5. En general en qualsevol base tots els nombres primers tret d'un nombre finit acaben amb una xifra que és un nombre coprimer amb la base.
- Tots els nombres primers més grans de 3 són de la forma 6n - 1 o 6n + 1, perquè tots els altres nombres són divisibles entre 2 o 3.
- Generalitzant això, tots els nombres primers més grans que q són de forma q#·n + m , on 0 < m < q, i m no té cap factor primer ≤q. (q# o primporial de q és el producte de tots els nombres primers més petits o iguals que q).
- Si p és un nombre primer i p és un divisor de ab, llavors p és un divisor de a o p és un divisor de b (o de tots dos). Aquesta afirmació es coneix amb el nom de lema d'Euclides i es fa servir per demostrar la unicitat de la descomposició en factors primers.
- L'anell Z/nZ és un cos si i només si n és primer. Equivalentment: n és primer si i nomé si φ(n) = n − 1.
- Si p és un nombre primer diferent de 2 i 5, és sempre un nombre decimal periòdic, de període p − 1 o un divisor de p − 1. Això es dedueix directament a partir del petit teorema de Fermat. expressat en base q (en comptes de base 10) s'obtenen propietats similars, sempre que p no sigui un factor primer de q.
- La característica de qualsevol cos és, o bé zero, o bé un nombre primer.
- La constant de Copeland-Erdős 0,235711131719232931374143…, obtinguda per concatenació dels nombres primers consecutius expressats en base 10, és un nombre irracional.
Teoremes relatius als nombres primers[modifica]
Teorema fonamental de l'aritmètica[modifica]
El teorema fonamental de l'aritmètica afirma que
| Tot nombre natural superior a 1 es pot escriure, de forma única com a producte de nombres primers. |
El teorema conté dues afirmacions, la primera és que tot nombre es pot escriure com a producte de nombres primers (això és trivial perquè si no, ell mateix és un nombre primer i per tant compleix l'afirmació com a producte trivial d'un únic factor), la segona és la més interessant i consisteix en el fet que no es poden trobar dos productes diferents (tret de l'ordre en què es presentin els factors). La seva demostració és immediata a partir del lema d'Euclides que diu que: si un nombre primer p és divisor del producte a * b i no és divisor de a llavors és divisor de b.
Teorema de Tchebychev[modifica]
El postulat de Bertrand, anomenat també teorema de Tchebychev, afirma que si n és un nombre natural superior o igual a 1, llavors sempre existeix pel capbaix un nombre primer p tal que
James Joseph Sylvester el va generalitzar amb la proposició següent: el producte de k enters consecutius superiors a k és divisible per un nombre primer més gran que k.
Petit teorema de Fermat[modifica]
El Petit Teorema de Fermat, obtingut per Pierre de Fermat, afirma que si p és un nombre primer, per qualsevol nombre natural a es compleix que .
En el cas que es conegui un nombre a per al qual no es compleixi l'afirmació del teorema, aquest teorema permet afirmar que un nombre no és un nombre primer sense necessitat de conèixer la seva descomposició en factors primers. Aquesta observació es fa servir en alguns tests de primalitat per augmentar la probabilitat que un nombres sigui primer (o garantir que no ho és) a base d'anar provant diferents nombres a escollits a l'atzar.
Els nombres de Carmichael també compleixen la condició imposada pel teorema sense ser nombres primers.
Teorema de Wilson[modifica]
El teorema de Wilson estableix que, el nombre natural p és primer si i només si,
això és, si i només si, és divisible entre p.
Teorema de la progressió aritmètica[modifica]
El teorema de la progressió aritmètica, s'enuncia de la manera següent:
|
Classes de nombres primers[modifica]
Nombres primers de Mersenne[modifica]
Un nombre primer de Mersenne és un nombre primer que és igual a una potència de 2 menys 1. Per exemple, 3 = 4 − 1 = 2² − 1 és un primer de Mersenne, igual que 7 = 8 − 1 = 23 − 1. En canvi, 15 = 16 − 1 = 24 − 1, per exemple, no és primer.
En general, doncs, els nombres primers de Mersenne són nombres primers de la forma:
- Mn = 2n − 1.
Els nombres primers més grans que es coneixen són generalment d'aquesta forma, ja que existeix un test de primalitat molt eficaç, el test de Lucas-Lehmer, per determinar si un nombre de Mersenne és primer o no.
El 2008 el nombre primer més gran conegut era M43.112.609 = 243.112.609 -1, que té 12.978.189 xifres en escriure'l en base deu. Es tracta cronològicament del 45è nombre primer de Mersenne conegut i el seu descobriment es va anunciar el 23 d'agost de 2008 gràcies al projecte de computació distribuïda «Great Internet Mersenne Prime Search» (GIMPS). El 46è nombre primer de Mersenne va ser descobert dues setmanes després, però és més petit que el 45è. El desembre de 2018[13] es va descobrir M82589933 = 282589933 -1, amb 24862048 xifres.
Actualment no se sap si hi ha un nombre infinit de nombres primers de Mersenne, però es té la sospita que la resposta és afirmativa i, de fet, és una part del contingut de la conjectura de Lenstra-Pomerance-Wagstaff.
Nombres primers de Sophie Germain[modifica]
Un nombre primer de Sophie Germain és aquell nombre primer p tal que 2p + 1 també és primer.
Actualment[14] el nombre primer de Sophie Germain més gran que es coneix és 48.047.305.725·2172403 − 1, un nombre de 51910 dígits obtingut el gener de 2007.[15] No se sap si hi ha infinits nombres primers de Germain.
Una successió de nombres , tots ells primers, tals que per a tot , s'anomena cadena (completa) de Cunningham de primera espècie, i compleix per definició que cada un dels seus termes, llevat de l'últim, és un nombre primer de Sophie Germain. Es creu que per a tot n natural existeixen infinites cadenes de Cunningham de longitud n, encara que no es coneix cap mètode directe per generar les esmentades cadenes.
Nombres primers bessons[modifica]
Els nombres primers bessons són aquelles parelles de nombres primers que difereixen en 2. És a dir, p i q (amb p < q) són primers bessons si q = p + 2. Excepte pel cas del 2 i el 3, aquesta és la mínima diferència que pot haver-hi entre dos primers.
No se sap si existeixen infinits nombres primers bessons.
S'ha demostrat que la parella n, n +2 són nombres primers bessons si i només si:
Els nombres primers bessons més grans coneguts són la parella 2003663613 · 2195000 -1 i 2003663613 · 2195000 +1, que té 58711 dígits.[16] Foren descoberts el 2007 per Vautier, McKibbon, Gribenko et al.
Abans eren, la parella 100314512544015 · 2171960 -1 i 100314512544015 · 2171960 +1, que té 51.780 dígits[17] i va ser descobert en el 2006 pels matemàtics hongaresos: Zoltán Járai, Gabor Farkas, Timea Csajbok, Janos Kasza i Antal Járai.
Nombres primers de Fermat[modifica]
Un nombre de Fermat, és un nombre natural de la forma:
on n és natural. Els nombres primers de Fermat són nombres de Fermat que a la vegada són primers.
Es pot demostrar que qualsevol nombre primer de la forma 2n + 1 ha de ser un nombre de Fermat. Els únics nombres primers de Fermat coneguts són F0, F1, F2, F3, i F4.
Conjectures sobre els nombres primers[modifica]
Hi ha moltes qüestions obertes relatives als nombres primers, per exemple:
- La conjectura de Goldbach: Tot nombre natural parell igual o superior a 4 es pot escriure com a suma de dos nombres primers.
- La conjectura de De Polignac: tot nombre natural parell es pot escriure com a diferència de dos nombres primers consecutius i a més hi ha un nombre infinit de maneres.
- Conjectura dels nombres primers bessons: Hi ha una infinitat de nombres primers bessons.
- Tota successió de Fibonacci conté infinits nombres primers.
- Hi ha infinits nombres primers de Fermat.
- Hi ha infinits nombres primers de la forma n² + 1
- La conjectura de Legendre afirma que sempre existeix un nombre primer entre n² i (n+1)². Aquesta conjectura no demostrada està relacionada amb la hipòtesi de Riemann que tampoc està demostrada.
Obtenció de nombres primers[modifica]
Hi ha una sèrie de problemes relacionats amb l'obtenció de nombres primers. Tot i ser diferents, estan íntimament relacionats entre ells:
- Trobar tots els nombres primers més petits que un de donat.
- Donat un nombre, saber si és o no un nombre primer.
- Trobar un nombre primer més gran que un de donat o més gran que un de donat i més petit que un altre.
- Donat un nombre compost, trobar-ne un factor.
- Donat un nombre trobar la seva descomposició en factors primers.
Per resoldre el problema 1 cal saber si cada un dels nombres és o no primer, és a dir resoldre el problema 2 per cada cas. Un algorisme que resol aquest problema és el garbell d'Eratòstenes.
Una forma de resoldre el problema 2 és provar si és divisible o no entre tots els nombres més petits que la seva arrel quadrada. Per fer això hi ha algorismes que fan servir una llista de tots els nombres primers més petits que un de donat (solució del problema 1). De vegades no cal saber amb absoluta certesa si un nombre és primer o no, per algunes aplicacions pràctiques n'hi ha prou amb tenir una probabilitat molt gran de què ho sigui. Els tests de primalitat busquen saber si un nombre no és primer amb certesa i si ho és tenir-ne una probabvilitat molt gran. A l'extrem, quan la probabilitat és del 100% (llavors són demostracions de primalitat) resolen exactament el problema 2.
El problema 3 és de gran interès en criptografia. Una forma de fer-ho és triar un nombre a l'atzar dins de l'interval, aplicar-li un test de primalitat i si falla provar-ne un altre fins que se'n troba un. Encara que sembli poc pràctic aquest mètode funciona força bé perquè hi ha força nombres primers i encara que es tracti de nombres molt grans la quantitat de proves que cal fer és acceptable. Una altra forma seria tenir fórmules que donessin nombres primers.
Els problemes 4 i 5 són pràcticament el mateix. Aplicant repetidament un mètode per resoldre el problema 4 es resol el 5. Això ho fan els algorismes de factorització. Fixeu-vos que tot algorisme de factorització, si falla, és una demostració de primalitat.

Garbell d'Eratòstenes[modifica]
El garbell d'Eratòstenes és una manera senzilla de trobar tots els nombres primers menors o iguals que un nombre donat. Es basa a escriure una llista de tots els nombres naturals des del 2 fins al nombre i ratllar repetidament els múltiples dels nombres primers ja descoberts. El garbell d'Atkin, més modern, té una major complexitat, però si s'optimitza apropiadament també és més ràpid.
Test de primalitat[modifica]
Un mètode per determinar la primalitat d'un nombre és la factorització per prova de divisions, que consisteix a dividir successivament aquest nombre entre els nombres primers menors o iguals a la seva arrel quadrada. Si alguna de les divisions és exacta, llavors el nombre no és primer; en cas contrari, és primer. Per exemple, donat menor o igual que 120, per determinar si és primer n'hi ha prou amb comprovar si és divisible entre 2, 3, 5 i 7, ja que el següent nombre primer, 11, ja és més gran que . És el test de primalitat més senzill. Si el nombre no té factors petits l'algorisme no és pràctic. Per regla general es fa servir aquest procediment només per trobar factors fins a un cert límit, llavors es parla de prova de divisions incompleta.
De totes maneres, és una pas previ per a molts altres tests de primalitat, i si es tracta de nombres triats a l'atzar permet descartar-ne molts amb molt poc temps de càlcul. Per a un n aleatori, existeix un 50% d'oportunitats de què 2 sigui un factor de n, i 33% d'oportunitats de què 3 sigui un factor, i així successivament. Es pot demostrar que un 88% de tots els naturals tenen un factor inferior a 100, i que un 91% tenen un factor inferior a 1000. Per aplicacions de criptografia no és aplicable aquest mètode per factoritzar nombres perquè el nombres compostos que es fan servir ja es trien de manera que els seus factors siguin grans.
Un exemple de funció senzilla en C++ per implementar la prova de divisions és el següent
bool es_primer(int n) {
if (n <= 1) return false;
for (int i = 2; i*i <= n; ++i){
if (n % i == 0) return false;
}
return true;
}
Hi ha molts altres tests de primalitat determinístics que es basen en propietats que caracteritzen els nombres primers, però la seva utilitat computacional depèn molt del test emprat. Per exemple, es podria emprar el teorema de Wilson per calcular la primalitat d'un nombre, però té l'inconvenient de requerir el càlcul d'un factorial, una operació computacionalment prohibitiva quan es manegen nombres grans. Aquí entra en joc el temps d'execució de l'algorisme emprat, que s'expressa en la notació de Landau. Per poder determinar la primalitat de nombres cada vegada més grans (de milers de xifres) es busquen algorismes tals que el seu temps d'execució creixi el més lentament possible, si és possible, que es pugui expressar com un temps polinòmic. Un dels tests determinístics més ràpids és el test de primalitat AKS.
Sovint n'hi ha prou amb tenir una resposta més ràpida amb una alta probabilitat (encara que no segura) de ser certa. Es pot comprovar ràpidament la primalitat d'un nombre relativament gran mitjançant tests de primalitat probabilístics. Aquests tests solen agafar un nombre aleatori anomenat "testimoni" i introduir-lo en una fórmula conjuntament amb el nombre potencialment primer n. Després de diverses iteracions, es resol que n és "amb certesa compost" o bé "probablement primer". Alguns d'aquests tests no són perfectes: hi pot haver nombres compostos que el test consideri "probablement primers" independentment del testimoni emprat. Aquests nombres reben el nom de pseudoprimers per a aquest test. Per exemple, els nombres de Carmichael són nombres compostos, però el test de Fermat els avalua com probablement primers. Tanmateix, els tests probabilístics més emprats, com el test de Miller-Rabin o el test de Solovay-Strassen, no tenen aquest inconvenient.
Alguns tests probabilístics podrien ser deterministes i altres poden millorar el temps d'execució si es compleixen algunes hipòtesis matemàtiques. Per exemple, si es confirmés la hipòtesi generalitzada de Riemann, es pot emprar una versió determinista del test de Miller-Rabin, i el test de primalitat per corbes el·líptiques podria millorar notablement el temps d'execució si es confirmessin algunes hipòtesis de teoria analítica de nombres.
Fórmules que generen nombres primers[modifica]
Al llarg de la història, s'han buscat nombroses fórmules per generar els nombres primers. El nivell més alt d'exigència seria que la fórmula associés a cada nombre natural n l'n-èsim nombre primer. De forma més indulgent, es pot demanar una funció f que associï a cada nombre natural n un nombre primer de tal manera que cada un dels valors obtinguts només aparegui una vegada.
A més, es desitja que la funció es pugui calcular en la práctica.[18] Per exemple, el teorema de Wilson assegura que p és un nombre primer si i només si . Un altre exemple: la funció genera tots els nombres primers, només els nombres primers, i només el valor 2 apareix més d'una vegada. Tanmateix, ambdues fórmules es basen en el càlcul d'un factorial, el que les fa computacionalment inviables.
En la recerca d'aquestes funcions, s'han investigat notablement les funcions polinòmiques. Es pot afirmar que cap polinomi, fins i tot de diverses variables, no pren només valors primers per a valors enters de les variables. Per exemple, el polinomi d'una variable f(n) = n² -n +41 dona valors primers per a n =0..., 40, 43, però f(41) i f(42) són compostos. Tanmateix, hi ha polinomis de diverses variables els valors positius de les quals (quan les variables recorren els nombres naturals) són precisament els nombres primers. Un exemple és aquest polinomi descobert per Jones, Sato, Wada i Wiens el 1976:
Igual que amb les fórmules amb factorials, emprar aquest polinomi no és pràctic, ja que, encara que els valors positius que pren són tots primers, pràcticament no dona cap altra cosa que valors negatius quan es fan variar les variables a a z de 0 a infinit.
Un altre enfocament al problema de trobar una funció que només generi nombres primers ve donat a partir del teorema de Mills, que indica que existeix una constant tal que
és sempre un nombre primer, on és la funció part entera. No es coneix cap fórmula per calcular la constant de Mills, i les aproximacions que s'empren en l'actualitat es basen en la successió dels anomenats nombres primers de Mills (els nombres primers generats mitjançant aquesta fórmula), que no es poden obtenir rigorosament, sinó només de manera probabilística, suposant certa la hipòtesi de Riemann.
Algorismes de factorització[modifica]
Un algorisme de factorització és el que resol el problema d'expressar un nombre com a producte dels seus factors primers. Si es té un algorisme per trobar un factor d'un nombre, llavors el mateix algorisme serveix per expressar-lo com a producte dels seus factors primers. Només cal aplicar el mateix algorisme repetidament fins que tots els factors siguin nombres primers.
Després de la factorització per prova de divisions, els mètodes més antics que es coneixen són el métode de Fermat, que es basa en les diferències entre quadrats i que és especialment eficaç quan n és el producte de dos nombres primers propers entre si, i el mètode d'Euler, que es basa en la representació de n com a suma de dos quadrats de dues formes diferents.
Més recentment, s'han elaborat algorismes basats en una gran varietat de tècniques, com les fracciones contínues o les corbes el·líptiques, alguns són millores de mètodes anteriors com el garbell quadràtic, per exemple, que es basa en una millora del mètode de Fermat. D'altres, com el mètode rho de Pollard, són probabilístics, i no garanteixen trobar els divisors d'un nombre compost.
Actualment l'algorisme determinista més ràpid d'ús general és el garbell sobre el cos de nombres generalitzat, la complexitat computacional del qual és exponencial sobre el nombre de xifres de n.[19] S'ha proposat un algorisme de temps d'execució polinòmic sobre el nombre de xifres de n (l'Algorisme de Shor), però cal executar-lo en un ordinador quàntic, ja que la seva simulació en un ordinador normal requereix un temps exponencial.
Distribució[modifica]

Donat el fet que hi ha una infinitat de primers, és natural cercar patrons o irregularitats en la distribució dels nombres primers. El problema de modelar la distribució dels nombres primers és un tema de recerca popular per teòrics de nombres. L'aparició de nombres primers individuals entre els nombres naturals és (per ara) imprevisible, tot i que hi ha lleis (com el teorema dels nombres primers i el postulat de Bertrand) que governen la seva distribució mitjana. Leonhard Euler va dir:
| « | Els matemàtics han intentat en va, fins a la data, de descobrir algun ordre en la successió dels nombres primers, i tenim raons per creure que és un misteri al qual mai no penetrarà la ment.[20] | » |
En una classe el 1975, Don Zagier va comentar:
| « | Hi ha dos fets sobre la distribució de nombres primers dels quals espero convèncer-vos de manera tan aclaparadora que restaran gravats permanentment als vostres cors. El primer és que, malgrat la seva definició simple i el seu paper com els blocs constructius dels nombres naturals, els nombres primers creixen com les males herbes entre els nombres naturals, sembla que no obeeixin cap altre llei del que la de la casualitat, i ningú pot pronosticar on brotarà el pròxim. El segon fet és fins i tot més sorprenent, perquè diu precisament el contrari: que els nombres primers exhibeixen una regularitat atordidora, que hi ha lleis que governen el seu comportament, i que obeeixen aquestes lleis amb precisió gairebé militar.[21] | » |
Euler va observar que la funció
- n² + n + 41
Dona nombres primers per n ≤ 40 (però no necessàriament per n més gran), un fet notable que porta a aprofundir en la teoria algebraica de nombres, de forma més específica en els nombres de Heegner. L'espiral de Ulam representa tots els nombres naturals en una gràfica de tipus espiral. De forma sorprenent els nombres primers s'agrupen en certes diagonals i no en altres.
La quantitat de nombres primers més petits que un nombre donat[modifica]

La funció de recompte de nombres primers π(n) es defineix com la quantitat de nombres primers més petits o iguals que n. Per exemple π(11) = 5, ja que hi ha cinc primers més petits o iguals que 11. Es coneixen algorismes per calcular valors exactes de π(n) més ràpidament que contant cada primer fins a n. Valors tan grans com π(1020) es poden calcular ràpida i acuradament amb els ordinadors moderns.
Per valors més grans de n, més enllà de l'abast dels equips moderns, el teorema dels nombres primers proporciona una estimació: π(n) és aproximadament n/ln(n). En altres paraules, a mesura que n es fa molt gran, la probabilitat que un nombre més petit que n sigui primer és inversament proporcional al nombre de dígits en n. Es coneixen estimacions fins i tot millors; vegeu per exemple teorema dels nombres primers#La funció de recompte de nombres primers en termes de la integral logarítmica.
Si n és un enter positiu més gran que 1, llavors hi ha sempre un nombre primer p amb n < p < 2n (El postulat de Bertrand).
Distància entre nombres primers[modifica]
Una successió d'enters consecutius, cap dels quals no és primer, constitueix un buit entre nombres primers. Hi ha buits entre primers arbitràriament llargs: per a qualsevol nombre natural n més gran que 1, la successió (la notació n! s'ha de llefir factorial de n)
- n! + 2, n! + 3, …, n! + n
és una successió de n − 1 naturals compostos consecutius, ja que
- n! + m = m · (1 · 2 · … · (m − 1) · (m + 1) … n + 1)
és compost per qualsevol 2 ≤ m ≤ n. D'altra banda, els forats es fan arbitràriament petits en proporció a la quantitat de nombres primers: el quocient
- (pi + 1 − pi) / pi,
on pi denota el ièsim nombre primer (és a dir, p1 = 2, p₂ = 3, etc.), tendeix cap a zero quan i tendeix a infinit.
Aplicacions[modifica]
Durant molt de temps, la teoria de nombres en general, i l'estudi dels nombres primers en particular, era vist com l'exemple canònic de matemàtiques pures, sense aplicacions a fora del mateix interès d'estudiar el tema. En particular, teòrics de nombres com ara el matemàtic britànic G. H. Hardy se setien orgullosos de fer una feina que no tenia absolutament gens d'importància militar.[22] Tanmateix, aquesta visió quedava esmicolada als anys 1970, quan s'anunciava públicament que els nombres primers es podrien fer servir com la base per la creació d'algorismes de criptografia de clau pública. Els nombres primers també s'utilitzen per construir les taules hash i els generadors de nombres pseudoaleatoris.
Quan es dissenyen engranatges els nombres de dents de les rodes dentades es procura triar-los de forma que siguin nombres primers o parelles de nombres primers entre ells. D'aquesta manera cada dent d'una de les rodes entra en contacte el mateix nombre de vegades amb cada una de les dents de l'altra roda i el desgast és uniforme.
Aritmètica mòdul un nombre primer p[modifica]
L'aritmètica modular és una modificació de l'aritmètica usual, basada a fer tots els càlculs "mòdul" un nombre fixat n. Tots els càlculs en aritmètica modular tenen lloc en el conjunt finit
- {0, 1, 2, ..., n − 1}.
Calcular mòdul n vol dir que les sumes, les restes i les multiplicacions es fan normalment, però en acabar es pren com a resultat el residu de dividir entre n. Per exemple, sigui n = 7. Llavors, en aritmètica mòdul 7, la suma 3 + 5 és 1 en comptes de 8, perquè 8 dividit entre 7 dona de residu 1. De manera similar, 6 + 1 = 0 mòdul 7, 2 − 5 = 4 mòdul 7 (ja que −3 + 7 = 4) i 3 • 4 = 5 mòdul 7 (12 té per residu 5). Les propietats habituals de la suma i la multiplicació que compleixen els sistemes de nombres com els enters o els racionals es continuen complint, per exemple
- (a + b) · c = a · c + b · c (propietat distributiva).
Però, en general, no és possible dividir en aquest sistema. Per exemple, per n = 6, l'equació
- 3 · x = 2 (mòdul 6),
No es pot resoldre per obtenir-ne una solució x que seria l'anàleg a 2/3. Això es pot veure calculant 3 • 0, ..., 3 • 5 mòdul 6 (no hi ha cap resultat que sigui 2). La característica distintiva dels nombres primers és la següent: la divisió és possible en aritmètica modular si i només si n és un nombre primer. Per n = 7, l'equació
- 3 · x = 2 (mòdul 7)
Té una solució única, x = 3. De forma equivalent, n és un nombre primer si i només si tots els enters m que satisfan 2 ≤ m ≤ n − 1 són coprimers amb n, és a dir, el seu màxim comú divisor és 1. Fent servir la funció totient d'Euler φ, n és un nombre primer si i només si φ(n) = n − 1.
El conjunt {0, 1, 2, ..., n − 1}, amb aquesta suma i aquesta multiplicació es denota Z/nZ per a tot n. En termes d'àlgebra abstracta, és un anell, per a qualsevol n, però és un cos finit si i només si n és un nombre primer. Hi ha certs teorems que es poden obtenir analitzant Z/pZ de forma abstracta. Per exemple el petit teorema de Fermat, que estableix que ap − a és divisible entre p per a qualsevol nombre a, es pot demostrar fent servir aquests conceptes. Una conseqüència d'això és el que segueix: si p és un nombre primer diferent de 2 i 5, ¹/p és empre un nombre decimal periòdic, el període del qual és p − 1 o un divisor de p − 1.¹/p igualment si s'expressa en base q (en comptes de base 10) s'obté el mateix efecte, en cas que p no sigui un factor primer de q. El teorema de Wilson diu que un enter p > 1 és primer si i només si el factorial (p − 1)! + 1 és divisible entre p. Recíprocament, un enter n > 4 és compost si i només si (n − 1)! és divisible entre n.
Criptografia de clau pública[modifica]
L'algorisme RSA es basa en l'obtenció de la clau pública mitjançant la multiplicació de dos nombres grans (majors que 10100) que siguin primers. La seguretat d'aquest algorisme radica en el fet que no hi ha maneres ràpides de factoritzar un nombre gran en els seus factors primers utilitzant ordinadors tradicionals. La computació quàntica podria proveir una solució a aquest problema de factorització.
Nombres primers a la natura[modifica]

Inevitablement, alguns dels nombres que es donen a la natura són primers. Hi ha, tanmateix, relativament pocs exemples de nombres que apareixen en la natura perquè són primers. Per exemple, la majoria de les estrelles de mar tenen 5 braços, i 5 és un nombre primer. Tanmateix no hi ha cap prova que suggereixi que les estrelles de mar tenen 5 braços perquè 5 és un nombre primer. De fet, algunes estrelles de mar tenen un nombre de braços diferent. La Echinaster luzonicus normalment en té sis, la Luidia senegalensis en té nou, i la Solaster endeca en pot tenir fins a vint, de braços. El perquè la majoria d'estrelles de mar (i altres equinoderms) tenen simetria pentagonal continua sent un misteri.
Un exemple de l'ús de nombres primers en la natura és una estratègia evolutiva que fan servir les Cicadidae del gènere Magicicada.[23] Aquests insectes passen la majoria de les seves vides com a larves sota terra. Només es transformen en pupes i llavors emergeixen dels seus amagatalls després de 13 o 17 anys, en aquest punt volen, crien, i llavors moren en unes quantes setmanes com a màxim. Es creu que la raó de què els intervals entre emergències sigui un nombre primer és perquè això fa molt difícil que els predadors en evolucionar es puguin especialitzar com predadors de Magicicadas.[24] Si les Magicicadas apareguessin a intervals que no fossin nombres primers, per exemple cada 12 anys, llavors els predadors que apareguessin cada 2, 3, 4, 6, o 12 anys podrien assegurar-se de trobar-les. Durant un període de 200 anys, les poblacions mitjanes de predadors durant brots hipotètics de 14 i 15 anys serien fins a un 2% més altes que per a brots de 13 o 17 anys.[25] Encara que petit, aquest avantatge sembla haver estat prou per conduir la selecció biològica a favor d'un cicle de vida de basat en un nombre primer per a aquests insectes.
S'especula de què els zeros de la funció zeta de Riemann estan connectats als nivells d'energia de sistemes quàntics complexos.[26]
Generalitzacions[modifica]
El concepte de nombre primer s'ha generalitzat de diferents maneres en diferents branques de les matemàtiques. En general "primer" indica que és mínim o que no es pot descompondre en components més petits. Per exemple un cos primer és el subcos més petit d'un cos F que conté 0 i 1. Sovint es busca un segon significat addicional a aquest en fer servir la paraula primer, en el sentit que un objecte es pot descompondre de forma única en els seus components primers.
Elements primers en anells[modifica]

El concepte de nombres primers dona lloc a dos conceptes més generals que s'apliquen a elements de qualsevol anell A, (una estructura algebraica on s'han definit l'addició, la subtracció i la multiplicació): elements primers i elements irreductibles. Una element p de A s'anomena primer si no és una unitat (és a di si no és el seu propi element invers per la multiplicació) i es compleix la següent propietat: donats x i y a A tals que p és un divisor del producte, llavors p és divisor com a mínim un factor (x o y). Els elements irreductibles són els que no es poden escriure com a producte de dos elements de l'anell que no siguin unitats. En general, aquesta és una condició més feble, però per a qualsevol anell factorial, com l'anell Z dels enters, el conjunt d'elements primers és igual al conjunt d'elements irreductibles, que per a Z és {…, −11, −7, −5, −3, −2, 2, 3, 5, 7, 11, …}.
Un exemple habitual són els nombres enters de Gauss Z[i], és a dir, el conjunt de nombres complexos de la forma a + bi amb a i b a Z. Això és un anell íntegre, els seus elements primers es coneixen com a nombres primers de Gauss. No tots els primers en Z són primers de Gauss: a l'anell més gran Z[i], el nombre 2 es descompon en el producte dels dos primers de Gauss (1 + i) i (1 − i). Els nombres primers racionals (és a dir els elements primers de Z) de la forma 4k + 3 són primers de Gauss, mentre que els primers racionals de la forma 4k + 1 no ho són. Els primers de Gauss es poden fer servir per demostrar la llei de reciprocitat quadràtica, mentre que els primers d'Eisenstein tenen un paper similar en la llei de reciprocitat cúbica.
Ideals primers[modifica]
En teoria d'anells, el concepte de nombre se substitueix pel d'ideal. Els ideals primers són els que si el producte de dos elements xy pertany a l'ideal, llavors o bé x pertany a l'ideal o bé y pertany a l'ideal (o bé tots dos), això generalitza els elements primers en el sentit que l'ideal principal generat per un element primer és un ideal primer, són una eina important i són objecte d'estudi en àlgebra commutativa, teoria algebraica de nombres i geometria algebraica. Els ideals primers de l'anell dels enters són els ideals (0), (2), (3), (5), (7), (11), … El teorema fonamental de l'aritmètica es generalitza al teorema de Lasker-Noether que expressa qualsevol ideal en un anell commutatiu de Noether com la intersecció d'ideals primers, que és la generalització adequada de les potències dels nombres primers.[27]
Els ideals primers són els punts dels objectes àlgebro-geomètrics, a través del concepte d'espectre d'un anell. La geometria aritmètica també se'n beneficia d'aquest concepte, i hi ha molts paral·lelismes entre la teoria de nombres i la geometria. Per exemple, la descomposició en factors o ramificació d'ideals primers quan se sotmeten a una extensió d'un cos, és un problema bàsic en teoria algebraica de nombres que comporta certa similitud amb la ramificació en geometria. En l'exemple dels enters de Gauss, el (2) es ramifica en potència d'un primer (ja que 1 + i y 1 − i generen el mateix ideal primer), els ideals primers de la forma 4k + 3 són inerts (mantenen la seva primalitat) i els de la forma 4k + 1 passen a ser producte de dos ideals primers diferents.
Teoria de grups[modifica]
En teoria de grups, els grups esporàdics es consideren l'equivalent dels nombres primers. Es demostra que un grup simple finit pot ser: cíclic, alternat, un dels 16 tipus de grups simples finits de Lie o un dels 26 grups esporàdics.
Primers en teoria de l'avaluació[modifica]
En teoria algebraica de nombres apareix una altra generalització. Donat un cos , es prenen les avaluacions sobre , determinades funciones de en . Cada una d'aquestes avaluacions genera una topologia sobre . Es diu que dues avaluacions son equivalents si generen la mateixa topologia. Un primer de és una classe d'equivalència d'avaluacions. Amb aquesta definició, els primers del cos dels nombres racionals queden representats per la funció valor absolut així com per les avaluacions p-àdiques sobre per cada nombre primer p.
Nusos primers[modifica]
 |
 |

| |
| Alguns nusos primers | |||
En teoria de nusos, un nus primer és un nus no trivial que no es pot descompondre en dos nusos més petits. De forma més precisa, es tracta d'un nus que no es pot escriure com suma connexa de dos nusos no trivials.
L'any 1949 Horst Schubert va demostrar un teorema de factorització anàleg al teorema fonamental de l'aritmètica, que assegura que cada nus es pot obtenir de forma única com a suma connexa de nusos primers.[28] Per aquest motiu, els nusos primers tenen un paper fonamental a la teoria de nusos: una classificació dels nusos ha estat el tema central de la teoria des del segle xix.
Nombres primers en l'art i la literatura[modifica]
Els nombres primers han influït en nombrosos artistes i escriptors. El compositor francès Olivier Messiaen es va valer d'ells per crear música no mètrica. En obres tals com La Nativité du Seigneur (1935) o Quatre études de rythme empra simultàniament motius la durada dels quals és un nombre primer per crear ritmes impredictibles. Segons Messiaen, aquesta forma de compondre va ser «inspirada pels moviments de la naturalesa, moviments de durades lliures i desiguals».[29]
A la seva novel·la de ciència-ficció Contact, posteriorment adaptada al cinema, Carl Sagan suggereix que els nombres primers es podrien emprar per comunicar-se amb intel·ligències extraterrestres, una idea que havia desenvolupat de manera informal amb l'astrònom nord-americà Frank Drake el 1975.[30]
El curiós incident del gos a mitjanit, que descriu en primera persona la vida d'un jove autista molt dotat en matemàtiques i càlcul mental, fa servir només els nombres primers per numerar els capítols.
A la novel·la PopCo de Scarlett Thomas, l'àvia d'Alice Butler treballa en la demostració de la hipòtesi de Riemann. El llibre il·lustra una taula dels mil primers nombres primers.[31]
La solitudine dei numeri primi, novel·la escrita per Paolo Giordano, va guanyar el premi Strega el 2008.
També hi ha moltes pel·lícules que reflecteixen la fascinació popular cap als misteris dels nombres primers i la criptografia, per exemple, Cube, Sneakers, L'amor té dues cares i Una ment meravellosa. Aquesta última es basa en la biografia del matemàtic i premi Nobel John Forbes Nash, escrita per Sylvia Nasar.[32]
Referències[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Nombre primer |
- ↑ Corbalán Yuste, F. et al.. Gamma 2 : matemàtiques : Educació Secundària, segon curs. 1a.. Barcelona: Vicens Vives, 2003, p. 6. ISBN 84-316-6978-2.
- ↑ Niven- Zuckerman: Introducción a la teoría de números
- ↑ Marcus du Sautoy, La symphonie des nombres premiers P.42 (francès)
- ↑ Préhistoire de la géométrie: le problème des sources Arxivat 2007-07-10 a Wayback Machine., article de Olivier Keller (francès)
- ↑ Joseph Needham (Ed.) Mathematics and the Sciences of the Heavens and the Earth Science and Civilisation in China, Vol. 3 Ch. 19 Cambridge University Press, 1959
- ↑ The Largest Known Prime by Year: A Brief History Prime Curios!: 17014... 05727 (39 xifres) (anglès)
- ↑ Hans Riesel, 'Prime Numbers and Computer Methods for Factorization '. New York: Springer (1994): 36 (anglès)
- ↑ Richard K. Guy & John Horton Conway, 'The Book of Numbers '. New York: Springer (1996): 129 -130 (anglès)
- ↑ Gowers, T. Mathematics: A Very Short Introduction. Oxford University Press, 2002, p. 118. ISBN 0-19-285361-9. «L'exclusió aparentment arbitrària de l'1 de la definició de nombre primer ... no expressa cap coneixement profund sobre els nombres: es tracta simplement d'un conveni útil, adoptat perquè només hi hagi una manera de factoritzar qualsevol nombre»
- ↑ ""Why is the number one not prime? " ". Retrieved 2007-10-02.
- ↑ ""Arguments for and against the primality of 1 " (anglès)
- ↑ Siegmund-Schultze, Reinhard «Euclid's Proof of the Infinitude of Primes: Distorted, Clarified, Made Obsolete, and Confirmed in Modern Mathematics» (pdf) (en anglès). The Mathematical Intelligencer, vol. 36, núm. 4, 2014, pàg. 87-97 [Consulta: 6 març 2015].
- ↑ «The Largest Known prime by Year: A Brief History» (en anglès). Chris K. Caldwell, 31-12-2020. [Consulta: 18 gener 2021].
- ↑ A data maig de 2007.
- ↑ Vegeu la llista actualitzada de primers de Sophie Germain.
- ↑ The Prime Pages - el major parell conegut de primers bessons
- ↑ The Prime Pages
- ↑ Introducción del capítol 3 del llibre de Ribenboim The new book of prime number records.
- ↑ Error en el títol o la url.«».
- ↑ Havil 2003, p. 163
- ↑ Havil 2003, p. 171
- ↑ Hardy, G.H.. A Mathematician's Apology. Cambridge University Press, 1940. ISBN 0-521-42706-1. «No one has yet discovered any warlike purpose to be served by the theory of numbers or relativity, and it seems unlikely that anyone will do so for many years»
- ↑ Goles, E., Schulz, O. and M. Markus (2001). "Prime number selection of cycles in a predator-prey model", Complexity 6(4): 33-38
- ↑ Paulo R. A. Campos, Viviane M. de Oliveira, Ronaldo Giro, and Douglas S. Galvão. «Emergence of Prime Numbers as the Result of Evolutionary Strategy». Phys. Rev. Lett., 93, 2004, pàg. 098107. DOI: 10.1103/PhysRevLett.93.098107 [Consulta: 26 novembre 2006].
- ↑ «Invasion of the Brood». The Economist, 06-05-2004. [Consulta: 26 novembre 2006].
- ↑ Ivars Peterson. «The Return of Zeta». MAA Online, 28-06-1999. Arxivat de l'original el 1999-11-05. [Consulta: 14 març 2008].
- ↑ Eisenbud 1995, section 3.3.
- ↑ A Mathworld. (anglès)
- ↑ Peter Hill. Amadeus Press. The Messiaen companion, 1994. ISBN 0-931340-95-0.
- ↑ Carl Pomerance, Prime Numbers and the Search for Extraterrestrial Intelligence, Revisat el 22-12-2007
- ↑ «- A Mathematician reviews PopCo». Arxivat de l'original el 2008-12-12. [Consulta: 22 abril 2009].
- ↑ Music of the Spheres Arxivat 2015-10-09 a Wayback Machine., Selecció de Marcus du Sautoy de pel·lícules que versen sobre els nombres primers (anglès)
Vegeu també[modifica]
| A Viquillibres hi ha llibres de contingut lliure i altres textos relatius a Taula de factors primers. |





































