Corba el·líptica

En matemàtiques, una corba el·líptica és una corba plana definida per una equació de la forma
- y² = x3 + a x + b,
que no és singular; és a dir, la seva gràfica no té cúspides o punts d'intersecció amb ella mateixa. (Quan la característica del cos de coeficients és 2 o 3, l'equació anterior no és suficientment general per a incloure totes les corbes cúbiques no singulars; vegeu més endavant per a una definició més precisa).
Es pot veure que les corbes el·líptiques es corresponen a embeddings del tor al pla projectiu; aquests embeddings es poden generalitzar a cossos arbitraris. Així, es diu que les corbes el·líptiques són corbes algebraiques projectives de gènere 1 sobre un cos K, juntament amb un punt distingit definit sobre K. L'estructura de grup natural del tor es manifesta d'una forma geomètricament curiosa en les corbes el·líptiques; el conjunts de punts de la corba forma un grup abelià.
Les corbes el·líptiques són especialment importants en la teoria de nombres, i constitueixen una àrea de recerca actual molt important; per exemple, foren usades per Andrew Wiles en la demostració del darrer teorema de Fermat. També tenen múltiples aplicacions en la criptografia (vegeu criptografia sobre corbes el·líptiques) i en la factorització d'enters.
Corbes el·líptiques sobre els nombres reals[modifica]
Tot i que la definició formal d'una corba el·líptica és una mica tècnica i demana una mica de coneixements previs de geometria algebraica, és possible descriure alguns aspectes de les corbes el·líptiques sobre els nombres reals fent ús només de l'àlgebra i geometria de secundària.
En aquest context, una corba el·líptica és una corba plana definida per l'equació de la forma
- ,
on a i b són nombres reals. Aquest tipus d'equació s'anomena equació de Weierstrass.
Per exemple, el següent dibuix il·lustra les corbes el·líptiques donades per les equacions i .
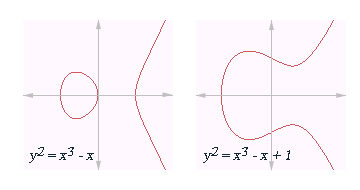
La definició de corba el·líptica exigeix també que la corba sigui no singular. Geomètricament, això significa que la gràfica no té cúspides ni punts d'intersecció amb ella mateixa. Algebraicament, això implica el càlcul del discriminant,
La corba és no singular si el discriminant no és igual a zero. (Encara que el factor −16 és irrellevant quan es considera sobre el cos dels nombres reals, esdevé necessari sobre altres cossos).
La gràfica d'una corba no singular, té dues components si el seu discriminant és positiu, i un de sol si és negatiu. Per exemple, en les representacions mostrades anteriorment, el primer discriminant és 64, i el segon és −368.
La llei de grup[modifica]
Adjuntant un "punt de l'infinit", obtenim una versió projectiva de la corba. Si P i Q són dos punts de la corba, aleshores podem trobar un únic tercer punt que és la intersecció de la corba amb la línia que passa per P i Q. Si la línia és tangent a la corba en un punt, aleshores aquest punt es compta dues vegades; i si la línia és paral·lela a l'eix de les y, definim el tercer punt com el "punt de l'infinit". Així sempre se satisfà exactament una d'aquestes condicions per a qualsevol parella de punts de la corba el·líptica.
Així, és possible d'introduir una operació de grup, "+", a la corba amb les següents propietats: considerem el punt de l'infinit com l'element neutre 0; i si una línia recta interseca amb la corba als punts P, Q i R, aleshores imposem que P + Q + R = 0 en el grup. Es pot comprovar que d'aquesta operació en resulta un grup abelià, i per tant una varietat abeliana. Es pot demostrar que el conjunt de punts K-racionals (incloent el punt de l'infinit) forma un subgrup d'aquest grup. Si denotem la corba per E, normalment escriurem doncs E(K) per denotar aquest subgrup.
El grup esmentat, es pot descriure tant algebraicament com geomètricament. Donada la corba y² = x3 − px − q sobre el cos K (la característica del qual suposem que no és ni 2 ni 3), i els punts P = (xP, yP) i Q = (xQ, yQ) de la corba, suposem primer que xP ≠ xQ. Sigui s = (yP − yQ)/(xP − xQ); com que K és un cos, s està ben definit. Aleshores podem definir R = P + Q = (xR, yR) mitjançant
Si xP = xQ, aleshores hi ha dues opcions: si yP = −yQ, aleshores la suma es defineix com a 0; així, l'invers de cada punt de la corba es troba reflectint el punt sobre l'eix de les x. Si yP = yQ ≠ 0, aleshores R = P + P = 2P = (xR, yR) ve donat per
Si yP = yQ = 0, aleshores P + P = 0.
Corbes el·líptiques sobre els nombres complexos[modifica]
La formulació de les corbes el·líptiques com a embedding d'un tor en el pla projectiu complex ve donada naturalment gràcies a una curiosa propietat de les funcions p de Weierstrass. Aquestes funcions i les seves primera derivades estan relacionades mitjançant la fórmula
Aquí, and són constants; és la funció P de Weierstrass i la seva derivada. És clar que aquesta relació és en forma de corba el·líptica (sobre els nombres complexos. Les funcions de Weierstrass són doblement periòdiques; això vol dir que són periòdiques respecte a una xarxa Λ; bàsicament, les funcions de Weierstrass estan definides naturalment sobre un tor . Es pot trobar un embedding del tor al pla projectiu mitjançant l'aplicació
- .
Aquesta aplicació és un isomorfisme de grups, el qual porta l'estructura de grup del tor al pla projectiu. És també un isomorfisme de superfícies de Riemann, així topològicament una corba el·líptica donada és com un tor. Si la xarxa Λ està relacionada amb la xarxa cΛ mitjançant la multiplicació pel nombre complex c diferent de zero, aleshores les corbes corresponents són isomorfes. Les classes d'isomorfismes de corbes el·líptiques venen donades per l'invariant j.
Les classes d'isomorfismes es poden entendre també d'una forma més senzilla. Les constants i , anomenades invariants modulars, estan determinades únicament per la xarxa, és a dir, per l'estructura del tor. Tanmateix, els nombres complexos són el cos de descomposició dels polinomis, i per tant podem veure la corba el·líptica com
Es veu que
i
i per tant el discriminant modular és
Aquí, λ se l'anomena de vegades la funció modular lambda.
Cal destacar que el teorema d'uniformització ens diu que es pot representar tota superfície de Riemann compacta de gènere 1 com un tor.
Corbes el·líptiques sobre un cos general[modifica]
Les corbes el·líptiques es poden definir sobre qualsevol cos K; la definició formal d'una corba el·líptica és una corba algebraica projectiva no singular sobre K de gènere 1 amb un punt donat definit sobre K.
Si la característica de K no és ni 2 ni 3, aleshores podem escriure tota corba el·líptica sobre K en la forma
- y² = x3 − px − q
on p i q són elements de K tals que el polinomi de la dreta x3 − px − q no té arrels dobles. Si la característica és 2 o 3, s'ha de tenir en consideració més termes.
Generalment es prenen les corbes com al conjunt de punts (x,y) que satisfan l'equació anterior i tals que tant x com y són elements de la clausura algebraica de K. S'anomenen punts K-racionals als punts tals que llurs coordenades pertanyen a K.
Connexions amb la teoria de nombres[modifica]
El teorema de Mordell-Weil diu que si K és el cos dels nombres racionals (o més generalment, un cos de nombres), aleshores el grup de punts K-racionals és finitament generat. Això vol dir que es pot expressar el grup com a suma directa d'un grup abelià lliure i un grup de torsió finit. Mentre que la torsió d'un subgrup d'E(K) és relativament fàcil de determinar, en general no es coneix cap algorisme per a calcular el rang del subgrup lliure. La conjectura de Birch i Swinnerton-Dyer dona una fórmula per a calcular aquest rang.
La recent demostració del darrer teorema de Fermat s'efectuà amb la demostració d'un cas especial de la conjectura de Taniyama-Shimura en el qual es relacionen les corbes el·líptiques sobre els racionals amb les formes modulars; aquesta conjectura fou demostrada completament el 1999.
Mentre que el nombre exacte de punts racionals d'una corba el·líptica E sobre un cos finit Fq és generalment difícil de calcular, el teorema de Hasse sobre corbes el·líptiques ens diu que
Podem entendre i demostrar aquest fet amb l'ajuda d'una teoria més general; consulteu funció zeta local o cohomologia étal.
El nombre exacte de punts d'una corba particular es pot calcular amb l'algorisme de Schoof.
Algorismes que usen corbes el·líptiques[modifica]
Les corbes el·líptiques sobre cossos finits s'usen en diverses aplicacions criptogràfiques així com per a la factorització d'enters. Típicament, la idea general per a aquestes aplicacions és que un algorisme ja conegut que s'aplica sobre certs grups finits, es reescriu per tal de ser usat en el grup de punts racionals d'una corba el·líptica.
Bibliografia[modifica]
Serge Lang, a la introducció del llibre que se cita a continuació, diu que "és possible escriure sense fi sobre corbes el·líptiques. (No és cap amenaça)". La següent és una llista ben curta d'alguns llibres (en anglès) que poden servir com a guia davant la immensa quantitat de bibliografia que hi ha disponible sobre els aspectes teòrics, algorítmics i criptogràfics de les corbes el·líptiques.
- I. Blake; G. Seroussi, N. Smart, N.J. Hitchin. Elliptic Curves in Cryptography. Cambridge Univ. Press, 2000. ISBN 0-521-65374-6.
- Richard Crandall; Carl Pomerance. «Chapter 7: Elliptic Curve Arithmetic». A: Prime Numbers: A Computational Perspective. Springer, 2001, p. 285–352. ISBN 0-387-94777-9.
- John Cremona. Algorithms for Modular Elliptic Curves. Cambridge Univ. Press, 1992.
- Dale Husemöller. Elliptic Curves. 2a edició. Springer, 2004.
- Kenneth Ireland; Michael Rosen. «Chapters 18 and 19». A: A Classical Introduction to Modern Number Theory. 2a edició. Springer, 1990.
- Anthony Knapp. Elliptic Curves. Math Notes 40, Princeton Univ. Press, 1992.
- Neal Koblitz. Introduction to Elliptic Curves and Modular Forms. Springer, 1984.
- Neal Koblitz. «Chapter 6». A: A Course in Number Theory and Cryptography. 2a edició. Springer, 1994. ISBN 0-387-94293-9.
- Serge Lang. Elliptic Curves: Diophantine Analysis. Springer, 1978.
- Joseph H. Silverman. The Arithmetic of Elliptic Curves. Springer, 1986.
- Joseph H. Silverman. Advanced Topics in the Arithmetic of Elliptic Curves. Springer, 1994.
- Joseph H. Silverman; John Tate. Rational Points on Elliptic Curves. Springer, 1992.
- Lawrence Washington. Elliptic Curves: Number Theory and Cryptography. Chapman & Hall/CRC, 2008. ISBN 1-58488-365-0.
Enllaços externs[modifica]
- LMFDB: Base de dades de corbes el·líptiques sobre Q (anglès)
- The Mathematical Atlas: 14H52 Corbes el·líptiques Arxivat 2003-02-23 a Wayback Machine. (anglès)






















