Nombre π

De Viquipèdia

Dreceres ràpides: navegació, cerca
Sistema de nombres en matemàtiques
Conjunts de nombres
ℕ ⊆ ℤ ⊆ ℚ ⊆ ℝ ⊆ ℂ
Nombres destacables
  • π ≈ 3,14159265...
  • e ≈ 2,7182818284...
  • Φ ≈ 1,6180339887...
  • i (amb i ² = −1)
Nombres amb propietats destacables

Primers, abundants, amics, compostos, defectius, perfectes, sociables, algebraics, transcendents
Extensions dels
nombres complexos
Nombres Especials
Altres nombres importants

Seqüència d'enters
Constants matemàtiques
Llistat de nombres
Nombres grans
Sistemes de numeració

Àrab, armeni, àtica (grega), babilònica, ciríl·lica, egípcia, etrusca, grega, hebrea, índia, jònica (grega), japonesa, khmer, maia, romana, tailandesa, xinesa.

En matemàtiques, π és la constant d'Arquimedes, una constant que relaciona el diàmetre de la circumferència amb la longitud del seu perímetre.

P = d · π

El símbol π es pronuncia [pi] i és la setzena lletra de l'alfabet grec.

π és un nombre irracional, és a dir, la seva part fraccionària té un nombre de xifres infinit, i no es pot establir un patró que determini quina serà la següent a una determinada. Per calcular s'acostuma a agafar el seu valor simplificat: 3,14159265.

El nombre π a més d'aparèixer en la fórmula de la longitud de la circumferència, apareix a totes les equacions matemàtiques derivades d'aquesta: superfície del cercle, superfície i volum de l'esfera... i també a nombroses equacions de la física.

Una circumferència de diàmetre 1 té de perímetre π.

Taula de continguts

[edita] Història

Article principal: història del nombre π

La història de π transcorre paral·lela al desenvolupament de les matemàtiques com un tot.[1] Alguns autors divideixen el seu desenvolupament en tres períodes: El període antic, durant el qual π es va estudiar des de un punt de vista geomètric, la era clàssica que neix amb el desenvolupament del càlcul infinitesimal a Europa al voltant del segle XVII i l'era dels ordinadors digitals.[2]

[edita] Període antic

Arquimedes. Quadre de Domenico Fetti 1620.

El fet de què la proporció entre el perímetre i el diàmetre és una constant per a totes les circumferències, i que és lleugerament més gran que 3, ja ho coneixien els geòmetres antics d'Egipte, Babilònia, India i Grècia. Les aproximacions més antigues conegudes són aproximadament del 1900 AC; són: 25/8 (Babilònia) i 256/81 (Egipte), les dues amb un error de menys de l'1% del valor real.[3] El text Indi Shatapatha Brahmana assigna a π el valor 339/108 ≈ 3.139. La Bíblia sembla que suggereixi, en el llibre dels reis, que π = 3, el que és clarament pitjor que altres estimacions disponibles a l'època d'escriure'l (600 AC). La interpretació d'aquest passatge és controvertida,[4][5]

Arquímedes (287-212 AC) va ser el primer que va estimar π de forma rigorosa. Se'n va adonar que la seva magnitud es pot fitar per davall i per damunt a base de inscriure i circumscriure circumferències a polígons regulars i calculat els perímetres d'aquests polígons:[5]

Archimedes pi.svg

Fent servir l'equivalent a polígons de 96 cares, va demostrar que 223/71 < π < 22/7.[5] Agafant la mitjana d'aquests valors s'obté 3.1419.

Fórmules d'Arquimedes
Propietat de la bisectriu

Arquimedes fa servir una propietat que relaciona el peu d'una bisectriu als costats adjacents: A la figura adjunta SS' és la bisectriu de l'angle de vèrtex S

\frac xa = \frac yb = \frac {x+y}{a+b}


Polígon circumscrit

Per al polígon circumscrit. A la figura, c1 i c2 són els semi-costats de dos polígons circumscrits consecutius. Arquimedes demostra, fent servir la propietat precedent, que

\frac{c_1}{c_2} = 1 + \frac{d_1}{r}
\frac{d_1}{r} = \sqrt{1+\left(\dfrac{c_1}{r}\right)^2}

i reitera 4 vegades l'operació a partir de l'hexàgon.


Polígon inscrit

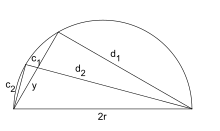
Per al polígon inscrit. A la figura adjunta, c1 i c2 són els costats de dos polígons inscrits consecutius. Arquimedes demostra, fent servir els triangles semblants i la propietat de la bisectriu que

\frac{d_2}{c_2} = \frac{2r}{y}=\dfrac{2r}{c_1}+ \frac{d_1}{c_1}
\frac{2r}{c_2} = \sqrt{1+\left(\dfrac{d_2}{c_2}\right)^2}

Actualment, les fórmules trigonomètriques permeten simplificar l'algorisme d'Arquimedes. Els perímetres pi i Pi dels polígons inscrits i circumscrits verifiquen les relacions de recurrència següents

\frac{1}{P_{n+1}} = \frac12 \left(\frac{1}{p_n} + \frac{1}{P_n}\right)
p_{n+1} = \sqrt{p_nP_{n+1}}

En efecte, per a una circumferència de raidi 1, si es nota 'an la meitat de l'angle en el centre dels polígons en l'etapa n, se sap que

p_n=2n\sin(a_n)\,
P_n=2n\tan(a_n)\,
p_{n+1} = 4n\sin(a_n/2)\,
P_{n+1} = 4n\tan(a_n/2)\,

i

\frac12 \left(\frac{1}{p_n} + \frac{1}{P_n}\right) = \frac{1}{4n}\frac{1+\cos(a_n)}{\sin(a_n)} = \frac{1}{4n}\frac{2\cos^2(a_n)}{2\sin(a_n/2)\cos(a_n/2)} = \frac{1}{4n}\frac{1}{\tan(a_n/2)}= \frac{1}{P_{n+1}}
\sqrt{p_nP_{n+1}}= \sqrt{8n^2\sin(a_n)\frac{\sin(a_n/2)}{cos(a_n/2}}=\sqrt{16n^2\sin^2(a_n/2)} = 4n\sin(a_n/2) = p_{n+1}
 

Mes tard al segle II AC, Ptolemeu, fent servir un 360-gon regular, va obtenir un valor de 3.141666...., que és correcte fins a la tercera xifra decimal.[6]

L'any 1116 el matemàtic català Savasorda fa servir l'aproximació 377/120 al seu Llibre de geometria. Aquesta és la mateixa aproximació que havia obtingut Tolemeu.[7]

Maimònides 1135, 1204 diu que π només es pot conèixer de forma aproximada i per tant que el valor de 3 que li assigna la bíblia era prou exacte per motius religiosos. Alguns han interpretat això com la primera afirmació de què π és irracional. [8]

Ramon Llull el 1299 al seu llibre De quadratura e triangulatura de cercle afirma que amb el compàs no es pot mesurar la circumferència, diu:[9]

« Com siasso que mesures de linyes dretes e mesures de linyes circulars no sien de una mateixa raho e ab lo compas hom no pusca mesurar linyes circulars ab linyes dretes, per aço coue en l'anjma mesurar linyes dretes e circulars ab la ymaginacio matematicalmen rehebent los significats de linyes dretes e circulars sentides en sobiet vesible  »

—Ramón Llull

Aquesta conjectura és equivalent a afirmar que π és irracional i a demés no és un nombre construïble.

[edita] Era clàssica

Leibnitz retrat de von B. Chr. Francke 1700.

El següent avenç essencial en l'estudi de π arribava amb el desenvolupament del càlcul infinitesimal, i en particular el descobriment de les sèries infinites que, en principi, permeten calcular π amb qualsevol precisió desitjada si s'afegeix una quantitat prou gran de termes. Al voltant del 1400 Madhava de Sangamagrama va trobar la primera d'aquestes sèrie s:

\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots\!

Avui es coneix com la sèrie de Madhava-Leibniz[10][11] o la sèrie de Gregory-Leibniz donat que va ser redescoberta per James Gregory i Gottfried Leibniz al segle XVII. Desgraciadament la velocitat de convergència és massa lenta per poder calcular gaires xifres a la pràctica; cal sumar al voltant de 4.000 termes per millorar l'estimació d'Arquimedes. Però, transformant la sèrie en

\pi = \sqrt{12} \, \left(1-\frac{1}{3 \cdot 3} + \frac{1}{5 \cdot 3^2} - \frac{1}{7 \cdot 3^3} + \cdots\right)\!

Madhava fou capç de calcular π com 3.14159265359, correcte en 11 xifres decimals. Aquest record el va batre el matematic persa Jamshīd al-Kāshī el 1424 que va determinar 16 decimals de π.

La primera contribució important europea des de Arquimedes la va fer el matemàtic alemany Ludolph van Ceulen (1540–1610), que va fer servir un mètode geomètric per calcular 35 decimals de π. Estava tan orgullós d'aquest càlcul, el qual li va portar la major part de la seva vida, que es va fer gravar les xifres a la seva tomba.[12]

Al voltant de la mateixa època, a Europa va començar a sorgir els mètodes del càlcul infinitessimal, la determinació de sèries infinites i els productes de quantitats geomètriques. La primera representació d'aquesta mena va ser la fórmula de Viète,

\frac2\pi = \frac{\sqrt2}2 \cdot \frac{\sqrt{2+\sqrt2}}2 \cdot \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2 \cdot \cdots\!
Leonhard Euler, 1707–1783, Retrat fet per Emanuel Handmann, 1753

que va trobar François Viète el 1593. Un altre resultat famós és el producte de Wallis,

\frac{\pi}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots\!

descobert per John Wallis rl 1655. El mateix Isaac Newton va trobar una sèrie per calcular π i va calcular 15 xifres, tot i que més tard va confessar: "Estic avergonyit d'explicar-vos la quantitat de nombres que vaig haver de fer per aquests càlculs, sense tenir altre cosa que fer en aquell temps." [13]

Es diu que William Jones al llibre A New Introduction to Mathematics de 1706 va ser el primer en fer servir la lletra grega π per representar aquesta constant, però aquesta notació es va popularitzar quan la va adotar Leonhard Euler el 1737.[14] Va escriure:

« Hi ha altres formes diverses de trobar les longituds o les àrees de línies corbes particulars, o plans, que podrien facilitar molt la pràctica; com per exemple, en la circumferència, el diàmetre és a al perímetre com 1 a (16/5 - 4/239) - 1/3(16/5^3 - 4/239^3) + ... = 3.14159... = π[3]  »

—Leonhard Euler

[edita] Era informàtica

Srinivasa Ramanujan.

A principis del segle XX, el matemàtic indi Srinivasa Ramanujan va trobar moltes fórmules per calcular π, algunes destaquen per la seva elegància i profunditat matemàtica.[15] Una de les seves fórmules és la sèrie,

\frac{1}{\pi} = \frac{2 \sqrt 2}{9801} \sum_{k=0}^\infty \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}\!

i la sèrie relacionada amb aquesta que van trobar els germans Chudnovsky el 1987,

\frac{426880 \sqrt{10005}}{\pi} = \sum_{k=0}^\infty \frac{(6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 (-640320)^{3k}}\!

que genera 14 xifres per cada terme.[15] Els Chudnovsky van fer servir aquesta fórmula per establir uns quants rècords de càlcul de π a finals dels 1980, incloent-hi el primer càlcul de més de un bilió de xifres decimals (1,011,196,691) el 1989. Continua sent la fórmula que es fa servir en els programari per calcular π en els ordinadors personals, contràriament als super ordinadors que es fan servir per establir els rècords moderns.

Mentre que les sèries normalment augmenten la precisió amb una quantitat fixa per cada terme afegit, hi ha algorismes iteratius que multipliquen el nombre de xifres correctes a cada pas. Un progrés significatiu es va fer el 1975, quan Richard Brent i Eugene Salamin independentment l'un de l'alre, van descobrir, l'algorisme de Brent-Salamin, que només fa servir aritmètica per doblar el nombre de xifres correctes a cada pas.[16] L'algorisme consisteix en establir

a_0 = 1 \quad \quad \quad b_0 = \frac{1}{\sqrt 2} \quad \quad \quad t_0 = \frac{1}{4} \quad \quad \quad p_0 = 1\!

i iterar

a_{n+1} = \frac{a_n+b_n}{2} \quad \quad \quad b_{n+1} = \sqrt{a_n b_n}\!
t_{n+1} = t_n - p_n (a_n-a_{n+1})^2 \quad \quad \quad p_{n+1} = 2 p_n\!

fins que an i bn estan prou aprop. Llavors l'estimació de π ve donada per

\pi \approx \frac{(a_n + b_n)^2}{4 t_n}.\!

Fent servir aquest sistema, amb 25 iteracions n'hi ha prou per obtenir 45 milions de decimals correctes. Jonathan i Peter Borwein van trobar un algorisme similar que quadruplica l'exactitud a cada pas.[17]

Un desenvolupament recent important va ser la fórmula de Bailey–Borwein–Plouffe (fórmula BBP), descoberta per Simon Plouffe i anomenada en honor als autors de l'article en què es va publicar la fórmula per primer cop, David H. Bailey, Peter Borwein, i Plouffe.[18]

La fórmula,

\pi = \sum_{k=0}^\infty \frac{1}{16^k} \left( \frac{4}{8k + 1} - \frac{2}{8k + 4} - \frac{1}{8k + 5} - \frac{1}{8k + 6}\right),

és singular perquè permet trobar qualsevol dígit individual hexadecimal o binari de π sense haver de calcular tots els precedents.[18] Entre el 1998 i el 2000, el projecte de computació distribuïda PiHex va fer servir una modificació de la fórmula BBP deguda a Fabrice Bellard per calcular el quatrilionèssim (1,000,000,000,000,000:èssim) bit de π, que va resultar ser 0.[19]

[edita] Definició

Perímetre = π × diàmetre

En geometria euclidiana π es defineix com la proporció entre el perímetre d'una circumferència i el seu diàmetre:[3]

\pi =\frac{Per\acute{i}metre}{Di\grave{a}metre}

El fet que aquesta proporció sigui constant, independentment de la mida de la circumferència, és el que permet que π es pugui definir. Per exemple si una circumferència té un diàmetre doble que un altre també té doble perímetre, per tant el quocient entre les dues magnituds és el mateix. Això es conseqüència de les propietats de les figures semblants. Euclides estableix que en les figures semblants totes les distàncies entre punts homòlegs guarden la mateixa proporció.[20]

Definició de πr2 en base a l'àrea del quadrat del radi.

Una forma alternativa de definir π és emprant la proporció entre l'àrea del cercle (A) i l'àrea del quadrat que té els costats de la mateixa longitud que el radi:[3][21]

\pi = \frac{A}{r^2}.

Aquesta definició es basa en què les àrees dels cercles són proporcionals als quadrats dels radis. Per exemple en duplicar el radi es multiplica per 4 l'àrea del seu quadrat, però també es multiplica per 4 l'àrea del cercle, de forma que el quocient es manté constant.[22]

Aquestes definicions depenen de la geometria, de fet en les demostracions es fa servir el cinquè postulat d'Euclides. En geometria no euclidiana les proporcionalitats no es mantenen i el quocient entre el perímetre de la circumferència i el seu diàmetre varia en variar el diàmetre.

Per aquest motiu els matemàtics sovint prefereixen definir π sense fer referència a qüestions geomètriques, en comptes d'això es tria una de les seves propietats analítiques per definir-lo. Una elecció habitual per definir π és: el dble del valor positiu de x per al qual la funció trigonomètrica cos(x) = 0.[23] En aquest article es donen moltes altres fórmules per calcular π que també es poden fer servir com a definició.

[edita] Fórmules relacionades amb π

[edita] Geometria

El·lipse amb semieixos a i b.
Relacionades amb la circumferència i amb el cercle.
Relacionades amb l'el·lipse
  • Àrea de l'el·lipse amb semieixos a i b: A = π ab
Relacionades amb l'esfera.
  • Volum de l'esfera de radi r: V = (4/3) π r3
  • Àrea de superfície d'una esfera de radi r: A = 4 π r2
Relacionades amb el cilindre.
  • El volum del cilindre d'altura h i radi de la base r és V = π r 2 h
  • L'àrea de la superfície del cilindre d'altura h i radi de la base r és A = 2 π r 2 + 2 π r h
Relacionades amb el conus.
  • Volum del conus de radi de la base r i altura h. V = (1/3) πr 2 h
  • Àrea de la superfície del conus de radi de la base r i altura h. A = π r (r + √ (h 2 + r 2) )

[edita] Anàlisi

\frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \frac{\pi}{4} (Fórmula de Leibniz)
\frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2} (producte de Wallis)
\zeta(2) = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6} (Euler)
\zeta(4)= \frac{1}{1^4} + \frac{1}{2^4} + \frac{1}{3^4} + \frac{1}{4^4} + \cdots = \frac{\pi^4}{90}
\int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi} (integral de Gauss)
\Gamma\left({1 \over 2}\right)=\sqrt{\pi}
n! \approx \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n (Fórmula de Stirling)
e^{\pi i} + 1 = 0\; (Identitat d'Euler, també anomenada "La fórmula més important del món")

Hi ha diverses representacions de &pi en fraccions contínues:[24]

\frac{4}{\pi} = 1 + \frac{1}{3 + \frac{4}{5 + \frac{9}{7 + \frac{16}{9 + \frac{25}{11 + \frac{36}{13 + ...}}}}}}
Càlcul de &pi pel mètode de Montecarlo.

[edita] Teoria de nombres

La probabilitat que dos nombres triats aleatòriament siguin coprimers és de 6/π2.
La probabilitat que un enter triat aleatòriament no tingui cap factor primer elevat a una potència superior a 1 (sigui lliure de quadrats) és de 6/π2.
Una manera empírica de trobar el valor de pi: dibuixeu un quadrat de costat 'l' a la paret. Tireu un dard dins el quadrat tantes vegades com pugueu sense apuntar enlloc més que a dins del quadrat. Dibuixeu un cercle de diàmetre 'l' inscrit en el quadrat. Compteu 'nc' el nombre de vegades que el dard ha anat dins la circumferència, i 'nq' nombre de vegades que el dard ha anat dins del quadrat però fora de la circumferència. Per probabilitat i relacionant l'àrea dels dos polígons es pot deduir que π ≅ 4*nc/(nc+nq), i que és més exacte (o sigui, més decimals) com més vegades haguem tirat el dard. Aquesta prova també es pot fer sobre paper quadriculat comptant les interseccions com a punts on ha anat el dard.
En altres paraules: π/4 és la probabilitat que la suma dels quadrats de dos nombres aleatoris iguals o majors que 0, i menors o iguals a la unitat, sia menor o igual que 1.

[edita] Aproximacions de pi

[edita] Aproximacions històriques

Article principal: Història del nombre π

Algunes aproximacions històriques de valors de π, es presenten a la següent taula:

Any Matemàtic o document Cultura Aproximació Error

(en parts per milió)
~1900 a. C. Papir de Rhind Egípcia 28/34 ~ 3,1605 6016 ppm
~1600 a. C. Tauleta de Susa Babilònica 25/8 = 3,125 5282 ppm
~600 a. C. La Bíblia (Reis I, 7,23) Jueva 3 45070 ppm
~500 a. C. Bandhayana India 3,09 16422 ppm
~250 a. C. Arquimedes de Siracusa Grega entre 3 10/71 y 3 1/7

usà 211875/67441 ~ 3,14163

 <402 ppm

13,45 ppm
~150 Claudi Ptolemeu Greco-Egipcíaca 377/120 = 3,141666... 23,56 ppm
263 Liu Hui Xina 3,14159 0,84 ppm
263 Wang Fan Xina 157/50 = 3,14 507 ppm
~300 Chang Hong Xina 101/2 ~ 3,1623 6584 ppm
~500 Zu Chongzhi Xina entre 3,1415926 y 3,1415929
usà 355/113 ~ 3,1415929		 <0,078 ppm
0,085 ppm
~500 Aryabhata Índia 3,1416 2,34 ppm
~600 Brahmagupta Índia 101/2 ~ 3,1623 6584 ppm
~800 Al-Khwarizmi Índia 3,1416 2,34 ppm
1116 Savasorda Catalana 377/120 = 3.141666.. 23,56 ppm
1220 Fibonacci Italiana 3,141818 72,73 ppm
1400 Madhava Índia 3,14159265359 0,085 ppm
1424 Al-Kashi Persa 2π = 6,2831853071795865 0,1 ppm
1585 Metius Holandesa 355/113 = 3,1415929203.. 0,085 ppm

[edita] Aproximacions emprant ordinadors

Any Descobridor Ordenador emprat Nombre de xifres decimals
1949 G.W. Reitwiesner i altres[25] ENIAC 2.037
1954   NORAC 3.092
1959 Guilloud IBM 704 16.167
1967   CDC 6600 500.000
1973 Guillord i Bouyer[25] CDC 7600 1.001.250
1981 Miyoshi i Kanada[25] FACOM M-200 2.000.036
1982 Guilloud   2.000.050
1986 Bailey CRAY-2 29.360.111
1986 Kanada i Tamura[25] HITAC S-810/20 67.108.839
1987 Kanada, Tamura, Kobo i altres NEC SX-2 134.217.700
1988 Kanada i Tamura Hitachi S-820 201.326.000
1989 Germans Chudnovsky CRAY-2 y IBM-3090/VF 480.000.000
1989 Germans Chudnovsky IBM 3090 1.011.196.691
1991 Germans Chudnovsky   2.260.000.000
1994 Germans Chudnovsky   4.044.000.000
1995 Kanada i Takahashi HITAC S-3800/480 6.442.450.000
1997 Kanada i Takahashi Hitachi SR2201 51.539.600.000
1999 Kanada i Takahashi Hitachi SR8000 68.719.470.000
1999 Kanada i Takahashi Hitachi SR8000 206.158.430.000
2002 Kanada i altres[25] [1] Hitachi SR8000/MP 1.241.100.000.000
2004 Hitachi 1.351.100.000.000

[edita] Primeres mil xifres del nombre pi

Aquestes són les primeres mil xifres del nombre pi:[26]

3,

1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989

[edita] Propietats

[edita] Irracionalitat

Article principal: Demostració de què π és irracional

El 1761 Johann Heinrich Lambert va demostrar que π és irracional. [3] Això vol dir que és un nombre real que no es pot expressar com a quocient de dos nombres enters. Al segle XX es van trobar demostracions que no necessiten coneixments que vagin mès enllà del càlcul integral. Una d'aquestes demostracions, la deguda a Ivan Niven, és amplament coneguda.[27][28] Una demostració similar lleugerament anterior la va obtenir Mary Cartwright.[29]

[edita] Transcendència

A més, π també és un nombre transcendent, tal com ho va demostrar Ferdinand von Lindemann el 1882. Això vol dir que no hi ha cap polinomi amb coeficients racionals tal que π sigui una de les seves arrels.[30] Una conseqüència important del fet de què π sigui transcendent és que no és construïble. Com que les coordenades de tots els punts que es poden construir amb regle i compàs són nombres constructibles, és impossible de quadrar el cercle: és a dir, és impossible, fent servir només compàs i regle, construïr un quadrat tal que la seva àrea sigui igual que l'àrea d'un cercle donat. [31] Històricament, això és significatiu, donat que la quadratura del cercle és un dels problemes fàcils d'entendre de geometria elemental que van quedar pendents de resoldre de l'antiguitat.

[edita] Questions obertes

La qüestió oberta més estudiada sobre π és si és o no un nombre normal—si qualsevol successió de xifres de l'expressió de π es dóna amb la freqüència que s'esperaria d'una successió completament "aleatòria", i si això és cert en qualsevol base, no només en base 10.[32] El que se sap actualment d'aquest tema és molt feble; és a dir ni tan sols se sap si algun dels dígits 0,…,9 apareix infinites vegades en l'expressió decimal de π.[33]

Bailey i Crandall van demostrar l'any 2000 que l'existència de la fórmula de Bailey-Borwein-Plouffe (Fórmula que permet calcular directament qualsevol xifra de l'expressió decimal de pi sense haver de calcular primer les xifres anteriors) implica que la normalitat en base 2 de π i de unes quantes constants més es pot reduir a una conjectura plausible de la teoria del caos.[34]

Tampoc se sap si π i e són algebraicament independents, tot i que Yuri Nesterenko va demostrar la independència algebraica de {π, eπ, Γ(1/4)} el 1996.[35]

[edita] Aplicacions en matemàtiques i física

Article principal: Llista de fórmules amb π

π apareix a tot arreu en matemàtiques, fins i tot en llocs on no hi ha cap connexió obvia amb les circumferències de la geometria euclidiana.[36]

[edita] Geometria i trigonometria

Vegeu també: Àrea del cercle

Per a qualsevol circumferència amb radi r i diàmetre d = 2r, el perímetre és πd i l'àrea és πr2. A més, π apareix en fórmules d'àrees i volums de moltes altres formes geomètriques basades en circumferències, com el·lipses, esferes Cons, i torus.[37] En conseqüència, π apareix en les integrals definides que calculen el perímetre, l'àrea o el volum de formes generades per circumferències. En el cas mé elementsl, la meitat de l'àrea del cercle de radi unitat ve donat per:[38]

\int_{-1}^1 \sqrt{1-x^2}\,dx = \frac{\pi}{2}

i

\int_{-1}^1\frac{1}{\sqrt{1-x^2}}\,dx = \pi

dóna la meitat del perímetre de la circumferència de radi unitat.[37] Formes geomètriques més complicades es poden integrar com sòlids de revolució.[39]

A partir de la definició de les funcions trigonomètriques basada en la circumferència goniomètrica resulta que el sinus i el cosinus tenen el període 2π (si l'angle s'expressa en radians). És a dir, per a tot x real i tot n enter, sin(x) = sin(x + 2πn) i cos(x) = cos(x + 2πn). Com que sin(0) = 0, sin(2πn) = 0 per a tot n enter. També, la mesura de l'angle de 180 ° és igual a π radians. En altres paraules, 1 ° = (π/180) radians.

[edita] Nombres complexos i càlcul infinitesimal

Euler's formula.svg

L'aparició freqüent de π en l'anàlisi complexa es pot relacionar amb el comportament de la funció exponencial de variable complexa, que descriu la fórmula d'Euler

e^{i\varphi} = \cos \varphi + i\sin \varphi \!

on i és la unitat imaginària que satisfà i2 = −1 i e ≈ 2.71828 és el nombre d'Euler. Aquesta fórmula implica que les potències imaginaries d' e descriuen rotacions en la circumferència goniomètrica en el pla complex; aquestes rotacions tenen un període de 360 ° = 2π. En particular, la rotació de 180 ° φ = π ocasiona la notable identitat d'Euler

e^{i \pi} = -1.\!

Hi ha n arrels de la unitat n-èssimes diferents

e^{2 \pi i k/n} \qquad (k = 0, 1, 2, \dots, n - 1).

La Integral de Gauß

\int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{\pi}.

Una conseqüència és que la funció gamma de la meitat d'un enter és un míltiple racional de √π.

[edita] Física

Encara que no una constant física, π apareix freqüentment en equacions que descriuen principis fonamentals de l'Univers, degut en gran part a la seva relació amb la circumferència, i en conseqüència amb els sistemes de coordenades esfèriques. Fent servir unitats com ara les Unitats de Planck a vegades poden eliminar de π fórmules.

\Lambda = {{8\pi G} \over {3c^2}} \rho
\Delta x\, \Delta p \ge \frac{h}{4\pi}
R_{ik} - {g_{ik} R \over 2} + \Lambda g_{ik} = {8 \pi G \over c^4} T_{ik}
F = \frac{\left|q_1q_2\right|}{4 \pi \varepsilon_0 r^2}
\mu_0 = 4 \pi \cdot 10^{-7}\,\mathrm{N/A^2}\,
\frac{P^2}{a^3}={(2\pi)^2 \over G (M+m)}

[edita] Probabilitat i estadística

En probabilitat i estadística, hi ha moltes distribucions de probabilitat les fórmules de les quals contenen π, per exemple:

f(x) = {1 \over \sigma\sqrt{2\pi} }\,e^{-(x-\mu )^2/(2\sigma^2)}
f(x) = \frac{1}{\pi (1 + x^2)}.

Fixeu-vos que com que \int_{-\infty}^{\infty} f(x)\,dx = 1 per totes les funcions densitat de probabilitat f(x), les fórmules anteriors es poden fer servi per obtenir altres fórmules integrals on intervé π.[47]

El problema de les agulles de Buffon s'esmenta de vegades com a aproximació empírica de π. Es tracta de deixar caure una agulla de la llargada L repetidament sobre una superfície que conté línies paral·leles dibuixades separades entre elles a S (amb S > L). Si l'agulla es deixa caure n vegades i x d'aquestes vegades cau creuant una línia (x > 0), llavors es pot aproximar π fent servir el mètode de Monte Carlo:[48][49][50][51]

\pi \approx \frac{2nL}{xS}.

Encara que aquest resultat és matemàticament impecable, no es pot fer servir per determinar més que molt pocs dígits de π experimentalment. Obtenir de manera fiable només tres dígits (incloent-hi l'inicial "3") exigeix milions de tirades,[48] i el nombre de llançaments augmenta exponencialment amb el nombre de dígits desitjats. A més, qualsevol error en la mesura de les llargades L i S es transferirà directament a un error en l'aproximació de π. Per exemple, una diferència d'un únic àtom en la llargada d'una agulla de 10 centímetres apareixeria al voltant del 9è dígit del resultat. En la pràctica, les incerteses de determinar si l'agulla de fet creua una línia quan sembla tocar-la exactament, limitaran la precisió realitzable a molt menys de 9 dígits.

[edita] Referències culturals i curiositats

mosaic que representa π a l'entrada de l'edifici de matemàtiques de la Universitat Tècnica de Berlín.
  • El valor 3,2 pel nombre π va estar a punt de ser imposat per llei a l'estat d'Indiana. Es va tramitar el projecte de llei 246 de 1897 a instàncies del matemàtic aficionat Edward J. Goodwin que reivindicava haver trobat el mètode de la quadratura del cercle. El projecte de llei va obtenir l'informe favorable del comitè d'educació. La aprovació es va posposar degut a la intervenció del professor de matemàtiques C. A. Waldo que accidentalment estava de visita. Actualment la tramitació de la llei encara no s'ha completat i continua pendent d'aprovació. [52]
  • A Argentina, el nombre telefònic mòbil per emergències en estacions de trens i soterranis és el nombre Pi: 3,1416.[53]
  • Hi ha in vehicle Mazda 3 modificat, al que se li van afegir 27 xifres de π, desprès del 3.[54]
  • Els anomenats piemes són poemes composats de forma que el nombre de lletres de les successives paraules coincideixin amb les xifres del nombre pi, per exemple el següent poema: Ell i ella, l'única esperança de tindre fills que tenen, romandrà soterrada aquesta primavera. Fixeu-vos que la primera paraula té 3 lletres, la segona 1 i així successivament s'obtenen les xifres: 3,14159265358979 La Cadaeic Cadenza és un llibre que conté les primeres 3834 xifres de π d'aquesta forma.[55]
  • Desde molt abans que els ordinadors permetessin calcular gran quantitat de xifres de π, memoritzar una quantitat rècord d'aquestes xifres esdevingué una obsessió per algunes persones. El 2006, Akira Haraguchi, un enginyer japonès retirat, va reivindicar haver recitat 100,000 xifres decimals.[56] Però això no ha estat verificat encara pel llibre Guinness dels rècords. El record reconegut pel Guinness de memorització de xifres de π és 67,890 xifres, i el té Lu Chao, un estudiant xinès graduat de 24 anys.[57] Va trigar 24 hores i 4 minuts per recitar fins al 67,890è decimal de π sense cap error.[58]
  • Darrerament s'han fet simfonies basades en diferents constants matemàtiques, assignant a cada nombre decimal una determinada nota. [59]
  • Si π és un nombre normal, és natural trobar en els decimals de π qualsevol seqüència de nombres, encara que de vegades alguna sigui sorprenent.Jean-Paul Delahaye [60] assenyala per exemple que la suma dels 20 primers decimals de π dóna 100 i que la suma dels 144 primers decimals dóna 666 però precisa que no cal veure-hi cap missatge amagat. Altres autors tanmateix són menys prudents. Així Robert Gold, aficionat a la geometria, afirma haver trobat, amb l'ajuda de càlculs complicats, que les paraules claus de la Bíblia estan a π.[61]

[edita] Referències

  1. ↑ Beckmann, Petr. A History of π. St. Martin's Griffin, 1976. ISBN 0-312-38185-9. 
  2. ↑ «Archimedes' constant π». [Consulta: 2007-11-04].
  3. ↑ 3,0 3,1 3,2 3,3 3,4 «About Pi». Ask Dr. Math FAQ. [Consulta: 2007-10-29].
  4. ↑ Aleff, H. Peter. «Ancient Creation Stories told by the Numbers: Solomon's Pi». recoveredscience.com. [Consulta: 2007-10-30].
  5. ↑ 5,0 5,1 5,2 O'Connor, J J; E F Robertson. «A history of Pi», 2001-08. [Consulta: 2007-10-30].
  6. ↑ Smith DE. The Teaching of Geometry, 1911, 279. 
  7. ↑ Llibre de Geometria Savasorda, pàgina XV.
  8. ↑ Wilbur Richard Knorr, The Ancient Tradition of Geometric Problems, New York: Dover Publications, 1993.
  9. ↑ Ramon Llull al s. XXI Actes de les Jornades Internacionals Lul·lianes, Palma, 1, 2 i 3 d'abril de 2004 Col·lecció Blaquerna Edicions Universitat Barcelona, 2005 ISBN 8476329431, 9788476329436, pàgina 113
  10. ↑ George E. Andrews, Richard Askey, Ranjan Roy (1999), Special Functions, Cambridge University Press, p. 58, ISBN 0521789885
  11. ↑ Gupta, R. C. (1992), "On the remainder term in the Madhava-Leibniz's series", Ganita Bharati 14 (1-4): 68–71
  12. ↑ Charles Hutton. Mathematical Tables; Containing the Common, Hyperbolic, and Logistic Logarithms.... London: Rivington, 1811, p.13. 
  13. ↑ The New York Times: Even Mathematicians Can Get Carried Away
  14. ↑ «About: William Jones». Famous Welsh. [Consulta: 2007-10-27].
  15. ↑ 15,0 15,1 «The constant π: Ramanujan type formulas». [Consulta: 2007-11-04].
  16. ↑ Brent, Richard (1975), Traub, J F, ed., "Multiple-precision zero-finding methods and the complexity of elementary function evaluation", Analytic Computational Complexity (New York: Academic Press): 151–176, <http://wwwmaths.anu.edu.au/~brent/pub/pub028.html>. Consultat el 8 setembre 2007
  17. ↑ Borwein, Jonathan M; Borwein, Peter, Berggren, Lennart. Pi: A Source Book. Springer, 2004. ISBN 0387205713. 
  18. ↑ 18,0 18,1 Bailey, David H., Borwein, Peter B., and Plouffe, Simon. «On the Rapid Computation of Various Polylogarithmic Constants» (PDF). Mathematics of Computation, vol. 66, 218, pàg. 903–913.
  19. ↑ Bellard, Fabrice. «A new formula to compute the nth binary digit of pi». [Consulta: 2007-10-27].
  20. ↑ Vegeu Proposició 20 del llibre VI dels elements d'Euclides
  21. ↑ Richmond, Bettina. «Area of a Circle». Western Kentucky University, 1999-01-12. [Consulta: 2007-11-04].
  22. ↑ Proposició 2 del Llibre XII dels Elements d'Euclides
  23. ↑ Rudin, Walter [1953]. Principles of Mathematical Analysis, 3e. McGraw-Hill, 1976, 183. ISBN 0-07-054235-X. 
  24. ↑ Pi continued fraction representations (13 formulas) representació de &pi en fraccions contínues a WolframResearch
  25. ↑ 25,0 25,1 25,2 25,3 25,4 Bailey David H. , Some Background on Kanada’s Recent Pi Calculation (2003). Disponible en aquest enllaç. Consultada:22 d'abril de 2008
  26. ↑ Primers 1.250.000 dígits del nombre π
  27. ↑ Niven, Ivan. «A simple proof that π is irrational» (PDF). Bulletin of the American Mathematical Society, vol. 53, pàg. 509 [Consulta: 2007-11-04].
  28. ↑ Richter, Helmut. «Pi Is Irrational». Leibniz Rechenzentrum, 1999-07-28. [Consulta: 2007-11-04].
  29. ↑ Jeffreys, Harold. Scientific Inference, 3rd. Cambridge University Press, 1973. 
  30. ↑ Mayer, Steve. «The Transcendence of π». [Consulta: 2007-11-04].
  31. ↑ «Squaring the Circle». cut-the-knot. [Consulta: 2007-11-04].
  32. ↑ Weisstein, Eric W. «Normal Number». MathWorld, 2005-12-22. [Consulta: 2007-11-10].
  33. ↑ Preuss, Paul (2001-07-23). "Are The Digits of Pi Random? Lab Researcher May Hold The Key", Lawrence Berkeley National Laboratory. Revisat el 10 novembre 2007. 
  34. ↑ Peterson, Ivars (2001-09-01). "Pi à la Mode: Mathematicians tackle the seeming randomness of pi's digits", Science News Online. Revisat el 10 novembre 2007. 
  35. ↑ Nesterenko, Yuri V. «Modular Functions and Transcendence Problems». Comptes rendus de l'Académie des sciences Série 1, vol. 322, pàg. 909–914.
  36. ↑ «Japanese breaks pi memory record». BBC News, 2005-07-02. [Consulta: 2007-10-30].
  37. ↑ 37,0 37,1 «Area and Circumference of a Circle by Archimedes». Penn State. [Consulta: 2007-11-08].
  38. ↑ Weisstein, Eric W. «Unit Disk Integral». MathWorld, 2006-01-28. [Consulta: 2007-11-08].
  39. ↑ Weisstein, Eric W. «Solid of Revolution». MathWorld, 2006-05-04. [Consulta: 2007-11-08].
  40. ↑ Miller, Cole. «The Cosmological Constant» (PDF). University of Maryland. [Consulta: 2007-11-08].
  41. ↑ Imamura, James M. «Heisenberg Uncertainty Principle». University of Oregon, 2005-08-17. [Consulta: 2007-11-09].
  42. ↑ Einstein, Albert. «The Foundation of the General Theory of Relativity» (PDF). Annalen der Physik [Consulta: 2007-11-09].
  43. ↑ Nave, C. Rod. «Coulomb's Constant». HyperPhysics. Georgia State University, 2005-06-28. [Consulta: 2007-11-09].
  44. ↑ «Magnetic constant». NIST, 2006 CODATA recommended values. [Consulta: 2007-11-09].
  45. ↑ Weisstein, Eric W. «Gaussian Integral». MathWorld, 2004-10-07. [Consulta: 2007-11-08].
  46. ↑ Weisstein, Eric W. «Cauchy Distribution». MathWorld, 2005-10-11. [Consulta: 2007-11-08].
  47. ↑ Weisstein, Eric W. «Probability Function». MathWorld, 2003-07-02. [Consulta: 2007-11-08].
  48. ↑ 48,0 48,1 Weisstein, Eric W. «Buffon's Needle Problem». MathWorld, 2005-12-12. [Consulta: 2007-11-10].
  49. ↑ Bogomolny, Alex. «Math Surprises: An Example». cut-the-knot, 2001-08. [Consulta: 2007-10-28].
  50. ↑ Ramaley, J. F.. «Buffon's Noodle Problem». The American Mathematical Monthly, vol. 76, 8, pàg. 916–918.
  51. ↑ «The Monte Carlo algorithm/method». datastructures, 2007-01-09. [Consulta: 2007-11-07].
  52. ↑ "Indiana's squared circle" , Arthur E. Hallerberg (Mathematics Magazine, vol. 50 (1977), pp. 136-140) dóna una bona explicació del projecte de llei.
  53. ↑ http://www.mininterior.gov.ar/camarasenvivo/inicio.asp
  54. ↑ "Mazda Pi" en Gaussianos.com. Consultado: 23 de abril de 2008
  55. ↑ Keith, Mike. «Cadaeic Cadenza: Solution & Commentary», 1996. [Consulta: 2007-10-30].
  56. ↑ Otake, Tomoko (2006-12-17). "How can anyone remember 100,000 numbers?", The Japan Times. Revisat el 27 octubre 2007. 
  57. ↑ «Pi World Ranking List». [Consulta: 2007-10-27].
  58. ↑ "Chinese student breaks Guiness record by reciting 67,890 digits of pi", News Guangdong (2006-11-28). Revisat el 27 octubre 2007. 
  59. ↑ Pisymphony (anglès) pàgina on es troben simfonies basades en el nombre π i e.
  60. ↑ Conférence de Jean-Paul Delahaye, le nombre pi est-il simple ou compliqué consultable ici
  61. ↑ Robert Gold, "Dieu et le nombre pi", Éditions O. Bène Kénane, ISBN 9652227277


[edita] Vegeu també

[edita] Bibliografia

[edita] Enllaços externs

Commons-logo.svg
 A Wikimedia Commons hi ha contingut multimèdia relatiu a:
Nombre π
Viquipèdia:Llista d'articles que totes les llengües haurien de tenir#Ciències naturals

Obtingut de «http://ca.wikipedia.org/wiki/Nombre_%CF%80»