Estadística

L'estadística o estatística[1] és la disciplina de la ciència relacionada amb la recopilació, anàlisi, interpretació i representació de dades. S'utilitza en diverses disciplines acadèmiques, de les ciències físiques a les ciències socials i humanitats. A l'enginyeria l'estadística aplicada s'utilitza sobretot per a obtenir resultats empírics i per al control de la qualitat i de lleis i normatives. També s'utilitza en la presa informada de decisions en les diverses àrees dels negocis i del govern.[2]
Els mètodes estadístics s'utilitzen per resumir o descriure un grup de dades; això s'anomena estadística descriptiva. A més, els patrons de les dades es poden modelar considerant l'aleatorietat i la incertesa de les observacions per tal d'inferir quant al procés o la població que es vol estudiar; això s'anomena estadística inferencial o inductiva. L'estadística descriptiva i l'estadística inferencial són part de l'estadística aplicada.[3][4][5] També existeix l'estadística matemàtica que estudia els conceptes teòrics de la disciplina.
L'estadística és la pràctica de desenvolupar coneixement humà mitjançant l'ús de dades empíriques. Es basa en la teoria estadística, que és una branca de la matemàtica aplicada. Seguint aquesta teoria, la incertesa i l'aleatorietat es modelen utilitzant la teoria de probabilitats. La pràctica de l'estadística inclou la planificació, resum i interpretació d'observacions incertes. Com que l'objectiu de l'estadística és produir la millor informació amb la informació disponible, alguns autors la consideren una branca de la teoria de decisions.
Història[modifica]
Si bé el nom d'estadística és relativament recent – en general s'atribueix l'origen del nom al segle xviii de l'alemany Staatskunde (coneixement d'estat) – aquesta activitat sembla que ha existit des del naixement de les primeres estructures socials. D'altra banda, els primers texts escrits que s'han trobat eren censos de bestiar, informacions sobre el seu curs i contractes diversos. Es té així rastre de censos a la Xina al segle XXIII aC o a Egipte al segle XVIII aC. Aquest sistema de recull de dades prossegueix fins al segle xvii. A Europa, el paper de col·lector és sovint mantingut per gremis comercials, i després pels intendents de l'Estat. És només al segle xviii que es veu aparèixer el paper preventiu de les estadístiques amb la construcció de les primeres taules de mortalitat.
L'estadística matemàtica es va recolzar en els primers treballs en relació amb les probabilitats desenvolupats per Fermat i Pascal. És probablement amb Thomas Bayes que es viu aparèixer un embrió d'estadística inferencial. Condorcet i Laplace encara parlaven de probabilitat allà on avui es parlaria de freqüència. Però és a Adolphe Quételet a qui es deu la idea que l'estadística és una ciència que es recolza en les probabilitats.
Al segle xix aquesta activitat pren el seu desenvolupament ple. Es van promulgar regles precises sobre la recol·lecció i la interpretació de les dades. La primera aplicació industrial de les estadístiques va tenir lloc en el moment del padró americà de 1890, que va fer servir la targeta perforada inventada per l'estadístic Herman Hollerith. Aquest havia dipositat una patent a l'Oficina de patents dels Estats Units.
Al segle xx, aquestes aplicacions industrials es van desenvolupar en principi als Estats Units, que anaven avançats en ciències de gestió, i només després de la Primera guerra mundial a Europa. El règim nazi va fer servir mètodes estadístics a partir de 1934 per al rearmament.
A Catalunya, el Servei Central d'Estadística va ser creat per la Generalitat el 1934 i dirigit per Josep Anton Vandellós i Solà, catedràtic d'Estadística de la Universitat de Barcelona.[6]
L'adveniment de la informàtica en els anys 1940 (als Estats Units), i després a Europa (en els anys 1960) va permetre tractar més dades, però sobretot creuar sèries de dades de tipus diferents entre elles. És el desenvolupament del que s'anomena l'anàlisi multidimensional. En el transcurs del segle, apareixen diversos corrents de pensament enfrontats:
- els objectivistes o freqüentistes que pensen que les probabilitats subministren un model que permet idealitzar la distribució en freqüència i que aquí s'acaba el seu paper;
- els subjectivistes que veuen les probabilitats com un mitjà per mesurar la confiança que es pot tenir en una previsió;
- els neobayesianistes que sostenen que les dades estadístiques soles no permeten donar el model probabilista idealitzant la distribució en freqüència: és necessari proposar una forma general del model per ajustar-hi el resultat.
Visió general[modifica]
En aplicar l'estadística a un problema científic, industrial o de la societat, es comença estudiant el procés o la població. La població es pot referir literalment als habitants d'un país, o al nombre de grans de cristall d'una roca, o als béns manufacturats per una fàbrica especial durant un període determinat de temps. També pot referir-se al procés d'observacions en diversos períodes; les dades d'aquesta "població" conformen una sèrie de temps o sèrie temporal.
Per exemple en les notes globals d'un examen. Pot ser interessant treure'n un valor central que dona una idea sintètica sobre el nivell dels estudiants. Aquesta informació es pot completar amb un valor de dispersió que mesura, d'una certa manera, l'homogeneïtat del grup. Si es vol una informació més precisa sobre aquest últim punt, es pot construir un histograma o, des d'un punt de vista lleugerament diferent, considerar els decils. Aquestes nocions poden ser interessants per fer comparacions amb els exàmens anàlegs passats els anys precedents o en altres llocs. Són els problemes més elementals de l'anàlisi de les dades que afecten a una població finita.
Per raons pràctiques, en comptes de recollir dades de tota la població, sovint només s'estudia un subconjunt de la població, anomenat "mostra". De vegades la població és infinita (com per exemple en el cas dels instants del temps en què es pot produir una avaria) o pel fet de ser molt gran es fan servir les fórmules matemàtiques corresponents a una població infinita. Les dades s'obtenen en un experiment o observació. Les dades, després, s'analitzen estadísticament, amb el propòsit de descriure i d'inferir:
- L'estadística descriptiva resumeix les dades de manera útil, numèricament o gràficament (p.e. la tendència central: mitjana, mitjana ponderada, etc.) L'estadística descriptiva, en aquest cas, descriu només la mostra.
- L'estadística inferencial o inductiva s'utilitza per a modelar els patrons de les dades de la mostra i inferir sobre les característiques de tota la població. Per induir informacions sobre la població desconeguda a partir de les informacions de la mostra, cal introduir la noció de llei de probabilitat. Les dades conegudes constitueixen en aquest cas una realització d'una mostra, conjunt de variables aleatòries que es creuen independents (veure Llei de probabilitat amb diverses variables). La teoria de la probabilitat permet, llavors, treure conclusions (o inferir) relatives a la població a partir de les dades de la mostra. Les inferències poden ser proves d'hipòtesi, estimacions, prediccions de les observacions futures, descripcions d'associació (correlació), o la descripció de la relació entre variables (regressió). Altres tècniques són l'ANOVA (Anàlisi de Variància), les sèries temporals i la mineria de dades.
Si la mostra és representativa en relació amb la població, les inferències i les conclusions de la mostra es poden estendre a la població total (procés d'inducció). Un problema important d'estadística és la determinació d'una mostra representativa. L'estadística ofereix mètodes per estimar o corregir l'aleatorietat (incertesa) de la mostra així com de la recopilació de dades. Per a entendre aquesta incertesa, es fa servir el concepte matemàtic de la probabilitat. L'estadística matemàtica (o teoria estadística), com a branca de la matemàtica aplicada, fa servir la teoria de la probabilitat per analitzar i examinar els conceptes teòrics bàsics de l'estadística.
Parts de l'estadística[modifica]
Recollida de dades[modifica]

L'enquesta estadística (preguntes, enquestes o qüestionaris) sempre ve precedida d'una fase on es determinen els diferents aspectes a estudiar.
L'etapa següent consisteix a escollir la població a estudiar. Llavors es planteja el problema del mostreig: tria de la població a sondejar (en sentit ampli: pot ser un sondeig d'opinió d'una població humana, o bé la recollida de roques per determinar la naturalesa d'un sòl en geologia), la talla de la població i la seva representativitat.
Les idees fonamentals del disseny d'experiments són: Comparació entre experiments a banda de mesura directa. Selecció aleatòria dels elements amb els quals fer l'experiment. Replicació tant per mesures repetides com per replicació del mateix experiment. Agrupació de diversos experiments similars en un per tal de reduir la variabilitat. Ortogonalitat entre els paràmetres d'estudi. A més en alguns casos en comptes d'estudiar l'efecte de cada factor un per un, convé més dissenyar experiments factorials en què s'estudien simultàniament diversos factors.
Vegeu:
Ja sigui per a una mostra total (padró) o parcial (sondeig), s'han d'establir protocols per evitar els errors de mesures tant els accidentals com els sistemàtics (biaix).
El tractament previ de les dades és extremadament important, en efecte, una transformació de les dades inicials (un pas al logaritme, per exemple), pot facilitar considerablement els tractaments estadístics següents.
Tractament de les dades[modifica]
El resultat de l'enquesta estadística és una sèrie de dades numèriques (edat, talles, salaris) o de dades qualitatives (gènere, característiques físiques, llengües parlades, marques preferides). Per poder explotar-les, cal fer-ne una classificació i un resum visual o numèric mitjançant, per exemple, taules de freqüències, gràfics de barres o gràfics circulars. De vegades, quan tenim un nombre de dades diferents molt gran, és necessari efectuar una compressió de dades, agrupant aquestes en intervals. Aquesta és la feina de l'estadística descriptiva. Serà diferent segons si l'estudi es basa sobre una sola variable o sobre diverses variables.
Estudi d'una sola variable[modifica]
L'agrupament de dades, el càlcul de les quantitats, la construcció de gràfics permet obtenir un primer resum visual de la variable estadística estudiada. En el cas d'una variable quantitativa contínua, l'histograma n'és la representació gràfica més corrent. En aquest tipus de gràfic, cada grup es representa amb un rectangle i tindrà la mateixa amplada que el seu interval i una altura proporcional a la seva freqüència. El polígon de freqüències és una altra manera de representar les dades agrupades. En aquest cas, el creem en unir els extrems superiors de les barres dels histogrames o dels diagrames de barres.
-
(A) Un conjunt aleatori de punts
-
(B) Un histograma associat
-
(C) La funció distribució de probabilitat teòrica (vermell) i l'empírica (negre)
Els valors numèrics d'una variable estadística es reparteixen en , cal definir les seves posicions. En estadística, hi ha presència d'un gran nombre de valors. Ara bé, si la totalitat d'aquests valors conforma la informació, no és fàcil manipular diversos centenars i fins i tot milers de dades, ni treure'n conclusions. Cal doncs calcular alguns valors que permetran analitzar les dades. Aquests poden ser extremadament concisos, reduïts a un nombre: és el cas dels valors centrals i dels valors de dispersió. Alguns (com ara la variància) es van desenvolupar per permetre una explotació més teòrica de les dades (vegeu Inferència estadística)
També es pot intentar comparar dues poblacions. L'interès se centra llavors més particularment en els seus criteris de posició, de dispersió, el seu diagrama de caixa o l'anàlisi de la variància.
Estudi de diverses variables[modifica]
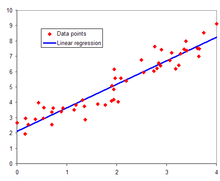
Avui en dia, els mitjans informàtics permeten estudiar diverses variables simultàniament. El cas de dues variables donarà lloc a la creació d'un núvol de punts, i un eventual estudi de correlació entre els dos fenòmens o l'estudi d'una regressió lineal.
Però es poden fer estudis sobre més de dues variables: és l'anàlisi multidimensional en el qual es troba l'anàlisi de components principals, l'anàlisi de components independents, la regressió lineal múltiple i la mineria de dades. Avui en dia, la mineria de dades es recolza en l'estadística per descobrir relacions entre les variables de bases de dades molt grans. Els avenços tecnològics (augment de la freqüència dels sensors disponibles, els mitjans d'emmagatzematge, i de la potència de càlcul) augmenten l'interès per la mineria de dades.
Interpretació i anàlisi de les dades[modifica]

La diferència estadística té per objectiu induir les propietats d'una població a partir dels resultats obtinguts amb una mostra.
Es recolza en els resultats de l'estadística matemàtica, que aplica càlculs matemàtics rigorosos basats en la teoria de la probabilitats i en la teoria de la informació a les situacions on no s'observen més que algunes mostres (experiments) del fenomen a estudiar.
Sense l'estadística matemàtica, un càlcul sobre les dades (per exemple una mitjana), no és més que un indicador. És l'estadística matemàtica que li dona l'estatus d'estimador del qual se'n determinen el biaix, la incertesa i altres característiques estadístiques. En general es busca que l'estimador sigui sense baix, convergent i eficaç.
També es poden emetre hipòtesis sobre la llei que genera el fenomen general, per exemple «la talla dels nens de 10 anys als Països Catalans segueix una distribució normal?». Llavors l'estudi de la mostra validarà o no aquesta hipòtesi: que s'anomena el contrast d'hipòtesis. Les proves d'hipòtesis permeten quantificar la probabilitat amb la qual variables (conegudes només a partir d'una mostra) verifiquen una propietat donada.
Finalment, es pot intentar modelitzar un fenomen a posteriori. La modelització estadística s'ha de distingir de la modelització física. En el segon cas els físics (també els químics, biòlegs, qualsevol científic), intenten construir un model explicatiu d'un fenomen, que se sostingut per una teoria més general descrivint com es produeixen els fenòmens emprant el principi de causalitat. En el cas de la modelització estadística, el model es construirà a partir de les dades disponibles, sense cap a priori sobre els mecanismes que entren en joc. Aquest tipus de modelització també es diu modelització empírica. Sempre és positiu completar una modelització estadística amb equacions físiques (sovint integrades dins del tractament previ de les dades).
Un model és abans de tot un mitjà de connectar les variables a explicar Y amb les variables explicatives X, per una relació funcional:
Els models estadístics es poden ser classificar en grans famílies (segons la forma de la funció F):
- models lineals;
- models no lineals;
- models no paramètrics.
Els models bayesians (del nom de Bayes) es poden fer servir en les tres categories.
Estadística matemàtica[modifica]
Aquesta branca de les matemàtiques, molt vinculada a les probabilitats, és indispensable per validar les hipòtesis o els models elaborats en l'estadística inferencial. La teoria matemàtica de les probabilitats es formalitza en els fenòmens aleatoris. L'estadística matemàtica es dedica a l'estudi de fenòmens aleatoris que es coneixen via algunes de les seves ocurrències.
Per exemple, per a una partida de daus de sis cares:
- El punt de vista probabilístic és el de formalitzar aquest joc per una distribució de probabilitat associada als esdeveniments: ha sortit la primera, la segona..., la sisena cara. La teoria de les probabilitats diu per exemple que perquè aquesta distribució sigui una distribució de probabilitat, cal que . Llavors es poden estudiar diferents propietats d'aquest joc;
- una vegada establert això, llavors les estadístiques s'interessen per aquest gènere de qüestió: «Si al final de 100 partides, cada cara n ha sortit vegades, es pot tenir una idea del valor de les probabilitats ? Amb quin grau de confiança?»
Una vegada establerta la regla, es pot fer servir en estadística inferencial.
Aplicació dels ordinadors al càlcul estadístic[modifica]

El procés d'augment ràpid i sostingut de la potència de càlcul que es va començar a la segona meitat del segle xx ha tingut un impacte substancial en la ciència estadística. Els models estadístics, inicialment eren gairebé sempre del tipus dels models lineals, però la potència dels ordinadors acompanyada del desenvolupament d'algorismes de càlcul numèric adequats, ha provocat o ha augmentat l'interès en models no lineals (com ara les xarxes neurals) així com la creació de nous models, com ara el model lineal generalitzat els models multinivell.
L'augment de la potència de càlcul, també ha portat a l'augment de la popularitat dels mètodes intensius en càlcul basats en el remostreig, com ara els tests de permutacions i els bootstrapping, mentre que tècniques com ara el mostreig de Gibbs han fet ús de models Bayesians més factibles. La revolució informàtica té implicacions en el futur de l'estadística amb un nou èmfasi en l'estadística "experimental" i "empírica". Avui en dia hi ha disponible un gran nombre de paquets de programari estadístic tant de propòsit general com específic. Alguns dels més populars són l'SPSS, el PSPP o també els basats en el llenguatge de programació R.
Aplicació de l'estadística[modifica]
Les estadístiques es fan servir en àmbits molt variats com:
- en arqueologia, aplicada als vestigis;
- en biologia: aplicació dels mètodes estadístics en el camp de la biologia (Bioestadística);
- en ciències econòmiques i socials, i en econometria: l'estudi del comportament d'un grup de població o d'un sector econòmic es recolza en estadístiques. Les qüestions mediambientals es basen igualment en dades estadístiques;
- en demografia: el padró permet fer una fotografia en un instant donat d'una població i llavors permet fer sondatges amb mostres representatives;
- en ecologia (estudi de les comunitats vegetals i dels ecosistemes)
- en enginyeria s'usa per a la investigació, per a estudis de qualitat i d'excel·lència, entre altres coses;
- en física: l'estudi de la mecànica estadística i de la termodinàmica estadística (Física estadística) permet deduir del comportament de partícules individuals un comportament global (pas del microscòpic al macroscòpic);
- en geofísica, per a les previsions meteorològiques, la climatologia, la contaminació, els estudis dels rius i oceans;
- en màrqueting: el sondatge d'opinió esdevé una eina per a la decisió o la inversió;
- en medicina i en psicologia, tant per l'estudi del comportament de les malalties en la seva freqüència d'aparició o la validesa d'un tractament o d'un sistema de detecció;
- en metrologia, per tot el que concerneix als sistemes de mesura i les mesures mateixes;
- en sociologia: les fonts estadístiques constitueixen materials d'enquesta, i els mètodes estadístics es fan servir com tècniques de tractament de les dades.
Mal ús[modifica]
Hi ha una percepció generalitzada de què les estadístiques, amb massa freqüència es fan servir malament a base de trobar formes d'interpretar les dades només de la manera que afavoreixen a qui les presenta. Una dita famosa atribuïda a Benjamin Disraeli és, «Mentides, grans mentides i estadístiques|Hi ha tres classes de mentides: mentides, grans mentides i estadístiques». El president de Harvard Lawrence Lowell va escriure el 1909 que les estadístiques, "...com els pastissos de carn, són bones si es coneix qui les ha fet, i s'està segur dels ingredients."
Si sembla que diversos estudis es contradiuen, llavors el públic pot arribar a perdre la confiança en aquest tipus d'estudis. Per exemple, un estudi pot suggerir que una dieta o una activitat fa augmentar la pressió arterial, mentre que un altre pot suggerir que la fa baixar. La discrepància pot sorgir de variacions subtils en el disseny d'experiments, tals com diferències en grups de pacients o en protocols de recerca, les quals no s'entenen fàcilment pels no experts. (Els informes dels mitjans de comunicació, normalment ometen completament aquesta informació de context que és vital, degut a la seva complexitat.)
A còpia de triar (o rebutjar, o modificar) una determinada mostra, es poden manipular els resultats. Aquesta mena de manipulacions no han de ser necessàriament malintencionades; poden sorgir de biaixos sense voler de l'investigador. Els gràfics que es fan servir per resumir les dades també poden generar interpretacions confuses.
Les crítiques més profundes venen del fet que la metodologia per provar les hipòtesis que es fa servir més àmpliament (i en molts casos requerida per les regulacions legals) força que s'"afavoreixi" una hipòtesi (la hipòtesi nul·la) i en estudis grans també pot semblar que exagera la importància de diferències minúscules. Una diferència que resulti altament significativa estadísticament pot resultar pràcticament insignificant. (Vegeu crítiques a les proves d'hipòtesi i controvèrsia sobre la hipòtesi nul·la.)
Una resposta és donar més èmfasi al valor p que no pas només informar de quan una hipòtesi es rebutja a un nivell de significació. Però el valor p no indica la mida de l'efecte. Un altre enfocament cada vegada més comú és informar dels intervals de confiança. Encara que s'obtenen a partir dels mateixos càlculs que els dels tests d'hipòtesis o valors p, descriuen tant la mida de l'efecte com la incertesa que l'envolta.
Aplicació de l'estadística a la recerca matemàtica i l'art[modifica]
Tradicionalment l'estadística s'ha fet servir per fer inferències sobre les característiques d'una població a partir de les característiques d'una mostra. Això ha canviat amb l'ús dels mètodes desenvolupats per l'estadística en contextos no inferencials.
- Punts aleatoris de dades generats per una funció de distribució es poden transformar amb tècniques que fa servir l'estadística per revelar patrons subjacents, els quals poden conduir a fer hipòtesis, per exemple en teoria de nombres.
- Mètodes de la ciència estadística incloent-hi mètodes predictius en previsió, es combinen amb la teoria del caos i la geometria fractal per crear obres de vídeo que es considera que són boniques. El process art de Jackson Pollock descansa en experiments artístics on les distribucions subjacents a la natura es revelen de forma artística. Amb l'adveniment dels ordinadors, s'han aplicat els mètodes estadístics per formalitzar aquestes distribucions conduïdes per processos naturals, amb la finalitat de fer i analitzar art en vídeo en moviment.
- Els mètodes estadístics es poden fer servir de forma predictiva, no inferencial, en arts escèniques, com en els trucs de cartes basats en els processos de Markiov que només funcionen algunes vegades, per mitjà de fer prediccions emprant la metodologia estadística.
- L'estadística es fa servir per crear art de forma predictiva, per exemple en aplicacions de mecànica estadística amb música estadística o estocàstica inventada per Iannis Xenakis, on la música és específica de cada actuació, i no sempre resulta tal com s'esperava, però ho fa dins d'un interval predit fent servir estadística.
Bibliografia[modifica]
- Métodos estadísticos. Volum I. Albert Prat i Bartés, Xavier Tort-Martorell i Llobés, Pere Grima i Cintas, Lourdes Pozueta i Fernández. Edicions UPC. 1997 ISBN 84-8301-222-7
- Fortiana, J.; Nualart, D. Estadística (en català). 1. Barcelona: Edicions de la Universitat de Barcelona, 1999, p. 110. ISBN 84-8338-093-5.
Referències[modifica]
- ↑ Estatística. Bibiloni
- ↑ «statistics | Definition, Types, & Importance | Britannica» (en anglès). [Consulta: 14 febrer 2022].
- ↑ «Estadística - Definición, qué es y concepto» (en castellà). [Consulta: 18 febrer 2022].
- ↑ «1.1-Definición y Clasificación de la Estadística». [Consulta: 18 febrer 2022].
- ↑ «Significado de Estadística» (en castellà). [Consulta: 18 febrer 2022].
- ↑ http://www.gencat.cat/economia/doc/doc_25560979_1.pdf Josep Antoni Vandellós i l'estadística] Àlex Costa i Xavier López, Institut d'Estadística de Catalunya
Vegeu també[modifica]
- Dada no disponible
- Distància de Mahalanobis
- Distribució gamma
- Horitzó de predicció
- Índex de Jaccard
- Institut d'Estadística de Catalunya
- Karl Pearson
- OpenMx
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Estadística |
- "NIST/SEMATECH e-Handbook of Statistical Methods", de U.S. National Institute of Standards and Technology i SEMATECH (anglès)
- "Online Statistics: An Interactive Multimedia Course of Study", de David Lane, Joan Lu, Camille Peres, Emily Zitek, et al. (en anglès)
- Rice Virtual Lab in Statistics (Rice University) (en anglès)
- Statistical Science Web (Universitat de Melbourne) (en anglès)








