Geometria riemanniana

En geometria diferencial, la geometria riemanniana és l'estudi de les varietats diferencials amb mètrica de Riemann, és a dir, d'una aplicació que a cada punt de la varietat li assigna una forma quadràtica definida positiva al seu espai tangent, una aplicació que varia lleugerament d'un punt a un altre. Això dona lloc a idees locals de (entre altres magnituds) angle, longitud de corba i de volum. A partir d'aquestes magnituds, es poden obtenir altres magnituds per integració de les magnituds locals.
Això va ser proposat de forma general per primera vegada per Bernhard Riemann durant el segle xix. Com a casos especials particulars apareixen els dos tipus convencionals (geometria el·líptica i geometria hiperbòlica) de geometria no euclidiana i també la geometria euclidiana. Totes aquestes geometries són tractades sobre la mateixa base, de la mateixa manera que una àmplia gamma de geometries amb propietats mètriques que varien de punt a punt.
Qualsevol varietat diferenciable admet una mètrica de Riemann i aquesta estructura addicional sovint ajuda a solucionar problemes de topologia diferencial. També serveix com a nivell d'entrada per a l'estructura més complicada de les varietats pseudoriemannianes, les quals (en el cas particular de tenir dimensió 4) són objectes principals de la teoria de la relativitat.
Introducció
[modifica]
La geometria riemanniana va ser plantejada per primer cop en general per Bernhard Riemann en el segle XIX. S'ocupa d'una àmplia gamma de geometries les propietats mètriques de les quals varien d'un punt a un altre, i inclou els tipus estàndard de geometria no euclidiana.
Tota varietat suau admet una mètrica de Riemann, que sovint ajuda a resoldre problemes de topologia diferencial. També serveix com a nivell d'entrada per a l'estructura més complicada de les varietats pseudoriemannianes, que (en quatre dimensions) són els principals objectes de la teoria de la relativitat general. Altres generalitzacions de la geometria riemanniana són la geometria de Finsler.
Existeix una estreta analogia de la geometria diferencial amb l'estructura matemàtica dels defectes en els cristalls regulars. Les dislocacions produeixen torsions i curvatures.[1][2]
No hi ha una introducció fàcil a la geometria riemanniana, ara bé, els següents articles poden fer-ne la funció:
Història
[modifica]Aparició de la geometria de Riemann
[modifica]Durant molts segles, el marc natural de la geometria va ser la geometria euclidiana del pla o de l'espai. Els intents infructuosos de demostrar el postulat de les paral·leles van ajudar als geòmetres a imaginar formes d'anar més enllà d'aquest marc. Així, Nikolai Lobatxevski l'any 1829 i János Bolyai l'any 1832 van introduir els primers exemples de geometria no euclidiana. Els espais amb geometria hiperbòlica que van construir es consideren ara casos especials de varietat riemannianes amb "curvatura negativa".
Uns anys abans, Gauss va estudiar la geometria diferencial de superfícies de l'espai euclidià. Per descriure-les, va introduir una magnitud fonamental, la curvatura de Gauss. Es va adonar que aquesta curvatura es podia calcular sense involuccrar l'espai circumdant, directament a partir de la informació disponible en la superfície, un teorema que va descriure com a "notable" (theorema egregium).[3] El propi Gauss va estar a punt de descobrir la geometria hiperbòlica.
El primer pas de la geometria riemanniana pròpiament dita es remunta a l'obra de Bernhard Riemann en el segle XIX i, en particular, en una conferència inaugural titulada Über die Hypothesen, welche der Geometrie zu Grunde liegen [4] (és a dir: Sobre les hipòtesis subjacents a la geometria). Es tracta d'una generalització directa de la geometria diferencial de les superfícies gaussianes en n dimensions. Aquest nou enfocament va ampliar enormement la idea de geometria no euclidiana, tot i que el seu marc conceptual va trigar diverses dècades a desenvolupar-se.
Cap a una formalització completa
[modifica]La segona meitat del segle XIX va veure principalment refinada la comprensió de la geometria hiperbòlica, a través de la introducció i l'anàlisi de diferents models de representació, que van trobar una aplicació en la relativitat especial. Van aparèixer diferents eines, que a poc a poc van desmostrar la seva gran importància. Així, la teoria de grups i àlgebres de Lie va aparèixer a la dècada de 1870, alhora que Felix Klein va subratllar la importància del concepte de grup en geometria en el seu Programa d'Erlangen. Ulisse Dini va demostrar el seu teorema de la funció implícita, que seria el preludi indispensable per a la formalització de la varietat. Henri Poincaré va desenvolupar el camp de la topologia i va introduir el grup fonamental.
Es va fer un pas decisiu quan Gregorio Ricci-Curbastro i Tullio Levi-Civita van desenvolupar el càlcul tensor en la seva obra Methods of absolute differential calculus and their applications publicada l'any 1900.[5] Tot i que el marc "espacial" encara no estava del tot clar, els càlculs avançaven molt amb els tensors. S'en va trobar una aplicació molt profunda quan Einstein, introduït a les noves geometries i a aquest càlcul tensor pel seu amic Marcel Grossmann, els va posar en ús en la seva teoria de la relativitat general l'any 1916.
Des de 1902 fins a mitjans de la dècada de 1930, es van realitzar nombrosos intents de formalitzar la noció de varietat diferenciable. Aquesta recerca va acabar amb la publicació del teorema de l'embedding de Whitney l'any 1936. La geometria riemanniana disposava per fi d'un marc clar.
Un camp de recerca en expansió
[modifica]

La classificació d'espais simètrics d'Élie Cartan l'any 1926 és un dels primers resultats importants de la geometria de Riamann. En la dècada de 1930 es van publicar els primers teoremes sobre varietats de curvatura positiva (teorema de Myers, teorema de Synge).
El teorema de l'esfera, establert l'any 1960, va marcar una espècie d'apogeu de les concepcions clàssiques basades en teoremes de comparació. Va començar llavors un renaixement de la geometria riemanniana. Va estar marcat pel desenvolupament dels mètodes de la geometria espectral, esperonat per la famosa fórmula de Mark Kac: Sentir la forma d'un tambor, i es van posar de manifest els seus vincles amb la recerca de geodèsiques periòdiques. En la dècada de 1980, Mikhaïl Grómov va introduir la noció de distància entre varietats riemannianes i va demostrar alguns resultats de convergència fructífers. Alhora, Richard Hamilton va començar a desenvolupar l'estudi del "flux de Ricci", llançant un programa de demostració de resultats topològics per geometria riemanniana mitjançant mètodes de deformació de mètriques. Aquest programa ha tingut molt d'èxit, amb la demostració de la famosa conjectura de Poincaré per Perelman l'any 2003 i una potent generalització del teorema de l'esfera (el "teorema diferencial de l'esfera") l'any 2007.
Nocions fonamentals de la geometria riemanniana, com la curvatura, troben progressivament un marc d'utilització molt més ampli que el de les varietats riemannianes pròpiament dites, i s'estenen en formes més o menys complexes als espais mètrics. Grómov va definir així els espais CAT(k) de Cartan-Aleksàndrov-Toponògov o inclús nocions de teoria geomètrica de grups, com el grup hiperbòlic. Villani, John Lott i Sturm van introduir en els anys 2010 una visió ampliada i "sintètica" de la noció de curvatura de Ricci minoritzada a partir d'una formulació del transport òptim sobre un espai mètric.
Conceptes bàsics
[modifica]Geodèsiques
[modifica]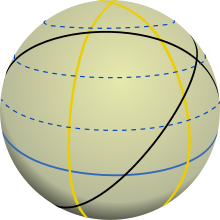
.

Les geodèsiques permeten respondre a la recerca dels camins més curts entre dos punts, igual que les línies rectes en l'espai euclidià. En realitat, les seves propietats són més complexes que les de les rectes i cal distingir entre el que es pot dir des d'un punt de vista local i el que es pot dir des d'un punt de vista més global.
Es defineixen les geodèsiques de forma general recorrent al càlcul de variacions.[6] Es considerin dos puntsx i y i el funcional de longituds en totes les corbes que uneixen x amb y amb velocitat uniforme. Les corbes que representen els punts crítics d'aquest funcional s'anomenen geodèsiques. De forma equivalent, es poden caracteritzar aquestes geodèsiques mitjançant una equació geodèsica en què intervenen el vector velocitat , el tensor mètric g i les seves derivades. També es poden introduir aquestes geodèsiques com els punts crítics d'energia i imaginar-les com bandes elàstiques estirades sobre la varietat.
Com a exemple, les geodèsiques de l'esfera són el cercle màxim. Això demostra que les geodèsiques no sempre proporcionen la distància mínima entre dos punts: per anar d'un punt a un altre de l'esfera, es pot seguir l'arc del cercle màxim més curt o el més llarg, o inclús recórrer-los diverses vegades. Tampoc existeix unicitat del camí més curt en el cas de dos punts diametralment oposats.
No obstant això, a nivell local, la situació és molt més senzilla. Es pot dir en general que les geodèsiques són "localment minimitzadores": entre dos dels seus punts, presos suficientment a prop l'un de l'altre, obtindran un mínim per a la longitud. Partint d'un punt donat, existeix una única geodèsica amb un vector tangent donat. En efecte, es pot introduir un mapa adequat centrat en . Està definit per l'aplicació exponencial en que consisteix a seguir cada una de les geodèsiques amb origen a durant un temps unitari.[7] Correspon a coordenades locals adaptades, anomenades coordenades normals.
Per formular resultats globals, només es considera el cas d'una varietat connectiva i completa. En aquest cas, les geodèsiques poden estendre per a qualsevol temps, però amb comportaments globals variables (periodicitat o no, per exemple). A més, entre dos punts donats sempre hi ha almenys una geodèsica que realitza el mínim de la longitud: tot això constitueix el teorema de Hopf–Rinow.
Curvatura
[modifica]
En la geometria de Riemann, tot i que les geodèsiques generalitzen les rectes de la geometria euclidiana, ja no s'obtenen els mateixos resultats quan al càlcul de longituds, angles i superfícies dels objectes més senzills (triangles geodèsics, cercles o esferes...). Per exemple, el fet que la suma dels angles d'un triangle és de 180° en geometria euclidiana. La curvatura pot quantificar aquestes diferències.
En el cas de superfícies en l'espai euclidià , la curvatura es denomina curvatura de Gauss. Es medeix en cada punt com un escalar. En un punt de curvatura positiva, la geometria de la superfície se sembla localment a la d'un el·lipsoide de , i en un punt de curvatura negativa a la d'un hiperboloide. Un important resultat de Gauss, el seu teorema egregi, afirma que la curvatura pot ser determinada enterament a partir de la mètrica de la superfície, és a dir, no depèn de l'embedding de la superfície en l'espai tridimensional.
Més en general, es pot, per a qualsevol varietat riemanniana, construir un objecte complex anomenat tensor de curvatura de Riemann. En coordenades locals, l'expressió d'aquest tensor implica les components de g, i les seves primeres i segones derivades. El tensor de curvatura és un objecte bastant complex d'entendre. Per contracció tensorial amb el tensor mètric es construeixen objectes més simples, el tensor de curvatura de Ricci i l'escalar de curvatura de Ricci, que contenen una part important de la informació.
Una forma de representar la noció de curvatura és donar la curvatura seccional al llarg dels diferents 2-plans de l'espai tangent a la varietat. Es tracta de la curvatura gaussiana de la superfície formada per les geodèsiques d'aquests dos plans. Aquesta forma de presentar la informació és equivalent a donar el tensor de curvatura. La idea general és que una curvatura seccional positiva indica una tendència de les geodèsiques a apropar-se entre sí, mentre que una curvatura negativa dona una tendència a allunyar-se entre sí.
Operadors de derivació
[modifica]
Dues nocions tècniques estretament relacionades amb la curvatura i la recerca de geodèsiques són connexió afí i transport paral·lel al llarg d'una corba. Es tracta de procediments que permeten connectar vectors que pertanyen a espais tangents en punts diferents de la varietat i, en conseqüència derivar camps vectorials. En una varietat diferencial general, no hi ha cap manera privilegiada de fer això. Per exemple, no és possible donar sentit al vector acceleració d'una corba traçada en la varietat.
La més que notable propietat de les varietats riemannianes, que Marcel Berger no va dubtar a qualificar de "miracle", és que existeix una connexió naturalment associada a la mètrica, la connexió de Levi-Civita. En efecte, es demostra que existeix una connexió única que preserva l'estructura euclidiana quan connecte els diferents espais tangens i que dona segones derivades simètriques: aquesta afirmació que té un paper fundacional s'anomena teorema fonamental de la geometria de Riemann. Utilitzant la connexió de Levi-Civita, és possible transportar un vector tangent al llarg d'una corba donada.[8]
La figura a l'esquerra mostra un exemple de tal transport. Però, més en general, es pot fer càlcul diferencial de qualsevol ordre sobre qualsevol tipus de tensors.
Es defineix el tensor de curvatura de Riemann a partir de la connexió de Levi-Civita, que alhora es deriva de la mètrica g. En aquesta presentació, la curvatura pot interpretar-se com la mesura infinitesimal de l'error de retorn en l'origen per a un vector que es transporta al llarg d'una corba tancada. Algunes introduccions a la geometria riemanniana també introdueixen geodèsiques a partir de la noció de connexió.[9]
També és possible construir una generalització del laplacià per a l'entorn riemannià: es tracta de l'operador Laplace-Beltrami. Es pot aplicar a funcions, o més en general, a formes diferencials, utilitzant la dualitat de Hodge.[10]
Teoremes clàssics de la geometria riemanniana
[modifica]Ara ve una llista no completa dels teoremes més clàssics de la geometria riemanniana. L'elecció s'ha fet depenent de la seva importància i la seva simplicitat de la formulació.
Teoremes generals
[modifica]- Teorema de Gauss-Bonnet La integral de la curvatura de Gauss en una varietat riemanniana compacta de 2 dimensions és igual a , aquí denota la característica d'Euler de M.
- Teorema d'immersió de Nash també anomenat Teorema Fonamental de la geometria riemanniana. Indica que cada varietat de Riemann pot estar isomètricament submergida en un espai euclidià Rn.
Referències
[modifica]- ↑ Kleinert, Hagen. Campos gauge en la materia condensada Vol II, 1989, p. 743-1440.
- ↑ Kleinert, Hagen. Campos multivaluados en materia condensada, electromagnetismo y gravitación, 2008, p. 1-496.
- ↑ Morgan, Frank. Riemannian geometry: a beginner's guide. Wellesley, MA: A.K. Peters, 1998. ISBN 978-1-56881-073-7.
- ↑ «Ueber die Hypothesen, welche der Geometrie zu Grunde liegen.» (en alemany). [Consulta: 24 juny 2024].
- ↑ O'Connor, J. J.; Robertson, E. F. «Levi-Civita biography» (en anglès). McTutor. Universitat de St Andrews. Arxivat de l'original el 2006-06-20. [Consulta: 24 juny 2024].
- ↑ Jost, 2008, p. 17, Definició 1.4.2.
- ↑ Gallot, Hulin i Lafontaine, 2004, p. 81, Definició 2.86.
- ↑ Berger, Marcel. A Panoramic View of Riemannian Geometry (en anglès). Springer Science & Business Media, 2012-12-06, p. 697-698, 705. ISBN 978-3-642-18245-7.
- ↑ Gallot, Hulin i Lafontaine, 2004, p. 77, Definició 2.77.
- ↑ Jost, 2008, p. 83, Definició 2.1.2.
Bibliografia
[modifica]- Gallot, Sylvestre; Hulin, Dominique; Lafontaine, Jacques. Riemannian Geometry (en anglès). Springer Science & Business Media, 2004. ISBN 978-3-540-20493-0.
- Jost, Jürgen. Riemannian Geometry and Geometric Analysis (en anglès). Springer Science & Business Media, 2008. ISBN 978-3-540-77341-2.





