Corba de Lissajous


En matemàtiques, una corba de Lissajous o corba de Bowditch és la que té per equacions paramètriques
que descriu un moviment harmònic simple. Aquesta família de corbes va ser investigada per Nathaniel Bowditch el 1815, i més tard i en més detall per Jules Antoine Lissajous en 1857.
L'aspecte de la figura és altament sensible al quocient a/b. Per un quocient d'1, la figura és una el·lipse, amb casos especials que inclouen circumferències (A = B, δ = π/2 radians) i rectes (δ = 0). Una altra corba de Lissajous senzilla és la paràbola (a/b = 2, δ = π/2). Altres quocients donen corbes més complicades, les quals només són tancades si a/b és un nombre racional. L'aspecte visual d'aquestes corbes sovint suggereix un nus tridimensional, a més moltes classes de nusos, incloent-hi el nusos que es coneixen com a nusos de Lissajous, es projecten al pla com a corbes de Lissajous.
Les corbes de Lissajous quan a=1, b=N (nombre natural) i són polinomis de Txebixov de primera classe de grau N.
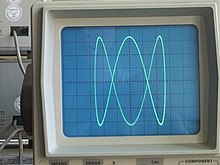
Quan s'apliquen dues entrades sinusoidals desfasades a un oscil·loscopi en mode X-Y amb la relació de fase adequada, apareix una corba de Lissajous. Les corbes de Lissajous també es poden traçar mecànicament amb un harmonògraf.
Si en un oscil·loscopi x és CH1 i y és CH2, A és l'amplitud de CH1 i B és l'amplitud de CH2, a és la freqüència de CH1 i b és la freqüència de CH2, llavors és el quocient de freqüències entre els dos canals, i finalment, δ és el desfase de CH1.
A continuació hi ha alguns exemples de corbes de Lissajous amb δ = π/2, a senar, b parell, |a − b| = 1.
-
a = 1, b = 2 (1:2)
-
a = 3, b = 2 (3:2)
-
a = 3, b = 4 (3:4)
-
a = 5, b = 4 (5:4)
-
a = 5, b = 6 (5:6)
-
a = 9, b = 8 (9:8)
Tot i que tenen una aparença semblant, les corbes espirogràfiques són diferents, atès que aquestes estan limitades una àrea circular mentre que les corbes de Lissajous estan limitades per un rectangle (±A, ±B).
Vegeu també[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Corba de Lissajous |









