Sistema de coordenades

En geometria, un sistema de coordenades és un sistema que utilitza un o més números o coordenades, per determinar de forma única la posició d'un punt o d'un altre element geomètric.[1][2] És un conjunt de valors que permeten definir unívocament la posició de qualsevol punt en l'espai respecte a un punt de referència. L'ús d'un sistema de coordenades permet que determinats problemes en geometria es tradueixin en problemes numèrics, i a l'inrevés, aquesta és la base de la geometria analítica.[3]
El conjunt d'eixos, punts o plans, que conflueixen en l'origen i a partir dels quals es calculen les coordenades s'anomena sistema de referència.
Història[modifica]
Els primers sistemes de coordenades com a tal els trobem a mitjans del segle xvi. Rafael Bombelli (20 de gener de 1526 (bateig)-1572;[4] matemàtic italià) va utilitzar la recta numèrica per a representar els diferents nombres com a longituds en aquesta recta; d'aquí en va extreure la idea dels nombres reals, i del primer sistema de coordenades en la recta.[5]
Posteriorment, René Descartes (1596-1650), filòsof i matemàtic francès, va introduir el nou concepte de coordenades en el pla, i al relacionar els punts del pla i les paral·lels de nombres reals, va obtenir els que actualment s'anomenen sistemes de coordenades cartesianes.[5]
Hi ha diverses relacions de la introducció de les coordenades polars com a part d'un sistema formal de coordenades. La història completa de la qüestió es descriu a Origin of Polar Coordinates.[6] Grégoire de Saint-Vincent i Bonaventura Cavalieri varen introduir independentment els conceptes a mitjans del segle disset. Saint-Vincent ho va escriure en privat el 1625 i va publicar el seu treball el 1647, mentre que Cavalieri va publicar el seu el 1635 amb una versió corregida que va aparèixer el 1653. Cavalieri va ser el primer a fer servir les coordenades polars per resoldre un problema referent a l'àrea dins d'una espiral d'Arquimedes. Més tard, Blaise Pascal va fer servir les coordenades polars per calcular la longitud de l'arc de la paràbola.
En l'obra Mètode de les fluxions (escrit el 1671, publicat el 1736), Isaac Newton examina les transformacions entre coordenades polars (de les quals ell en diu la "Setena Manera Per les Espirals"), i uns altres nou sistemes de coordenades.[7] També se li atribueix el primer ús de coordenades negatives en una col·lecció de figures i gràfiques dels polinomis de tercer grau en el seu llibre Enumeratio linearum tertii ordinis, o Enumeració de les corbes de tercer grau. En la revista Acta Eruditorum (1691), Jacob Bernoulli feia servir un sistema amb un punt sobre una línia, anomenats pol i eix polar respectivament. Les coordenades s'especificaven per la distància al pol i l'angle respecte a l'eix polar. El treball d'en Bernoulli s'estén a trobar el radi de curvatura de corbes expressades en aquest sistema de coordenades.
El terme actual coordenades polars s'ha atribuït a Gregorio Fontana (Villa di Nogaredo, 7 de desembre de 1735 - Milà, 24 d'agost de 1803; matemàtic italià) i el feien servir els escriptors italians del segle 18.[8][9] Alexis Clairaut va ser el primer a pensar en coordenades polars en tres dimensions, i Leonhard Euler va ser el primer a desenvolupar-les.[6]
El 1827, en l'obra Der barycentrische Calcül, August Ferdinand Möbius va introduir el concepte de coordenades homogènies' o coordenades projectives[10][11]
El sistema de coordenades UTM va ser desenvolupat pel Cos d'Enginyers de l'Exèrcit dels Estats Units a la dècada de 1940. El sistema es va basar en un model el·lipsoïdal de la Terra. Es va usar l'el·lipsoide de Clarke de 1866 per al territori dels 48 estats contigus. Per a la resta del món-inclosos Alaska i Hawaii - es va fer servir l'el·lipsoide Internacional. Actualment es fa servir l'el·lipsoide WGS84 com a model de base per al sistema de coordenades UTM.
Sistemes de coordenades utilitzats[modifica]
Recta numèrica[modifica]
L'exemple més simple d'un sistema de coordenades és la identificació de punts en una recta amb nombres reals utilitzant la recta numèrica. En aquest sistema, s'escull un punt arbitrari O (l'origen) en una línia. La coordenada d'un punt P es defineix com la distància signada d'O a P, on la distància signada és la distància és positiva o negativa segons en quina banda de la línia es troba P. A cada punt se li dona una coordenada única i cada nombre és la coordenada d'un punt únic.[12][1]

Sistema de coordenades cartesianes[modifica]

 El sistema de coordenades cartesianes o sistema cartesià és un sistema de coordenades que referencia respecte ja sigui un sol eix (línia recta), respecte a dos eixos (un pla) o respecte a tres eixos (en l'espai) perpendiculars entre si (pla i espai), que es tallen en un punt anomenat origen de coordenades (anàlogament, a , es poden definir sistemes n-dimensionals). En el pla, les coordenades cartesianes (o rectangulars) "x" i "y", que s'anomenen respectivament abscissa i ordenada. Per convenció, l'origen del sistema de coordenades cartesianes és el punt (0,0,0). Les coordenades cartesianes es defineixen per dos eixos (X,Y) quan es tracta de fixar punts en el pla i per tres (X,Y,Z) quan es vol fer això en l'espai. Es consideren eixos mútuament perpendiculars que es tallen en l'origen. Les coordenades d'un punt qualsevol vindran donades per les projeccions de la distància entre el punt i l'origen sobre cadascun dels eixos.
El sistema de coordenades cartesianes o sistema cartesià és un sistema de coordenades que referencia respecte ja sigui un sol eix (línia recta), respecte a dos eixos (un pla) o respecte a tres eixos (en l'espai) perpendiculars entre si (pla i espai), que es tallen en un punt anomenat origen de coordenades (anàlogament, a , es poden definir sistemes n-dimensionals). En el pla, les coordenades cartesianes (o rectangulars) "x" i "y", que s'anomenen respectivament abscissa i ordenada. Per convenció, l'origen del sistema de coordenades cartesianes és el punt (0,0,0). Les coordenades cartesianes es defineixen per dos eixos (X,Y) quan es tracta de fixar punts en el pla i per tres (X,Y,Z) quan es vol fer això en l'espai. Es consideren eixos mútuament perpendiculars que es tallen en l'origen. Les coordenades d'un punt qualsevol vindran donades per les projeccions de la distància entre el punt i l'origen sobre cadascun dels eixos.
El valor de cada una de les coordenades d'un punt qualsevol (per exemple, A) és igual a la projecció ortogonal del vector de posició de l'anomenat punt () sobre un eix determinat:
Cada un dels eixos està definit per un vector director i per l'origen de coordenades. Per exemple, l'eix x està definit per l'origen de coordenades (O) i un vector () tal que:
- , que el seu mòdul és .
El valor de la coordenada x d'un punt és igual a la projecció ortogonal del vector de posició de l'anomenat punt sobre l'eix x.
S'anomenen coordenades cartesianes en honor de René Descartes (1596-1650), el cèlebre filòsof i matemàtic francès que va voler fonamentar el seu pensament filosòfic amb la necessitat de prendre un «punt de partida» sobre el qual edificar tot el coneixement. Com a creador de la geometria analítica, Descartes també va començar prenent un «punt de partida», el sistema de referència cartesià, per poder representar la geometria plana, que fa servir només dues rectes perpendiculars entre si que es tallen en un punt anomenat «origen de coordenades».
Sistema de coordenades polars[modifica]

Les coordenades polars es defineixen per un eix que passa per l'origen, anomenat eix polar. La primera coordenada és la distància entre l'origen i el punt considerat, mentre que la segona és l'angle que formen l'eix polar i la recta que passa per tots dos punts. El sistema de coordenades polars és un sistema de coordenades de dues dimensions en el que cada punt en un pla està determinat per un angle i una distància. El sistema de coordenades polars és especialment útil quan la relació entre dos punts s'expressa més bé en termes d'angles i distàncies. En el sistema més conegut, el cartesià o de coordenades rectangulars, aquestes relacions cal trobar-les a partir de les funcions trigonomètriques.
Com que el sistema de coordenades és de dues dimensions, cada punt ve determinat per dues coordenades polars: la coordenada radial i la coordenada angular. La coordenada radial (normalment denotada per r) denota la distància del punt al punt central (conegut com a pol i equivalent a l'origen en el sistema cartesià). La coordenada angular (també anomenada angle polar o angle azimutal, i normalment denotat per θ o t) denota l'angle positiu (o angle mesurat en sentit antihorari) per arribar al punt a partir de l'eix polar o radi de 0° (que és equivalent a l'eix x positiu en les coordenades cartesianes).[13]
Si bé hi ha exemples que els conceptes d'angle i ràdio es coneixen i manegen des de l'antiguitat, no és sinó fins al segle xvii, posterior a la invenció de la geometria analítica, en què es pot parlar del concepte formal de sistema coordenades polars. No obstant això, el concepte abstracte de sistema de coordenada polar es deu a Isaac Newton, qui en el seu Mètode de les fluxions escrit el 1671 i publicat el 1736, introdueix vuit nous sistemes de coordenades (a més de les cartesianes) per resoldre problemes relatius a tangents i corbes, un dels quals, el setè, és el de les coordenades polars.[14] El 1691, en la revista Acta Eruditorum, Jacob Bernoulli va utilitzar un sistema amb un punt en una línia, anomenant-los pol i eix polar respectivament. Les coordenades s'especificaven per la distància al pol i l'angle respecte a l'eix polar. El treball de Bernoulli va servir de base per a trobar el radi de curvatura de corbes expressades en aquest sistema de coordenades.
El terme actual de coordenades polars s'atribueix a Gregorio Fontana, i va ser utilitzat pels escriptors italians del segle xviii. El terme apareix per primera vegada en anglès en la traducció de 1816 feta per George Peacock del Traité du calcul différentiel et du calcul intégral (Tractat del càlcul diferencial i del càlcul integral) de Sylvestre François Lacroix,[9] mentre que Alexis Clairault ser el primer que va pensar a ampliar les coordenades polars a tres dimensions.
Sistema de coordenades cilíndriques[modifica]
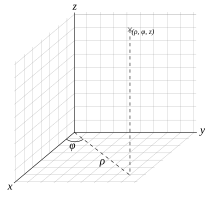
El sistema de coordenades cilíndriques és una generalització del sistema de coordenades polars pla, al que s'afegeix un tercer eix de referència perpendicular als altres dos. Aquest sistema és especialment útil en problemes de simetria axial.
La notació usada per aquest sistema de coordenades no és uniforme. L'estàndard ISO 31-11 l'estableix com . Però, en molts casos l'azimut es denota com . La coordenada radial de vegades s'anomena mentre que a coordenada vertical de vegades és referida com .
En el sistema de coordenades cilíndriques, a cada punt P de l'espai se li assignen les coordenades de forma que:
- és la distància de l'origen O a P', la projecció ortogonal del punt P al pla XY. O cosa que és el mateix: la distància de P a l'eix z.
- és l'angle entre el semieix positiu x i la recta OP', mesurat en sentit contrari a les agulles del rellotge.
- el mateix que en el sistema de coordenades cartesià és a dir, la distància del punt P al pla xy.
Sistema de coordenades esfèriques[modifica]

El sistema de coordenades esfèriques està format per tres eixos mútuament perpendiculars que es tallen en l'origen. La primera coordenada és la distància entre l'origen i el punt, essent les altres dues els angles que cal girar per arribar a la posició del punt. Quan s'estén el concepte de coordenades esfèriques a espais de dimensió superior llavors s'anomena com a coordenades hiperesfèriques.
Hi ha diverses convencions per a representar les tres coordenades. D'acord amb l'Organització Internacional per a l'Estandardització (ISO 31-11), la notació és (r, θ, φ) per indicar la distància radial, l'angle zenital i l'angle azimutal respectivament.
Les tres coordenades (r, θ, φ) es defineixen com:
- r ≥ 0 és la distància de l'origen al punt P.
- 0 ≤ θ ≤ π és l'angle entre la part positiva de l'eix z i la recta que passa per l'origen i P.
- 0 ≤ φ < 2π és l'angle entre la part positiva de l'eix x-axis i la recta que passa per l'origen i P projectada sobre el pla xy.
φ s'anomena l'azimut, mentre que θ s'anomena el zenit, la colatitud o l'angle polar.
θ i φ deixen de tenir sentit quan r = 0 i φ deixa de tenir sentit quan sin(θ) = 0 (a θ = 0 i a θ = π).
Sistema de coordenades homogènies[modifica]

El sistema de coordenades homogènies assigna a cada punt una tupla de n+1 components denotada sovint [x0 : x1 : ... : xn ] que estan definides excepte multiplicació per escalars [λx0 : λx1 : ... : λxn ] λ≠0, és a dir, que dues n+1-ples representen el mateix punt en tant que es conservi la proporció entre les seves components. Aquest tipus de coordenades són molt usades en geometria projectiva, on representen els vectors de l'espai vectorial usat per a definir cada espai projectiu. També es fan servir, per exemple, al denotar les rectes del pla com a equacions en forma general Ax+By+C=0. Vegeu també coordenades homogènies i Geometria projectiva#Coordenades homogènies.
Coordenades geogràfiques[modifica]
 PDF, 3.4MB)
PDF, 3.4MB)Les coordenades geogràfiques corresponen al concepte de la latitud i la longitud, és a dir, que són els paràmetres que determinen la posició d'un punt de la superfície terrestre. Les línies de referència són l'equador terrestre i un meridià inicial (el de Greenwich per conveni). La longitud d'un punt P de la superfície terrestre és l'arc d'equador comprès entre el punt d'intersecció del meridià inicial de Greenwich amb l'equador i el punt d'intersecció del meridià local de P amb l'equador.
La latitud de P és l'arc del meridià local de P comprès entre l'equador i P, mesurat de 0° a 90° a cada hemisferi a partir de l'equador.
La forma real de la Terra fa que l'extensió d'un grau de longitud o de latitud sigui diferent en diferents punts geogràfics per la qual cosa per a més exactitud s'han fet correccions del càlcul de la latitud. La posició geogràfica d'un punt queda completament establerta en especificar l'altitud.
La latitud i la longitud poden mostrar-se en tres formats equivalents (sigles en anglès):
- Graus.Decimals Decimal Degree (DD) exemple 41.333- 106..500
- Graus:Minuts Degree Minute (DM) exemple 41:20- 106:30
- Graus:Minuts:Segons Degree Minute Second (DMS) exemple 41:20:00- 106:30:00
Coordenades astronòmiques o celestes[modifica]
Les coordenades astronòmiques o coordenades celestes són qualsevol sistema de coordenades que s'utilitza per a determinar la posició d'un cos sobre l'esfera celeste. Segons els punts de referència que s'escullin es poden utilitzar diferents sistemes de coordenades. La raó per la qual hi ha diferents referències per determinar un mateix punt és que les coordenades geocèntriques serveixen per distingir qualsevol punt respecte on ens trobem, però els càlculs sobre les òrbites dels cossos celestes es fan molt complicades. Es fa més senzill (que no fàcil) si es pren la referència del punt segons el que orbita el cos a estudiar.
Es tracta de determinar les posicions aparents que ocupen els astres al firmament, sobre l'anomenada esfera celeste. Així calen dos paràmetres angulars per a situar sobre aquesta esfera qualsevol astre, el valor numèric dels quals paràmetres és distint segons el sistema de coordenades elegit que són anomenats entre altres: celestial, horitzontal, equatorial, eclíptic, galàctic, extragalàctic, supergalàctic i binari.
Coordenades equatorials[modifica]
Les coordenades equatorials són un sistema de coordenades celestes que permeten determinar la posició d'un cos respecte a l'equador celeste i el primer punt d'Àries. Les seves dues coordenades són l'ascensió recta i la declinació.
Coordenades eclíptiques[modifica]
Les coordenades eclíptiques són un sistema de coordenades celestes que permet determinar la posició d'un cos respecte al pla de l'eclíptica i al primer punt Àries. Les dues coordenades són la longitud celeste i la latitud celeste
Coordenades curvilínies[modifica]
Coordenades curvilínies generals[modifica]
Un sistema de coordenades curvilínies és la forma més general de parametritzar o etiquetar els punts d'un espai localment euclidià o varietat diferenciable (globalment l'espai pot ser euclidià però no necessàriament). Si tenim un espai localment euclidià M de dimensió m, podem construir un sistema de coordenades curvilini local entorn d'un punt p sempre a partir de qualsevol homeomorfisme que compleixi:
Per a qualsevol punt q pròxim a p es defineixen les seves coordenades curvilínies:
Si l'espai localment euclidià té l'estructura de varietat de Riemann es poden classificar a certs sistemes de coordenades curvilínies en sistemes de coordenades ortogonals i quan és un sistema de coordenades ortonormals. Les coordenades cilíndriques i les esfèriques són casos particulars de sistemes de coordenades ortogonals sobre l'espai euclidià .
Coordenades curvilínies ortogonals[modifica]
Un sistema de coordenades curvilínies se les anomena ortogonals qual el tensor mètric expressat en aquestes coordenades té una forma diagonal. Quan això succeeix, moltes de les fórmules del càlcul vectorial diferencial es poden escriure de forma particularment senzilla en aquestes coordenades, podent-se aprofitar aquest fet quan existeix per exemple, simetria axial, esfèrica o d'un altre tipus fàcilment representable en aquestes coordenades curvilínies ortogonals.
Les coordenades esfèriques i cilíndriques són casos particulars de coordenades curvilínies ortogonals.
Sistema de Coordenades Universal Transversal de Mercator[modifica]

El Sistema de Coordenades Universal Transversal de Mercator (en anglès Universal Transverse Mercator, UTM) és un sistema de coordenades basat en la projecció cartogràfica transversa de Mercator, que es construeix com la projecció de Mercator normal, però en comptes de fer-la tangent a l'Equador, es fa tangent a un meridià. A diferència del sistema de coordenades geogràfiques, expressades en longitud i latitud, les magnituds en el sistema UTM s'expressen en metres únicament al nivell del mar que és la base de la projecció de l'el·lipsoide de referència.[15]
La "projecció transversa de Mercator" és una variant de la "projecció de Mercator" que va ser desenvolupada pel geògraf flamenc Gerardus Mercator a 1659. Aquesta projecció és "conforme", és a dir, que conserva els angle si gairebé no distorsiona les formes però inevitablement sí que ho fa amb distàncies i àrees. El sistema UTM implica l'ús d'escales no lineals és per a les coordenades X i Y (longitud i latitud cartogràfiques) per assegurar que el mapa projectat resulti conforme.
Canvis de coordenades[modifica]
En la resolució de problemes físics i matemàtics és comuna l'estratègia del canvi de coordenades. En essència un canvi de coordenades suposa canviar les variables de què depèn el problema, a altres coordenades diferents en les que el problema pot tenir una forma equivalent però més simple, que permet trobar la solució amb més facilitat.
Més formalment un canvi de coordenades pot representar-se per un homeomorfisme o aplicació bijectiva i diferenciable (amb inversa també diferenciable) entre dos conjunts de , aquí anomenats i :
Aquest canvi de variable permet, per exemple, reescriure integrals de la següent forma:
On:
- representa la funció que pretén integrar-se expressada en les velles i les noves coordenades.
- és el jacobià del canvi de coordenades.
- és el domini d'integració expressat en les velles i les noves coordenades.
Per transformar o reescriure equacions diferencials en termes de les noves coordenades s'usen les lleis de transformació tensorial:
Origen de coordenades[modifica]

L'origen de coordenades és el punt de referència d'un sistema de coordenades. En aquest punt, el valor de totes les coordenades del sistema és nul. No obstant això, en alguns sistemes de coordenades no és necessari establir nul·les totes les coordenades. Per exemple, en un sistema de coordenades esfèriques és suficient amb establir el radi nul (), sent indiferents els valors de latitud i longitud.
En un sistema de coordenades cartesianes, l'origen és el punt en què els eixos del sistema es tallen.
Mapes de coordenades[modifica]
El concepte d'un mapa de coordenades o taula és central en la teoria de les varietats. Un mapa de coordenades és essencialment un sistema de coordenades per a un subconjunt d'un espai donat amb la propietat que cada punt té exactament un conjunt de coordenades. Més precisament, un mapa de coordenades és un homeomorfisme d'un obert d'un espai X per a un subconjunt obert de . Sovint no és possible proporcionar un sistema de coordenades consistent per tot un espai. En aquest cas, una col·lecció de mapes de coordenades es posen junts per formar un atles cobrint l'espai. Un espai equipat amb un atles es diu un col·lector i estructura addicional pot definir-se en un col·lector de si l'estructura és coherent on els mapes de coordenades se superposen. Per exemple, un varietat diferenciable és un col·lector on el canvi de coordenades d'un mapa de coordenades a un altre és sempre una funció diferenciable.
Vegeu també[modifica]
Referències[modifica]
- ↑ 1,0 1,1 Woods, Frederick S. Higher Geometry (en anglès). Ginn and Co., 1922, p. 1.
- ↑ Weisstein, Eric W., «Coordinate System» a MathWorld (en anglès).
- ↑ Weisstein, Eric W., «Coordinates» a MathWorld (en anglès).
- ↑ «Rafael Bombelli» (en alemany). Arxivat de l'original el 2013-10-25. [Consulta: 9 maig 2013].
- ↑ 5,0 5,1 «Sistema de coordenades». Gran Enciclopèdia Catalana. Barcelona: Grup Enciclopèdia Catalana.
- ↑ 6,0 6,1 Coolidge, Julian «The Origin of Polar Coordinates» (en anglès). American Mathematical Monthly, 59, 1952, pàg. 78–85.
- ↑ Boyer, C. B. «Newton as an Originator of Polar Coordinates» (en anglès). American Mathematical Monthly, 56, 1949, pàg. 73–78.
- ↑ Miller, Jeff. «Earliest Known Uses of Some of the Words of Mathematics». Arxivat de l'original el 1999-10-03. [Consulta: 10 setembre 2006].
- ↑ 9,0 9,1 Smith, David Eugene. History of Mathematics, Vol II (en anglès). Boston: Ginn and Co., 1925, p. 324.
- ↑ O'Connor, John J.; Robertson, Edmund F. «August Ferdinand Möbius» (en anglès). MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland.
- ↑ Smith, David Eugene. History of Modern Mathematics. J. Wiley & Sons, 1906, p. 53.
- ↑ «Number Line» (en anglès). Mathwords.
- ↑ Brown, Richard G. Andrew M. Gleason. Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis (en anglès). Evanston, Illinois: McDougal Littell, 1997. ISBN 0-395-77114-5.
- ↑ Boyer, C. B. «Newton as an Originator of Polar Coordinates» (en anglès). American Mathematical Monthly, 56, 1949, pàg. 73-78. 10.2307/2306162.
- ↑ Deetz, Charles H. Elements de projecció de mapes i la seva aplicació a la construcció de mapes i cartes (en anglès). Washington: Secretaria d'Estat dels Estats Units d'Amèrica, 1944.
Bibliografia[modifica]
- Voitsekhovskii, M.I.; A.B., Ivanov. Coordinates", a Hazewinkel, Michiel: Encyclopaedia of Mathematics (en anglès). Springer, 2001. ISBN 978-1556080104.
- Geometry of Differential Forms (en anglès). AMS Bookstore, 2001, p. 12. ISBN 0821810456.
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Sistema de coordenades |
- School of Informatics. «Hexagonal Coordinate System» (en anglès). The University of Edinburgh. [Consulta: 9 maig 2013].
- «Epsilones - La invención de los sistemas de coordenadas» (en castellà). Arxivat de l'original el 19 de juliol 2013. [Consulta: 9 maig 2013].
- School of Informatics. «Hexagonal Coordinate System» (en anglès). The University of Edinburgh. [Consulta: 9 maig 2013].


























