Coordenades polars

El sistema de coordenades polars és, en matemàtiques, un sistema de coordenades de dues dimensions en el qual cada punt en un pla està determinat per un angle i una distància. El sistema de coordenades polars és especialment útil quan la relació entre dos punts s'expressa més bé en termes d'angles i distàncies. En el sistema més conegut, el cartesià o de coordenades rectangulars, aquestes relacions cal trobar-les a partir de les funcions trigonomètriques.

Com que el sistema de coordenades és de dues dimensions, cada punt ve determinat per dues coordenades polars: la coordenada radial i la coordenada angular. La coordenada radial (normalment denotada per r) denota la distància del punt al punt central (conegut com a pol i equivalent a l'origen en el sistema cartesià). La coordenada angular (també anomenada angle polar o angle azimutal, i normalment denotat per θ o t) denota l'angle positiu (o angle mesurat en sentit antihorari) per arribar al punt a partir de l'eix polar o radi de 0° (que és equivalent a l'eix x positiu en les coordenades cartesianes).^[1]

Història[modifica]

Els conceptes d'angle i de radi varen ser estudiats pels pobles antics del primer mil·lenni abans de la nostra era. L'astrònom Hiparc de Nicea va crear una taula de la funció corda que donava la longitud de la corda per a cada angle, i hi ha referències que feia servir coordenades polars per establir les posicions estel·lars.^[2] En l'obra De les espirals, Arquimedes descriu l'espiral d'Arquimedes, una funció en la qual el radi creix linealment amb l'angle. Ara bé, el treball grec no es va estendre fins a un sistema complet de coordenades.

Hi ha diverses relacions de la introducció de les coordenades polars com a part d'un sistema formal de coordenades. La història completa de la qüestió es descriu a Origin of Polar Coordinates.^[3] Grégoire de Saint-Vincent i Bonaventura Cavalieri varen introduir independentment els conceptes a mitjans del segle disset. Saint-Vincent ho va escriure en privat el 1625 i va publicar el seu treball el 1647, mentre que Cavalieri va publicar el seu el 1635 amb una versió corregida que va aparèixer el 1653. Cavalieri va ser el primer a fer servir les coordenades polars per resoldre un problema referent a l'àrea dins d'una espiral d'Arquimedes. Més tard, Blaise Pascal va fer servir les coordenades polars per calcular la longitud de l'arc de la paràbola.

En l'obra Method of Fluxions (Mètode de les fluxionsescrit el 1671, publicat el 1736), Isaac Newton examina les transformacions entre coordenades polars (de les quals ell en diu la "Setena Manera Per les Espirals", i uns altres nou sistemes de coordenades.^[4] En la revista Acta Eruditorum (1691), Jacob Bernoulli feia servir un sistema amb un punt sobre una línia, anomenats pol i eix polar respectivament. Les coordenades s'especificaven per la distància al pol i l'angle respecte a l'eix polar. El treball d'en Bernoulli s'estén a trobar el radi de curvatura de corbes expressades en aquest sistema de coordenades.

El terme actual coordenades polars s'ha atribuït a Gregorio Fontana i el feien servir els escriptors italians del segle 18.^[5]^[6] Alexis Clairaut va ser el primer a pensar en coordenades polars en tres dimensions, i Leonhard Euler va ser el primer a desenvolupar-les.^[3]

Representació dels punts en coordenades polars[modifica]

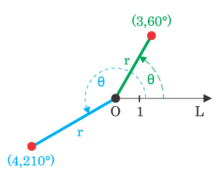
Els punts (3,60°) i (4,210°) en un sistema de coordenades polars

Cada punt en un sistema de coordenades polars es pot descriure amb les dues coordenades polars, les quals es diuen habitualment $r$ (la coordenada radial) i θ (la coordenada angular, angle polar, o angle azimutal, que de vegades es representa com φ o $t$ ). La coordenada $r$ representa la distància radial al pol, i la coordenada θ representa l'angle (mesurat en sentit contrari de les agulles del rellotge) respecte del radi d'angle 0° (anomenat de vegades l'eix polar), conegut com la part positiva de l'eix x en el sistema de coordenades cartesià.^[1]

Per exemple, les coordenades polars (3, 60°) indiquen el punt ubicat a 3 unitats de distància del pol sobre el radi que forma 60° respecte de la part positiva de l'eix x. Les coordenades (−3, 240°) també indiquen aquest mateix punt perquè una distància radial negativa s'identifica amb una distància positiva mesurada sobre el radi oposat (el radi reflectit respecte de l'origen, que es diferencia de l'original en un gir de 180°).

Un aspecte important del sistema de coordenades polar, que no es dona en el sistema de coordenades cartesianes, és que un únic punt es pot expressar amb un nombre infinit de coordenades diferents. Això és a causa del fet que es pot donar un nombre qualsevol de voltes senceres entorn del pol sense afectar la posició dels punts representats. En general, el punt ( $r$ , θ) es pot representar com ( $r$ , θ ± $n$ ×360°) o (− $r$ , θ ± (2 $n$ + 1)180°), on $n$ és qualsevol enter.^[7]

Les coordenades (0, θ) es fan servir, per convenció, per representar el pol, atès que independentment de la coordenada θ, qualsevol punt sobre un radi de longitud 0 estarà sempre al pol.^[8] Per obtenir una representació única de cada punt, és habitual de limitar $r$ als nombres no negatius $r$ ≥ 0 i θ a l'interval [0, 360°) o (−180°, 180°] (o, en radians, [0, 2π) o (−π, π]).^[9]

Els angles, quan es fa servir la notació polar, en general s'expressen tant en graus com en radians, fent servir la conversió 2π rad = 360°. La tria depèn fonamentalment del context. En navegació marítima es fan servir els graus, mentre que en algunes aplicacions en física (especialment en mecànica de rotació) i gairebé tota la literatura sobre càlcul infinitesimal fan servir els radians.^[10]

Conversió entre coordenades polars i coordenades cartesianes[modifica]

Les dues coordenades polars $r$ i θ es poden convertir en les coordenades cartesianes $x$ i $y$ emprant les funcions trigonomètriques sinus i cosinus:

x=r\cos \theta \,

y=r\sin \theta ,\,

Per transformar les dues coordenades cartesianes $x$ i $y$ en coordenades polars $r$ i $\theta$ cal fer el següent. Per a la $r$ es pot aplicar el teorema de Pitàgores:

r={\sqrt {x^{2}+y^{2}}}\,

.

Per determinar la coordenada angular θ, s'ha de tenir en compte el següent:

Per a $r$ = 0, es pot fixar θ com qualsevol nombre real.
Per a $r$ ≠ 0, s'ha de limitar el valor de θ a un valor en un interval de mida 2π perquè hi hagi una representació única per a θ. Normalment es fan servir els intervals [0, 2π) i (−π, π].

A fi d'obtenir θ en l'interval [0, 2π), es pot fer servir el següent (on $\arctan$ denota la inversa de la tangent):

\theta ={\begin{cases}\arctan({\frac {y}{x}})&{\mbox{si }}x>0{\mbox{ i }}y\geq 0\\\arctan({\frac {y}{x}})+2\pi &{\mbox{si }}x>0{\mbox{ i }}y<0\\\arctan({\frac {y}{x}})+\pi &{\mbox{si }}x<0\\{\frac {\pi }{2}}&{\mbox{si }}x=0{\mbox{ i }}y>0\\{\frac {3\pi }{2}}&{\mbox{si }}x=0{\mbox{ i }}y<0\end{cases}}

A fi d'obtenir θ en l'interval (−π, π], es pot fer servir el següent

\theta ={\begin{cases}\arctan({\frac {y}{x}})&{\mbox{si }}x>0\\\arctan({\frac {y}{x}})+\pi &{\mbox{si }}x<0{\mbox{ i }}y\geq 0\\\arctan({\frac {y}{x}})-\pi &{\mbox{si }}x<0{\mbox{ i }}y<0\\{\frac {\pi }{2}}&{\mbox{si }}x=0{\mbox{ i }}y>0\\-{\frac {\pi }{2}}&{\mbox{si }}x=0{\mbox{ i }}y<0\end{cases}}

Equacions polars[modifica]

D'una equació que defineix una corba algebraica expressada en coordenades polars, se'n diu equació polar. En molts casos, aquesta equació es pot especificar a base de definir $r$ com una funció de θ. Llavors, la corba que en resulta consisteix en punts de la forma ( $r$ (θ), θ) i pot ser considerada com la gràfica de la funció polar $r$ .

A partir de l'equació d'una funció polar $r=f(\theta )$ es poden deduir diferents formes de simetria. Si $r$ (−θ) = $r$ (θ) la corba serà simètrica respecte del radi horitzontal (0°/180°), si $r$ (π−θ) = $r$ (θ) serà simètrica respecte del radi vertical (90°/270°), i si $r$ (θ−α°) = $r$ (θ) tindrà simetria de rotació α° en sentit contrari de les agulles del rellotge al voltant del pol.

A causa de la naturalesa circular del sistema de coordenades polars, moltes corbes es poden descriure amb una equació polar bastant simple, mentre que la seva forma cartesiana és molt més complicada. Entre les més conegudes d'aquestes corbes hi ha la rosa, l'espiral d'Arquimedes, la Lemniscata, el cargol de Pascal, i la cardioide.

Per al cas del cercle, la recta que passa pel pol, i la rosa que s'estudien tot seguit, s'ha d'entendre que no hi ha restriccions ni en el domini ni en el recorregut de les corbes.

Cercle[modifica]

L'equació general d'un cercle amb centre a ( $r$ ₀, φ) i de radi $a$ és

r^{2}-2rr_{0}\cos(\theta -\varphi )+r_{0}^{2}=a^{2}.\,

Això es pot simplificar de diverses maneres, per ajustar-se a casos més específics, com ara l'equació

r(\theta )=a\,

Per al cas d'un cercle amb centre al pol i radi $a$ .^[11]

Recta[modifica]

Les línies rectes Radials (les que passen pel pol) es representen per l'equació

\theta =\varphi \,

,

on φ és l'angle d'elevació de la línia; és a dir, φ = arctan $m$ on $m$ és el pendent de la recta en el sistema de coordenades cartesianes. La recta no radial que talla la recta radial θ = φ perpendicularment al punt ( $r$ ₀, φ) té per equació

r(\theta )={r_{0}}\sec(\theta -\varphi ).\,

Rosa[modifica]

Una rosa és una famosa corba matemàtica que sembla els pètals d'una flor, i que es pot expressar amb una equació polar senzilla,

r(\theta )=a\cos(k\theta +\phi _{0})\,

Per a qualsevol constant $\phi _{0}$ (incloent-hi 0). Si k és un enter, aquestes equacions produeixen una rosa de k pètals si k és senar, o una rosa amb 2k pètals si k és parell. Si k és racional però no és enter, es genera una forma similar a una rosa però amb els pètals encavalcant-se. Fixeu-vos que aquestes equacions mai defineixen una rosa amb 2, 6, 10, 14, etc. pètals. La variable independent a representa la longitud dels pètals de la rosa.

Hèlix[modifica]

Una hèlix és una corba matemàtica que sembla l'hèlix d'un vaixell, i que es pot expressar amb una equació polar senzilla,

r(\theta )=a\exp(\sin(k\theta ))\,

Aquestes equacions produeixen una hèlix de k pales, independentment de si k és parell o senar.

Espiral d'Arquimedes[modifica]

L'espiral d'Arquimedes és una espiral famosa que va ser descoberta per Arquimedes, la qual també es pot expressar amb una equació polar senzilla. Es representa per l'equació

r(\theta )=a+b\theta .\,

Canviant el paràmetre a es fa girar l'espiral, mentre que b controla la distància entre els braços, la qual per una espiral donada és constant. L'espiral d'Arquimedes té dos braços, un per θ > 0 i un altre per θ < 0. Els dos braços es connecten suaument al pol. Prenent la imatge especular d'un braç respecte de la recta de 90°/270° s'obté l'altre braç. Aquesta corba és notable per ser una de les primeres corbes, després de les còniques que es va descriure als tractats de matemàtiques, i per ser el primer exemple d'una corba que es defineix millor per la seva equació polar.

Altres espirals[modifica]

Aquí es pot veure una curiosa funció en coordenades polars, que genera una espiral oscil·latòria del tipus d'Arquimedes, que presenta un període primari de 2k i un secundari de j.

r(\theta )=a\theta +\sin(k\theta )\cdot \cos(j\theta )\,

Còniques[modifica]

Una cònica amb un focus al pol i l'altre en algun lloc del radi de 0° (de forma que el semieix major cau damunt de l'eix polar) ve donada per:

r={\ell  \over {1+e\cos \theta }}

on e és l'excentricitat i $\ell$ és el semi-latus rectum (la distància mesurada sobre la perpendicular a l'eix major que passa pel focus entre el focus i la corba). Si e > 1, aquesta equació defineix una hipèrbola; si e = 1, defineix una paràbola; i si e < 1, defineix una el·lipse. El cas especial de l'el·lipse en què e = 0 en resulta una circumferència de radi $\ell$ .

Nombres complexos[modifica]

Una il·lustració d'un nombre complex representat en el pla complex.

Cada nombre complex es pot representar com un punt del pla complex, i per tant es pot expressar tant especificant les seves coordenades cartesianes (anomenada forma rectangular o cartesiana) com especificant les seves coordenades polars (anomenada la forma polar). El nombre complex z es pot representar en forma rectangular com

z=x+iy\,

on i és la unitat imaginària, o alternativament es pot escriure en forma polar (via la fórmula de conversió donada més amunt) com

z=r\cdot (\cos \theta +i\sin \theta )

I a partir d'aquí com

z=re^{i\theta }\,

on e és la constant d'Euler, les quals són equivalents tal com es demostra per la fórmula d'Euler.^[12] (Fixeu-vos que aquesta fórmula, igual que totes les que impliquen exponencials d'angles, dona per suposat que l'angle s'expressa en radians). Per convertir un complex de la forma rectangular a la polar o viceversa, es poden fer servir les fórmules donades més amunt.

En general, les operacions de multiplicació, divisió, i exponenciació de nombres complexos són molt més fàcils de fer si els nombres s'expressen en notació polar que si s'expressen en notació rectangular. A partir de les lleis de l'exponenciació:

Multiplicació:

r_{0}e^{i\theta _{0}}\cdot r_{1}e^{i\theta _{1}}=r_{0}r_{1}e^{i(\theta _{0}+\theta _{1})}\,

Divisió:

{\frac {r_{0}e^{i\theta _{0}}}{r_{1}e^{i\theta _{1}}}}={\frac {r_{0}}{r_{1}}}e^{i(\theta _{0}-\theta _{1})}\,

Exponenciació (fórmula de De Moivre):

(re^{i\theta })^{n}=r^{n}e^{in\theta }\,

Càlcul[modifica]

El càlcul es pot aplicar a equacions expressades en coordenades polars. En aquesta àrea, la coordenada angular θ s'expressa en radians.

Càlcul diferencial[modifica]

Es tenen les següents fórmules:

r{\tfrac {\partial }{\partial r}}=x{\tfrac {\partial }{\partial x}}+y{\tfrac {\partial }{\partial y}}\,

{\tfrac {\partial }{\partial \theta }}=-y{\tfrac {\partial }{\partial x}}+x{\tfrac {\partial }{\partial y}}.

Per trobar el pendent cartesià de la recta tangent a una corba polar r(θ) a un punt donat qualsevol, primer s'expressa la corba en un sistema d'equacions paramètriques.

x=r(\theta )\cos \theta \,

y=r(\theta )\sin \theta \,

Derivant les dues equacions respecte de θ dona

{\frac {dx}{d\theta }}=r'(\theta )\cos \theta -r(\theta )\sin \theta \,

{\frac {dy}{d\theta }}=r'(\theta )\sin \theta +r(\theta )\cos \theta \,

Dividint la segona equació entre la primera dona el pendent cartesià de la recta tangent a la corba al punt (r, r(θ)):

{\frac {dy}{dx}}={\frac {r'(\theta )\sin \theta +r(\theta )\cos \theta }{r'(\theta )\cos \theta -r(\theta )\sin \theta }}

Càlcul integral[modifica]

Sia R la regió tancada per la corba r(θ) i els radis θ = a and θ = b, on 0 < b − a < 2π. Llavors l'àrea de R és

{\frac {1}{2}}\int _{a}^{b}r(\theta )^{2}\,d\theta .

Aquest resultat es pot obtenir tal com segueix. Primer, l'interval [a, b] es divideix en n subintervals, on n és un enter positiu qualsevol. Per tant Δθ, la longitud de cada subinterval, és igual a b − a (la longitud total de l'interval), dividida entre n, el nombre de subintervals. Per cada subinterval i = 1, 2, …, n, sia θ_i el punt mitjà del subinterval, i es construeix un sector circular amb centre al pol, radi r(θ_i), angle centra Δθ i longitud d'arc $r(\theta _{i})\Delta \theta \,$ . L'àrea de cada un dels sectors que s'ha construït és igual a ${\tfrac {1}{2}}r(\theta _{i})^{2}\Delta \theta$ . Per tant l'àrea total de tots els sectors és

\sum _{i=1}^{n}{\tfrac {1}{2}}r(\theta _{i})^{2}\,\Delta \theta .

A mesura que el nombre de subintervals n creix, l'aproximació de l'àrea millora. En el límit quan n → ∞, el sumatori esdevé el sumatori de Riemann de la integral de més amunt.

Generalització[modifica]

Utilitzant les coordenades cartesianes, un element d'àrea infinitesimal es pot calcular com dA = dx dy. La integració per substitució (o per canvi de variable) per integrals múltiples estableix que cal considerar el determinant del Jacobià de la conversió de coordenades quan hi ha canvi de coordenades. Aquest determinant és:

J=\det {\frac {\partial (x,y)}{\partial (r,\theta )}}={\begin{vmatrix}{\frac {\partial x}{\partial r}}&{\frac {\partial x}{\partial \theta }}\\{\frac {\partial y}{\partial r}}&{\frac {\partial y}{\partial \theta }}\end{vmatrix}}={\begin{vmatrix}\cos \theta &-r\sin \theta \\\sin \theta &r\cos \theta \end{vmatrix}}=r\cos ^{2}\theta +r\sin ^{2}\theta =r.

Per tant, un element d'àrea en coordenades polars es pot escriure com

dA=J\,dr\,d\theta =r\,dr\,d\theta .

Per tant, una funció que es dona en coordenades polars es pot integrar com segueix:

\iint _{R}f(r,\theta )\,dA=\int _{a}^{b}\int _{0}^{r(\theta )}f(r,\theta )\,r\,dr\,d\theta .

Aquí, R és la mateixa regió de més amunt, això és, la regió que està tancada per la corba r(θ) i els radis θ = a i θ = b.

La fórmula de l'àrea R de més amunt s'aconsegueix prenent f igual a 1. Una aplicació d'aquest resultat porta a la integral de Gauß

\int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}.

Càlcul vectorial[modifica]

El càlcul vectorial també es pot aplicar en coordenades polars. Sia $\mathbf {r}$ el vector de posició $(r\cos(\theta ),r\sin(\theta ))\,$ , amb r i $\theta$ en funció del temps t,sia ${\hat {\mathbf {r} }}$ un vector unitari en la direcció $\mathbf {r}$ i sia ${\hat {\boldsymbol {\theta }}}$ un vector unitari perpendicular a $\mathbf {r}$ . Les derivades primera i segona de la posició són

{\frac {d\mathbf {r} }{dt}}={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\theta }}{\hat {\boldsymbol {\theta }}},

{\frac {d^{2}\mathbf {r} }{dt^{2}}}=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}){\hat {\boldsymbol {\theta }}}.

Tres dimensions[modifica]

El sistema de coordenades polars es pot estendre a tres dimensions de dues formes diferents que donen lloc a dos sistemes de coordenades diferents, el sistema de coordenades cilíndriques i el sistema de coordenades esfèriques: tots dos inclouen com subconjunt el sistema de coordenades polar. En essència, el sistema de coordenades cilíndriques estén el sistema de coordenades polar a base d'afegir-li una coordenada addicional de tipus distància, mentre que el sistema de coordenades esfèriques l'estén a base d'afegir-li una coordenada addicional de tipus angular.

Coordenades cilíndriques[modifica]

El sistema de coordenades cilíndriques és un sistema de coordenades que essencialment estén el sistema de coordenades polar bidimensional a base d'afegir-li una tercera coordenada que mesura l'alçada del punt per damunt del pla, de forma similar a com el sistema de coordenades cartesianes s'estén a tres dimensions. Habitualment es denota la tercera coordenada com h, de forma que les tres coordenades cilíndriques són (r, θ, h).

Les tres coordenades cilíndriques es poden transformar en coordenades cartesianes amb

{\begin{aligned}x&=r\,\cos \theta \\y&=r\,\sin \theta \\z&=h.\end{aligned}}

Coordenades esfèriques[modifica]

Les coordenades polars també es poden estendre a tres dimensions fent servir les coordenades (ρ, φ, θ), on ρ és la distància a l'origen, φ és l'angle respecte de l'eix z (anomenat la colatitud o zenit i mesurat des de 0 fins a 180°) i θ és l'angle respecte de l'eix x (com a les coordenades polars). Aquest sistema de coordenades, anomenat sistema de coordenades esfèriques, és similar al sistema basant-se en la latitud i la longitud que es fa servir per determinar els punts a la superfície de la Terra, amb origen al centre de la Terra, la latitud δ és el complement de φ, determinat per δ = 90° − φ, i la longitud l es mesura per l = θ − 180°.^[13]

Les coordenades esfèriques es poden transformar en coordenades cartesianes amb

{\begin{aligned}x&=\rho \,\cos \phi \,\cos \theta \\y&=\rho \,\cos \phi \,\sin \theta \\z&=\rho \,\sin \phi .\end{aligned}}

Aplicacions[modifica]

Les coordenades polars són bidimensionals i per tant només es poden fer servir quan els punts pertanyen a un únic pla bidimensional. Són més apropiades en qualsevol context on el fenomen que es vol estudiar està lligat inherentment a la direcció i la distància respecte d'un punt central. Per exemple, en els casos de més amunt es mostra com equacions polars elementals són suficients per definir corbes -com ara l'espiral d'Arquimedes- per les que l'equació en coordenades cartesianes seria molt més complicada. A més, molts sistemes físics –com ara els relatius a cossos que es mouen entorn d'un punt central o a fenòmens originats a partir d'un punt central — són més senzills i més intuïtius de modelitzar fent servir coordenades polars. El motiu original per la introducció dels sistemes de coordenades polars va ser l'estudi del moviment circular i del moviment orbital.

Posició i navegació[modifica]

Les coordenades polars es fan servir sovint en navegació, atès que la destinació o la direcció del viatge es poden donar com un angle i una distància a partir de l'objecte que s'està considerant. Per exemple, un avió fa servir una versió lleugerament modificada de les coordenades polars per la navegació. En aquest sistema, el radi de 0° se'n diu normalment direcció 360, i els angles segueixen el sentit de les agulles del rellotge en comptes de la direcció contrària d'aquestes, tal com es fa en el sistema matemàtic. La direcció 360 correspon al pol nord magnètic, mentre que les direccions 90, 180 i 270 corresponen a l'est, sud i oest magnètics respectivament.^[14] Així, un avió que viatgi 5 milles nàutiques direcció est estarà viatjant 5 unitats en direcció 90 (pronunciat niner-zero pel servei de control del tràfic aeri).^[15]

Modelització[modifica]

Els sistemes que presenten simetria radial ofereixen un escenari natural pel sistema de coordenades polars, amb el punt central actuant com pol. Un exemple principal d'aquest ús és l'equació de flux d'aigües subterrànies quan s'aplica a pous amb simetria radial. Sistemes amb forces radials són també bons candidats per fer servir els sistemes de coordenades polars. Aquests sistemes inclouen els camps gravitacionals, en què una dada és inversament proporcional al quadrat d'una altra dada, així com sistemes amb fonts puntuals com ara antenes de ràdio.

Els sistemes que són radialment asimètrics també es poden modelitzar fent servi coordenades polars. Per exemple, els patrons polars d'un micròfon il·lustren la seva resposta proporcional a un so entrant provinent d'una direcció donada, i aquests patrons es poden representar com corbes polars. La corba per un micròfon cardioide estàndard, el micròfon unidireccional més comú, es pot representar com r = 0.5 + 0.5 sin θ.^[16] El patró es modifica passant cap a l'omnidireccionalitat a freqüències baixes.

La modelització tridimensional dels patrons de sortida dels altaveus es pot utilitzar per predir les seves prestacions. Calen uns quants diagrames polars dibuixats en una àmplia selecció de freqüències perquè els patrons canvien molt amb la freqüència. Els diagrames polars ajuden a mostrar que molts altaveus tendeixen a comportar-se com omnidireccionals a baixes freqüències.

Vegeu també[modifica]

Referències[modifica]

General

Anton, Howard; Irl Bivens, Stephen Davis. Calculus. Seventh Edition. Anton Textbooks, Inc., 2002. ISBN 0-471-38157-8.
Finney, Ross; George Thomas, Franklin Demana, Bert Waits. Calculus: Graphical, Numerical, Algebraic. Single Variable Version. Addison-Wesley Publishing Co., Juny 1994. ISBN 0-201-55478-X.

Específiques

↑ ^1,0 ^1,1 Brown, Richard G. Andrew M. Gleason. Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis. Evanston, Illinois: McDougal Littell, 1997. ISBN 0-395-77114-5.
↑ Friendly, Michael. «Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization». Arxivat de l'original el 2011-03-20. [Consulta: 10 setembre 2006].
↑ ^3,0 ^3,1 Coolidge, Julian «The Origin of Polar Coordinates». American Mathematical Monthly, 59, 1952, pàg. 78–85.
↑ Boyer, C. B. «Newton as an Originator of Polar Coordinates». American Mathematical Monthly, 56, 1949, pàg. 73–78.
↑ Miller, Jeff. «Earliest Known Uses of Some of the Words of Mathematics». Arxivat de l'original el 1999-10-03. [Consulta: 10 setembre 2006].
↑ Smith, David Eugene. History of Mathematics, Vol II. Boston: Ginn and Co., 1925, p. 324.
↑ «Polar Coordinates and Graphing» (PDF), 13-04-2006. Arxivat de l'original el 2007-09-28. [Consulta: 22 setembre 2006].
↑ Lee, Theodore; David Cohen, David Sklar. Precalculus: With Unit-Circle Trigonometry. Fourth Edition. Thomson Brooks/Cole, 2005. ISBN 0534402305.
↑ Stewart, Ian; David Tall. Complex Analysis (the Hitchhiker's Guide to the Plane). Cambridge University Press, 1983. ISBN 0521287634.
↑ Serway, Raymond A.; Jewett, Jr., John W.. Principles of Physics. Brooks/Cole—Thomson Learning, 2005. ISBN 0-534-49143-X.
↑ Claeys, Johan. «Polar coordinates». Arxivat de l'original el 2006-04-27. [Consulta: 25 maig 2006].
↑ Smith, Julius O. «Euler's Identity». A: Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing, 2003. ISBN 0-9745607-0-7 [Consulta: 22 setembre 2006].
↑ Wattenberg, Frank. «Spherical Coordinates», 1997. Arxivat de l'original el 2013-05-16. [Consulta: 16 setembre 2006].
↑ Santhi, Sumrit. «Aircraft Navigation System». [Consulta: 12 novembre 2006].
↑ «Emergency Procedures». [Consulta: 15 gener 2007].
↑ Eargle, John. Handbook of Recording Engineering. Quarta edició. Springer, 2005. ISBN 0387284702.

Enllaços externs[modifica]

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Coordenades polars

[brown-1] 1,0 ^1,1 Brown, Richard G. Andrew M. Gleason. Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis. Evanston, Illinois: McDougal Littell, 1997. ISBN 0-395-77114-5.

[milestones-2] Friendly, Michael. «Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization». Arxivat de l'original el 2011-03-20. [Consulta: 10 setembre 2006].

[coolidge-3] 3,0 ^3,1 Coolidge, Julian «The Origin of Polar Coordinates». American Mathematical Monthly, 59, 1952, pàg. 78–85.

[4] Boyer, C. B. «Newton as an Originator of Polar Coordinates». American Mathematical Monthly, 56, 1949, pàg. 73–78.

[5] Miller, Jeff. «Earliest Known Uses of Some of the Words of Mathematics». Arxivat de l'original el 1999-10-03. [Consulta: 10 setembre 2006].

[6] Smith, David Eugene. History of Mathematics, Vol II. Boston: Ginn and Co., 1925, p. 324.

[7] «Polar Coordinates and Graphing» (PDF), 13-04-2006. Arxivat de l'original el 2007-09-28. [Consulta: 22 setembre 2006].

[8] Lee, Theodore; David Cohen, David Sklar. Precalculus: With Unit-Circle Trigonometry. Fourth Edition. Thomson Brooks/Cole, 2005. ISBN 0534402305.

[9] Stewart, Ian; David Tall. Complex Analysis (the Hitchhiker's Guide to the Plane). Cambridge University Press, 1983. ISBN 0521287634.

[10] Serway, Raymond A.; Jewett, Jr., John W.. Principles of Physics. Brooks/Cole—Thomson Learning, 2005. ISBN 0-534-49143-X.

[ping-11] Claeys, Johan. «Polar coordinates». Arxivat de l'original el 2006-04-27. [Consulta: 25 maig 2006].

[12] Smith, Julius O. «Euler's Identity». A: Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing, 2003. ISBN 0-9745607-0-7 [Consulta: 22 setembre 2006].

[13] Wattenberg, Frank. «Spherical Coordinates», 1997. Arxivat de l'original el 2013-05-16. [Consulta: 16 setembre 2006].

[14] Santhi, Sumrit. «Aircraft Navigation System». [Consulta: 12 novembre 2006].

[15] «Emergency Procedures». [Consulta: 15 gener 2007].

[16] Eargle, John. Handbook of Recording Engineering. Quarta edició. Springer, 2005. ISBN 0387284702.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]