Teoria de conjunts
La teoria de conjunts és la branca de les matemàtiques que estudia els conjunts. El primer estudi formal sobre el tema va ser realitzat pel matemàtic alemany Georg Cantor al segle xix.
Definició de conjunt[modifica]
Intuïtivament, un conjunt és una agrupació, classe o col·lecció d'objectes, als quals hom anomena elements del conjunt. Així, quan un element a pertany al conjunt S, hom diu que el conjunt S conté l'element a, utilitzant la notació a ∈ S.
La definició de l'accepció matemàtica de la paraula catalana conjunt que dona Pompeu Fabra en el diccionari, coincideix gairebé exactament amb la traducció de l'alemany al català de la definició que va donar el principal creador de la teoria de conjunts, Georg Cantor, al començament de la seva obra Beiträge zur Begründung der transfiniten Mengenlehre:[1]
- S'entén per "conjunt" qualsevol col·lecció M, considerada com un tot, d'objectes, de la nostra percepció [Anschauung] o del nostre pensament, diferents i ben definits m (dels quals se'n dirà els "elements" de M).
El concepte de conjunt és fonamental en matemàtiques, perquè es troba, implícitament o explícita, en totes les branques de les matemàtiques pures i aplicades. En la seva forma explícita, els principis i la terminologia dels conjunts s'utilitzen per a construir proposicions matemàtiques més clares i precises i per a explicar conceptes abstractes, com ara el concepte d'infinit.
Un conjunt S està definit si, donat un objecte qualsevol a, se sap amb seguretat si pertany o no al conjunt.
La paradoxa de Russell[modifica]
Aquesta definició és problemàtica des del punt de vista formal, ja que, en definir un conjunt per una propietat, s'arriba a la paradoxa de Russell definint A = {x|x ∉ x} (es llegeix A està format per tots els elements x tals que x no pertany a x). Veiem que, si A pertany a A, s'ha de complir que A no pertany a A, i que si A no pertany a A, s'ha de complir que A pertany a A: una propietat i la seva negació s'han de complir al mateix temps. Això va portar a considerar desenvolupaments axiomàtics com els de Zermelo-Fraenkel i von Neumann, que eviten aquesta paradoxa o contradicció de la teoria.
Suposem que hi ha dos tipus de conjunts: els normals, que no es contenen a si mateixos com a element; i els anormals, que es contenen a si mateixos com a element. Per a existir, un conjunt A hauria de ser de només d'un dels dos tipus. Pensem ara en el conjunt V els elements del qual són tots els conjunts normals: el conjunt V és normal o anormal? Si V fora normal, es contindria a si mateix com a element, ja que V està format per tots els conjunts normals, però, en contenir-se a si mateix com a element, seria anormal.
La contradicció és deguda al fet de suposar que la proposició "X és un conjunt i no és element de si mateix" determina un conjunt. Hom pensa llavors en dos tipus de col·leccions:
- Classes
- Aquelles col·leccions d'objectes especificades per una proposició.
- Conjunts
- Aquelles classes que siguen elements d'una altra classe.
Hi ha una distinció entre conjunts i classes, en què les classes que no siguin conjunts no poden ser elements d'altres classes. Apareix la teoria axiomàtica de conjunts cercant dos fins: garantir l'existència d'un conjunt i assegurar les construccions amb conjunts que donen com a resultat altres conjunts.
A continuació, s'exposa el desenvolupament intuïtiu de la teoria perquè és el més natural per a la majoria de les persones.
El desenvolupament històric d'una teoria rigorosa de conjunts[modifica]

Cantor va ser el principal creador de la teoria dels conjunts; ho va fer d'una forma que avui es qualifica de teoria ingènua de conjunts. Però, al costat de consideracions elementals, la seva teoria implicava nivells d'abstracció elevats. La verdadera novetat de la teoria de Cantor és que permet parlar de l'infinit. Per exemple, una idea important de Cantor ha estat definir l'equipotència. Dos conjunts A i B són equipotents o, cosa que és el mateix, tenen la mateixa cardinalitat (quan són finits vol dir que tenen el mateix nombre d'elements), si existeix una manera d'associar a cada element de A un i només un element de B i viceversa. Així, es pot demostrar que el conjunt dels naturals té la mateixa cardinalitat que el conjunt dels nombres racionals, encara que sigui un subconjunt propi de . Aquests dos conjunts s'anomenen infinits numerables. D'altra banda, el conjunt dels nombres reals no té la mateixa cardinalitat que o , sinó una cardinalitat superior: es diu que és no numerable. Cantor va donar dues demostracions que no és numerable; la segona d'aquestes demostracions, que fa servir un argument conegut amb el nom d'argument de la diagonal de Cantor, ha estat extraordinàriament influent i ha tingut nombroses i diverses aplicacions en lògica i en matemàtiques.
Cantor va aprofundir en la teoria i va construir jerarquies infinites de conjunts infinits, els nombres ordinals i els nombres cardinals. Aquestes construccions van ser discutides en la seva època; l'oposició principal la mantenia Leopold Kronecker; però avui en dia s'accepten per la majoria dels matemàtics.
El desenvolupament de la teoria de conjunts per Cantor era encara «ingènua» en el sentit que no feia servir encara una axiomàtica precisa, i perquè per a ell no hi havia més que una sola teoria dels conjunts, un sol univers de conjunts esperat, mentre que els teòrics dels conjunts d'avui fan jocs malabars amb universos diferents.
Després, de vegades, s'ha simplificat bastant injustament Cantor, resumint la seva teoria en un ús tàcit de l'axioma d'extensionalitat, i una versió massa forta de l'esquema d'axiomes de comprensió, que en substància permetria associar a tota propietat el conjunt objectes que verifiquen aquesta propietat. Tal teoria, que no s'atribuiria a Cantor, és contradictòria. Porta a dues famílies de paradoxes. Unes, com la paradoxa de Berry o la paradoxa de Richard, es relacionen amb el fet que el llenguatge no està ben definit, les altres, com la paradoxa de Russell a un ús massa ampli de la comprensió: quan s'intenta construir el conjunt S = {A|A no pertany a A} de tots els conjunts que no pertanyen a si mateixos, es cau en una contradicció. L'actual esquema d'axiomes de comprensió, proposat per Zermelo, es restringeix per tal d'evitar aquesta paradoxa.
Cantor coneixia, abans del descobriment de la paradoxa de Russell, paradoxes més complexes, però d'igual naturalesa, com la paradoxa de Burali-Forti o la paradoxa del cardinal més gran.[2] Molts teòrics dels conjunts s'inclinen a dir que l'axiomatització més adequada a la teoria desenvolupada per Cantor és la teoria ZFC amb axioma de fundació (vegeu més avall), o la teoria de les classes de von Neumann, Gödel i Bernays, que és, en un cert sentit (que es pot determinar amb precisió), equivalent.
Al tombant del segle, Cantor està cada vegada més impedit per la seva malaltia nerviosa, però les seves solucions a les paradoxes circulen per la seva correspondència i són conegudes, al final del segle xix, per Richard Dedekind i, a Göttingen, per David Hilbert i Ernst Zermelo. Tanmateix, per a molts matemàtics de l'època, les paradoxes plantegen un dubte sobre la validesa de la teoria dels conjunts; les solucions proposades per Cantor són massa informals per a convèncer els que les coneixen. Alguns s'orienten cap al mètode axiomàtic, il·lustrat a la mateixa època per Hilbert per als fonaments de la geometria (1899).
Així, el 1908, Ernst Zermelo construeix un sistema d'axiomes per a la teoria dels conjunts. Fora de l'axioma d'extensionalitat, aquests axiomes es poden veure com una restricció de la versió contradictòria de l'esquema d'axiomes de comprensió als casos particulars útils, que no permeten deduir les paradoxes. En aquest sistema, s'inclou igualment l'axioma d'elecció (que no té res a veure amb la comprensió), un axioma molt polèmic en aquell temps, amb el qual s'ha demostrat (el 1904) el teorema de Zermelo, i que igualment ha estat fet servir implícitament per Cantor. El sistema de Zermelo es va completar en els anys 1920 per Abraham Adolf Fraenkel i Thoralf Skolem, que afegiran l'esquema d'axiomes de substitució (altre cas particular de la comprensió no restringida), que dona la teoria coneguda avui sota el nom de ZF (sense axioma d'elecció) o ZFC (amb l'axioma d'elecció). Altres autors han treballat sobre el problema de l'axiomatització de la teoria dels conjunts, sobretot John Von Neumann, que va definir una alternativa molt interessant a ZF: la teoria de les classes.
Notació[modifica]
Un conjunt es representa mitjançant claus que contenen els seus elements, ja siga de manera explícita, escrivint tots i cada un dels elements, o donant una fórmula, regla o proposició que els descriga. Per exemple,
- S1 = {2, 4}
- S₂ = {2, 4, 6, ...} = {tots els enters parells més grans que 1}
- S₃ = {x|}.
- S₄ = {tots els barons vius anomenats Joan}
La definició de S₃ es llegeix "el conjunt de totes les x tals que ".
Conceptes en teoria de conjunts[modifica]
Subconjunts i superconjunts[modifica]
Si tot element d'un conjunt R pertany també al conjunt S, es diu que R és un subconjunt de S i que S és un superconjunt de R. S'utilitza la notació R ⊆ S. Tot conjunt és un subconjunt i un superconjunt de si mateix.
Si R ⊆ S i almenys un element de S no pertany a R, es diu que R és un subconjunt propi de S i que S és un superconjunt propi de R. S'utilitza la notació R ⊂ S.
Si R ⊆ S i S ⊆ R, és a dir, tot element d'un conjunt pertany també a l'altre, llavors R i S són dos conjunts iguals, la qual cosa s'escriu R = S. En els exemples de l'apartat anterior, S1 = S₃.
Unió i intersecció[modifica]
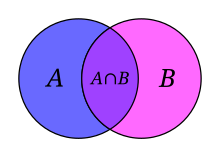
Siguen A i B dos conjunts.
Els elements que pertanyen a A, a B o a ambdós formen un altre conjunt S, anomenat unió de A i B, escrit A ∪ B.
Els elements comuns a A i B formen un conjunt denominat intersecció de A i B, escrit A ∩ B.
Si A i B no tenen cap element comú es denominen conjunts disjunts i es representa la seva intersecció com un altre conjunt, denominat conjunt buit o nul, el qual es representa amb el símbol Ø.
Exemples: si tenim els conjunts:
Llavors:
Diferència i complementari[modifica]
El conjunt d'elements que pertanyen a A però no pertanyen a B es denomina conjunt diferència entre A i B, escrit A – B (i a vegades A \ B).
Seguint amb l'exemple anterior, A – B = {2}, B – A = {8, 10}.
Si A és un subconjunt del conjunt B, el conjunt dels elements que pertanyen a B però no a A, és a dir, B – A, es denomina conjunt complementari de A (respecte a B), la qual cosa s'escriu B – A = AC (que també pot aparèixer com à o ~A).
Àlgebra de conjunts[modifica]
Siguen A, B i C conjunts qualssevol, i U un conjunt tal que A ⊆ U, B ⊆ U i C ⊆ U. Aleshores:
- Element neutre de la unió
- Element neutre de la intersecció
- Propietat commutativa de la intersecció
- Propietat commutativa de la unió
- Propietat associativa de la intersecció
- Propietat associativa de la unió
- Propietat distributiva de la intersecció
- Propietat distributiva de la unió
- Definició
Distributivitat entre unió i intersecció[modifica]
Siguen tres conjunts A, B i C. Es compleix que:
Aquestes són les propietats de l'àlgebra de conjunts, la qual és un cas particular del sistema algebraic conegut com a àlgebra de Boole.
Producte cartesià de conjunts[modifica]
Si A i B són dos conjunts, el conjunt de tots els possibles parells ordenats d'elements de la forma (a, b), en què a ∈ A i b ∈ B, es denomina producte cartesià de A i B, escrit normalment com A × B.
Exemple: si A = {1, 2} i B = {x, y, z}, llavors
En aquest cas, , perquè en ser parells ordenats, el parell (1, x) és diferent del parell (x, 1).
Correspondència o relacions entre conjunts[modifica]
Donats dos conjunts A i B, podem trobar diverses maneres de relacionar els elements de A amb els elements de B.
Per exemple, els elements del conjunt A = {1, 2, 3} es poden relacionar o fer correspondre mitjançant una correspondència f amb els elements del conjunt B = {x, y, z}, de manera que a tot element de A li corresponga un, cap o diversos elements de B. Això també es pot expressar així:
- , ,
També es pot dir que .
Per tant, una relació o correspondència entre dos conjunts A i B és un subconjunt del producte cartesià A × B. Noteu que això inclou el cas del conjunt buit.
Una correspondència tal que a cada element del primer conjunt li'n correspon un i només un del segon conjunt s'anomena aplicació o funció.
El problema de l'axioma d'elecció[modifica]
L'axioma d'elecció va aparèixer explícitament en una publicació d'Ernst Zermelo del 1904; és a dir, abans de l'aparició de la seva axiomatització de la teoria dels conjunts. L'axioma d'elecció és, en efecte, d'una naturalesa diferent dels altres axiomes de la teories dels conjunts enunciats ulteriorment, i que resulten per a la majoria d'una anàlisi detallada de l'esquema d'axiomes d'especificació. En efecte, l'axioma d'elecció no dona cap definició explícita del conjunt construït (conjunt d'elecció o funció d'elecció, segons les versions). D'altra banda, al seu article del 1904, Zermelo demostra amb l'axioma d'elecció el seu famós teorema que enuncia que tot conjunt pot ser ben ordenat, proposició que no té res d'intuïtivament evident. L'axioma d'elecció va ser utilitzat tàcitament almenys per Georg Cantor, però la publicació de Zermelo posa en marxa debats apassionats amb els matemàtics de l'època.[3]
L'axioma d'elecció està, d'altra banda, molt vinculat a l'infinit matemàtic; en efecte, l'axioma d'elecció és intuïtivament verdader per a un nombre finit d'eleccions, i d'altra banda demostrable, en aquest cas, a partir dels altres axiomes de la teoria dels conjunts. Ara bé, al voltant del 1904, entrem de ple en la controvèrsia posada en marxa pel descobriment de les paradoxes.[4] Llavors, diverses concepcions de l'infinit matemàtic s'enfronten. Això arribarà, fins i tot, a qüestionar radicalment els fonaments de les matemàtiques per part de Luitzen Egbertus Jan Brouwer, fundador de l'intuïcionisme, que descarta el principi del terç exclòs, que se situa força més amunt de l'axioma d'elecció. Tanmateix, en aquell temps, certs matemàtics que no van tan lluny i accepten certes formes de raonament no constructiu, desconfien de l'axioma d'elecció. Émile Borel escriu el 1950:[5] És ja un resultat important obtingut pels adversaris de l'axioma de Zermelo que tots els que admeten aquest axioma prenen la cura, quan obtenen un teorema nou, d'especificar si la demostració d'aquest teorema exigeix o no la utilització de l'axioma de Zermelo. Aquest axioma ha creat així una branca separada de les matemàtiques; la importància i l'interès d'aquesta branca decidiran la seva sort. En tot cas, es pot dir que avui, vista justament la seva utilització en branques importants de les matemàtiques, l'axioma d'elecció és àmpliament acceptat.
Això encara més des que se sap, a partir dels treballs de Gödel,[6] que admetre l'axioma d'elecció ja no és «arriscat», en el sentit que demostra que si la teoria ZFC fos incoherent, la teoria ZF també ho seria (vegeu la secció sobre els resultats d'independència en teoria dels conjunts).
D'altra banda, s'han identificat restriccions de l'axioma d'elecció, com l'axioma d'elecció enumerable (que permet, per exemple, demostrar que una reunió numerable de conjunts numerables és numerable); aquest mateix és conseqüència de l'axioma d'elecció depenent (que permet, per exemple, demostrar l'existència d'una successió infinita decreixent per a una relació no ben fonamentada). Així, Robert Solovay va publicar el 1970 la coherència de la teoria ZF + l'axioma d'elecció depenent + tot subconjunt dels reals és Lebesgue-mesurable, teoria que contradiu l'axioma d'elecció en tota la seva generalitat, relativament a la teoria ZF + existeix un cardinal inaccessible (un reforç de la teoria ZF que permet demostrar la coherència de ZF).[7] Tanmateix, l'axioma d'elecció enumerable és insuficient en geometria algebraica, ja que el tractament dels cossos algebraicament tancats requereix el lema de Zorn, que és equivalent a l'axioma d'elecció; per tant, el teorema segons el qual tot cos pot ser submergit en un cos algebraicament tancat es basa en l'axioma d'elecció general.[8]
Un dels millors exemples de les rareses a què condueix l'axioma d'elecció és certament la paradoxa de Banach-Tarski, publicada el 1924[9] que, fent servir l'axioma d'elecció, afirma que es pot tallar una esfera en un nombre finit de trossos, desplaçar-los per una successió de moviment rígids (translació i rotació), tot permetent a certes peces travessar-ne d'altres i reunir-los altre cop formant dues còpies de l'esfera original. Això sembla contradir la intuïció física que es té de la noció de volum, però la paradoxa de Banach-Tarski fa intervenir parts no mesurables.
Axiomes de la teoria de conjunts[modifica]
Els sistemes axiomàtics de la teoria de conjunts, el ZF, la teoria de classes i la teoria dels tipus són equivalents pel cap baix, en el sentit que tots permeten representar l'essència de les matemàtiques. Entre aquests, el ZF és el més habitual i és el que es descriu de manera informal tot seguit.
La teoria que es basa en els axiomes originals de Zermelo s'anomena teoria de Zermelo o teoria Z. Si es completa amb l'axioma de reemplaçament de Fraenkel, s'obté la teoria de Zermelo-Fraenkel, o més simplement la teoria ZF, encara que la forma final dels axiomes és deguda a Skolem. Quan se li assigna l'axioma d'elecció, llavors s'obté la teoria ZFC («C» per 'elecció', que és «choice» en anglès).
Un aspecte important de la teoria ZF és que tots els objectes de què tracta són conjunts i no poden ser més que conjunts. En particular, cada element d'un conjunt també és un conjunt. Altres objectes matemàtics familiars, tals com els nombres, han de ser definits, per tant, en termes de conjunts.
Estrictament parlant, els axiomes de ZF són simplement enunciats del càlcul dels predicats del primer ordre, equivalent a un llenguatge que té un sol símbol primitiu per a la pertinença (relació binària). Per tant, el que segueix s'ha d'entendre només com una temptativa d'expressar en català el significat que s'espera d'aquests axiomes. És més, l'axioma de separació (o comprensió) i l'axioma de substitució són, de fet, esquemes infinits d'axiomes.
- Axioma d'extensionalitat: si dos conjunts tenen els mateixos elements, llavors són idèntics.
- Axioma del conjunt buit: existeix un conjunt sense cap element. Es nota (o menys freqüentment ). Parlant en propietat, Aquest axioma no forma part de l'axiomatització de ZF, pel cap baix en la seva versió actual, formalitzada en càlcul de predicats de primer ordre. Es pot deduir d'una propietat genèrica del càlcul de predicats, que és que un model d'una teoria és no buit. En el cas de la teoria dels conjunts, això significa dir que existeix almenys un conjunt, i aquesta propietat no requereix cap axioma específic: es demostra en lògica pura. D'aquí es dedueix, per l'esquema d'axiomes de comprensió, l'existència del conjunt buit. Tanmateix, aquest axioma es troba en variants de la teoria dels conjunts, o en presentacions més antigues o semiformals de la teoria ZF, com a la de Paul Halmos.[10]
- Axioma d'aparellament: si x i y són dos conjunts; llavors, existeix un conjunt que conté x i y i només aquests com a elements. Aquest conjunt es nota . Cal observar que x i y no són necessàriament diferents. Aquest axioma és conseqüència de l'esquema de substitució, però no de l'esquema de comprensió; també se'l pot ometre en la teoria ZF, però és indispensable en la teoria Z.
- Axioma de reunió: per a tot conjunt X, existeix un conjunt R els elements del qual són precisament els elements dels elements de X i només aquests.
- Axioma del conjunt de les parts: per a tot conjunt E, existeix un conjunt els elements del qual són precisament els subconjunts d'E. Aquest conjunt es nota habitualment .
- Axioma de l'infinit: existeix un conjunt W tal que és element seu i tal que per a tot x que pertany a W, pertany també a W. Llavors, es pot definir per comprensió la intersecció de tots els conjunts que contenen i són tancats respecte d'aquesta operació: es tracta del conjunt dels nombres naturals tals com els defineix von Neumann.
- Esquema d'axiomes de comprensió o de separació: per a tot conjunt A i per a tota propietat P expressada en el llenguatge, existeix un conjunt els elements del qual són els elements de A que verifiquen P. L'esquema de comprensió és conseqüència de l'esquema de substitució que segueix.
- Esquema d'axiomes de substitució: per a tot conjunt A i per a tota relació funcional P, formalment definida com una proposició tal que i impliquen que , existeix un conjunt que conté precisament les imatges per a P dels elements del conjunt d'origen A.
- Axioma de regularitat: tot conjunt X no buit conté un element y tal que X i y són conjunts disjunts (que no tenen cap element en comú), cosa que es nota . Aquest axioma s'afegeix molt sovint a Z o ZF. Es pot construir bastant fàcilment com a subclasse d'un model qualsevol de ZF, un model de ZF que verifica l'axioma de regularitat. Els conjunts útils per al desenvolupament de les matemàtiques usuals pertanyen a aquesta subclasse, i per tant té poca importància afegir o no aquest axioma a la teoria per a aquests desenvolupaments. L'axioma de regularitat, per exemple, no es menciona en el llibre de Halmos,[10] l'objectiu del qual és el de presentar els aspectes de la teoria dels conjunts útils per al matemàtic no especialista d'aquest àmbit. L'axioma de regularitat, en canvi, és molt útil en l'àmbit especialitzat de la teoria de conjunts; permet jerarquitzar l'univers de conjunts, definir un rang ordinal... Per altra banda, s'han desenvolupat teories dels conjunts, extensions de ZF sense regularitat; aquestes teories introdueixen un axioma d'antiregularitat (n'existeixen diverses variants) que contradiu directament l'axioma de regularitat. L'antiregularitat és una idea bastant antiga (Dmitri Mirimanoff, 1917, Paul Finsler, 1926), però aquestes teories han conegut una recuperació d'interès per la seva relació amb la informàtica teòrica.[11]
- Axioma d'elecció: (versió de Zermelo) donat un conjunt X de conjunts no buits mútuament disjunts, existeix un conjunt y (el conjunt d’elecció per X) que conté exactament un element per a cada membre de X.
L'axioma d'elecció continua sent discutit per una minoria de matemàtics. N'hi ha formes febles, com l'axioma d'elecció dependent, molt útil per al desenvolupament de l'anàlisi real.
Aplicacions[modifica]
Gairebé tots els conceptes matemàtics es defineixen avui en dia formalment en termes de conjunts i conceptes teòrics de teoria de conjunts. Per exemple, estructures matemàtiques tan diverses com grafs, varietats (matemàtiques), anells (matemàtics), i espais vectorials es defineixen completament com a conjunts que tenen diverses propietats (axiomes). La relació d'equivalència i les relacions d'ordre són ubiqües en matemàtiques, i la teoria de relacions es basa totalment en la teoria de conjunts.
La teoria de conjunt és també un sistema prometedor per a fonamentar la majoria de les matemàtiques. Des de la publicació del primer volum de Principia Mathematica, s'ha afirmat que molts o fins i tot tots els teoremes matemàtics es poden demostrar fent servir un conjunt dissenyat de manera adequada d'axiomes amb la teoria de conjunts, augmentada amb moltes definicions, fent servir lògica de primer ordre o de segon ordre. Per exemple, les propietats dels nombres naturals i dels nombres reals es poden obtenir dins de la teoria de conjunts, ja que cada sistema de nombres es pot identificar amb un conjunt de classes d'equivalència sota una relació d'equivalència adequada el camp de la qual és algun conjunt infinit.
La teoria de conjunts com a fonament per a l'anàlisi matemàtica, la topologia, l'àlgebra abstracta, i les matemàtiques discretes és de la mateixa manera incontrovertida; els matemàtics accepten que (en principi) els teoremes en aquestes àrees poden ser deduïts de les definicions pertinents i els axiomes de la teoria de conjunts. S'han verificat formalment poques deduccions completes de teoremes matemàtics complexos a partir de la teoria de conjunts, tanmateix, perquè tals deduccions formals són sovint molt més llargues que el llenguatge natural amb el qual els matemàtics presenten habitualment les demostracions.
Referències[modifica]
- ↑ Quoted in Dauben, p. 170.
- ↑ il ne considère d'ailleurs pas ceux-ci comme des paradoxes, voir le §2.2 de, Akihiro Kanamori (2008), Set Theory from Cantor to Cohen, to appear in: Andrew Irvine and John H. Woods (editors), The Handbook of the Philosophy of Science, volume 4, Mathematics, Cambridge University Press 2008.
- ↑ On trouve dans les leçons sur la théorie des fonctions d'Émile Borel Gauthiers-Villars 4ème édition 1950, un échange de lettres à ce sujet entre René Baire, Jacques Hadamard, Henri Lebesgue et Borel lui-même; les lettres apparaissent dans la note IV introduite à partir de la seconde édition).
- ↑ le paradoxe de Russell et d'autres, est paru dans les principles of mathematics du dit Russell en 1903, le paradoxe de Richard est publié en 1905 ...
- ↑ Préface de la 4ème édition des leçons sur la théorie des fonctions
- ↑ Kurt Gödel. The Consistency of the Axiom of Choice and of the Generalized Continuum Hypothesis with the Axioms of Set Theory, Princeton University Press.ISBN 0-691-07927-7
- ↑ Robert M. Solovay A model of set theory in which every set of reals is Lebesgue mesurable, Annals of Math. 92, 1970, pp 1-56.
- ↑ Ouvrage collectif Penser les mathématiques (séminaire de l'ENS) Editions du Seuil, Paris 1982 ISBN 2 02 006061 2 note 7 p.35
- ↑ Stefan Banach and Alfred Tarski, Sur la décomposition des ensembles de points en parties respectivement congruentes, Fundamenta Mathematicae, 6, (1924), 244–277. Review at JFM
- ↑ 10,0 10,1 Paul Richard Halmos, Naive Set Theory, D. Van Nostrand Company, Princeton, NJ, 1960. Reprinted, Springer-Verlag, New York, NY, 1974, ISBN 0-387-90092-6. trad. Française Introduction à la théorie des ensembles, Gauthier-Villars Paris 1965.
- ↑ voir le livre de Peter Aczel, Non-Well-Founded Sets, CSLI Lecture Notes, Vol.14, CSLI Publications, Stanford, California, 1988.
Vegeu també[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Teoria de conjunts |


























































