Biga (construcció)
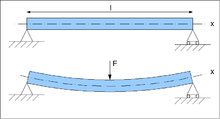
En enginyeria i arquitectura es denomina biga a un element constructiu lineal que treballa principalment a flexió. A les bigues la longitud predomina sobre les altres dues dimensions i sol ser horitzontal. L'esforç de flexió provoca tensions de tracció i compressió, produint-se les màximes al cordó inferior i al cordó superior respectivament, les quals es calculen relacionant el moment flector i el segon moment d'inèrcia. A les zones properes als suports es produeixen esforços tallants o punxonament. També poden produir-se tensions per torsió, sobretot a les bigues que formen el perímetre exterior d'un forjat. Estructuralment el comportament d'una biga s'estudia mitjançant un model de prisma mecànic.[1]
Teoria de bigues d'Euler-Bernoulli[modifica]

La teoria de bigues és una part de la resistència dels materials que permet el càlcul d'esforços i deformacions en bigues. Si bé les bigues reals són sòlids deformables, en teoria de bigues es fan certes simplificacions gràcies a les quals es poden calcular aproximadament les tensions, desplaçaments i esforços a les bigues com si fossin elements unidimensionals.
Els inicis de la teoria de bigues es remunten al segle xviii, treballs que van ser iniciats per Leonhard Euler i Daniel Bernoulli. Per a l'estudi de bigues es considera un sistema de coordenades en les quals l'eix X és sempre tangent a l'eix baricèntric de la biga, i els eixos Y i Z coincideixin amb els eixos principals d'inèrcia. Els supòsits bàsics de la teoria de bigues per a la flexió simple d'una biga que flecte en el pla XY són:
- Hipòtesi de comportament elàstic. El material de la biga és elàstic lineal, amb Mòdul de young E i coeficient de Poisson menyspreable.
- Hipòtesi de la fletxa vertical. En cada punt el desplaçament vertical només depèn de x : uy (x' i) = w (x).
- Hipòtesi de la fibra neutra. Els punts de la fibra neutra només sofreixen desplaçament vertical i gir: ux (x, 0) =0.
- La tensió perpendicular a la fibra neutra s'anul·la: σyy =0.
- Hipòtesi de Bernoulli. Les seccions planes inicialment perpendiculars a l'eix de la biga, continuen sent perpendiculars a l'eix de la biga una vegada corbada.
Les hipòtesis (1)- (4) juntes defineixen la teoria de bigues de Timoshenko. La teoria d'Euler-Bernoulli és una simplificació de la teoria anterior, en acceptar-se l'última hipòtesi com a exacta (quan en bigues reals és només aproximadament certa). El conjunt d'hipòtesi (1)- (5) porta a la següent hipòtesi cinemàtica sobre els desplaçaments:
Deformacions i tensions en bigues[modifica]
Si es calculen els components del tensor de deformacions a partir d'aquests desplaçaments s'arriba a:
A partir d'aquestes deformacions es poden obtenir les tensions usant les Equacions de Lamé-hooke, assumint :
On E és el mòdul d'elasticitat longitudinal, o mòdul de Young, i G el mòdul d'elasticitat transversal. És clar que la teoria d'Euler-Bernoulli és incapaç d'aproximar l'energia de deformació tangencial, per a tal fi s'ha recórrer a la teoria de Timoshenko en la qual:
Esforços interns en bigues[modifica]
a partir dels resultats anteriors i de les equacions d'equivalència poden obtenir-se senzillament l'esforç normal, l'esforç tallant i el moment flector al que està sotmesa una secció d'una biga sotmesa a flexió simple en la teoria d'Euler-Bernoulli:
On: A àrea de la secció transversal, Iz el moment d'inèrcia segons l'eix respecte al qual es produeix la flexió. L'última d'aquestes equacions és precisament l'equació de la corba elàstica, una de les equacions bàsiques de la teoria de bigues que relaciona els esforços interns amb el camp de desplaçaments verticals.
Equacions d'equilibri[modifica]
Les equacions d'equilibri per a una biga són l'aplicació de les equacions de l'estàtica a un tram de biga en equilibri. Les forces que intervenen sobre el tram serien la càrrega exterior aplicada sobre la biga i les forces tallants actuants sobre les seccions extremes que delimiten el tram. Si el tram està en equilibri això implica que la suma de forces verticals ha de ser zero, i a més la suma de moments de força a la fibra neutra ha de ser zero en la direcció tangent a la fibra neutra. Aquestes dues condicions només es poden complir si la variació d'esforç tallant i moment flector estan relacionada amb la càrrega vertical per unitat de longitud mitjançant:
Càlcul de tensions en bigues[modifica]
El càlcul de tensions en bigues generalment requereix conèixer la variació dels esforços interns i a partir d'ells aplicar la fórmula adequada segons la biga estigui sotmesa a flexió, torsió, esforç normal o esforç tallant. El tensor tensió d'una biga ve donat en funció dels esforços interns per:
On les tensions poden determinar-se, aproximadament, a partir dels esforços interns. Si es considera un sistema d'eixos principals d'inèrcia sobre la biga, considerada com a prisma mecànic, les tensions associades a l'extensió, flexió, tallant i torsió resulten ser:
On:
- són les tensions sobre la secció transversal: tensió normal o perpendicular, i les tensions tangencials de torsió i tallant.
- , són els esforços interns: esforç axial, moments flectors i bimoment associat a la torsió.
- , son propietats de la secció transversal de la biga: àrea, moments d'inèrcia, guerxesa i moment d'aquesta.
Les tensions màximes sobre una secció transversal qualsevol de la biga poden al seu torn ser calculades en termes d'aquests components del tensor tensió:

En bigues metàl·liques freqüentment s'usa com a criteri d'error el que en algun punt la Tensió Equivalent De Von Mises superi una certa tensió última definida a partir del límit elàstic, en aquest cas, el criteri d'error es pot escriure com a:
Materials utilitzats[modifica]

Al llarg de la història, les bigues s'han realitzat de diversos materials; el més idoni dels materials tradicionals ha estat la fusta, ja que pot suportar grans esforços de tracció, la qual cosa no succeeix amb altres materials tradicionals petris i ceràmics, com el maó. La fusta tanmateix és un material ortotròpic que presenta diferents rigideses i resistències segons els esforços aplicats siguin paral·lels a la fibra de la fusta o transversals. Per aquesta raó, el càlcul modern d'elements de fusta requereix sota demandes complexes un estudi més complet que la teoria de Navier-Bernoulli, anteriorment exposada.
A partir de la revolució industrial, les bigues es van fabricar en acer, que és un material isòtrop al qual pot aplicar-se directament la teoria de bigues d'Euler-Bernoulli. L'acer té l'avantatge de ser un material amb una relació resistència/pes superior a la del formigó, a més del qual pot resistir tant traccions com compressions molt més elevades. A partir de la segona meitat del segle xix, en arquitectura, s'ha vingut usant formigó armat i una mica més tardanament el formigó pretesat i posttesat. Aquests materials requereixen per al seu càlcul una teoria més complexa que la teoria d'Euler-Bernoulli.
Modernament es van desenvolupar bigues de fusta laminada encolada que en llum (fins a 60 metres i enllà), resistència mecànica i resistència al foc equivalen o superen les bigues d'acer i de formigó.[2] A més tenen un bilanci ecològic superior a l'acer i el formigó.[3]
Referències[modifica]
- ↑ Diccionario de Arte II (en castellà). Barcelona: Biblioteca de Consulta Larousse. Spes Editorial SL (RBA), 2003, p.295. DL M-50.522-2002. ISBN 84-8332-391-5 [Consulta: 8 desembre 2014].
- ↑ «Producció de bigues estructurals amb fusta de frondoses nobles d’origen català». Institut català de la fusta – Incafust, 07-03-2013. [Consulta: 20 agost 2021].
- ↑ Fountain, Henry «Towers of Steel? Look Again» (en anglès). The New York Times, 23-09-2013, pàg. 6. ISSN: 0362-4331.
Vegeu també[modifica]
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Biga |
- Prontuario de sol·licitacions i deformacions en bigues Arxivat 2009-12-23 a Wayback Machine.
- Teoria de bigues (eFunda)
- cabierta.uchile.cl: Bigues de pes mínim Arxivat 2007-06-04 a Wayback Machine.








![{\displaystyle [T]_{xyz}={\begin{bmatrix}\sigma &\tau _{y}&\tau _{z}\\\tau _{y}&0&0\\\tau _{z}&0&0\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57749131647d2a4a8b7d3a9ffe76c29c689178ce)







