Hipergraf

Exemple d'un hipergraf, en el qual $V=\{v_{1},v_{2},v_{3},v_{4},v_{5},v_{6},v_{7}\}$ i $E=\{e_{1},e_{2},e_{3},e_{4}\}=$ $\{\{v_{1},v_{2},v_{3}\},$ $\{v_{2},v_{3}\},$ $\{v_{3},v_{5},v_{6}\},$ $\{v_{4}\}\}$.

En matemàtiques, i més concretament en teoria de grafs, un hipergraf és una generalització d'un graf en la qual les arestes poden connectar un nombre qualsevol de vèrtexs. Formalment, un hipergraf $G$ és un parell de conjunts $G=(V,E)$, on $V$ és el conjunt d'elements anomenat nodes o vèrtexs i $E$ és un conjunt de subconjunts no-buits de $V$ anomenats hiperarestes o simplement arestes. Per tant, $E$ és un subconjunt de ${\mathcal {P}}(V)\setminus \{\emptyset \}$, on ${\mathcal {P}}(V)$ és el conjunt de les parts de $V$.

Mentre que les arestes d'un graf són parells de vèrtexs, les hiperarestes són conjunts arbitraris de vèrtexs, i per tant poden contenir un nombre arbitrari de vèrtexs. Tanmateix, sovint és interessant estudiar hipergrafs on totes les hiperarestes tenen la mateixa cardinalitat; un hipergraf k-uniforme és un hipergraf on totes les hiperarestes tenen grandària k (en altres paraules, un tal hipergraf és una col·lecció de conjunts, on cadascun representa una hiperaresta que connecta k vèrtexs). Així, un hipergraf 2-uniforme és un graf, un hipergraf 3-regular és una col·lecció de triplets no ordenats, i així successivament.

Un hipergraf també es coneix com a sistema de conjunts o una família de conjunts escollits del conjunt universal X. La diferència entre un sistema de conjunts i un hipergraf és una qüestió encara ni tancada. La teoria d'hipergrafs tendeix a tractar qüestions simulars a les de la teoria de grafs, com la connectivitat o la coloració, mentre que la teoria de sistemes de conjunts acostuma a tractar aspectes no relacionats amb la teoria de grafs, com a la teoria de Sperner.

Existeixen diferents definicions per als hipergrafs; de vegades les arestes han de ser no buides, i de vegades es permeten arestes múltiples, que connecten el mateix conjunt de vèrtexs.

Els hipergrafs es poden veure com a estructures d'incidència. En particular, existeix un "graf d'incidència" o "graf de Levi" corresponent a cada hipergraf; recíprocament, la majoria de grafs bipartits, però no qualsevol, es poden interpretar com a grafs d'incidència d'hipergrafs.

Els hipergrafs tenen altres noms. En geometria computacional, un hipergraf es pot conèixer com a espai de rangs i les hiperarestes s'anomenen rangs. En teoria de jocs cooperatius, els hipergrafs es coneixen com a jocs simples (jocs de votació); aquesta noció s'aplica en la resolució de problemes de teoria de l'elecció social. Alguns autors es refereixen a les hiperarestes com a hiperenllaços o connectors.

Alguns tipus especials d'hipergrafs inclouen, a part dels k-uniformes, els clutters, on cap aresta apareix com a subconjunt de cap altra aresta; i els complexos simplicials abstractes, que contenen tots els subconjunts de cada aresta.

La col·lecció dels hipergrafs és una categoria amb homomorfismes d'hipergrafs com a morfismes.

Terminologia

Com que les arestes d'un hipergraf poden tenir qualsevol cardinalitat, existeixen diferents nocions sobre el concepte de subgraf, anomenades subhipergrafs, hipergrafs parcials i hipergrafs de secció.

Sigui $H=(X,E)$ l'hipergraf que consisteix dels vèrtexs

$X=\lbrace x_{i}|i\in I_{v}\rbrace ,$

i amb el conjunt d'arestes

$E=\lbrace e_{i}|i\in I_{e},e_{i}\subseteq X\rbrace ,$,

on $I_{v}$ i $I_{e}$ són els conjunts d'índexs dels vèrtexs i de les arestes, respectivament.

Un subhipergraf és un hipergraf on s'han eliminat alguns dels vèrtexs. Formalment, el subhipergraf $H_{A}$ induït per un subconjunt $A$ de $X$ es defineix com

$H_{A}=\left(A,\lbrace e_{i}\cap A|e_{i}\cap A\neq \varnothing \rbrace \right)$.

L'hipergraf parcial és un hipergraf on s'han eliminat algunes arestes. Donat un subconjunt $J\subset I_{e}$ del conjunt d'índexs de les arestes, l'hipergraf parcial generat per $J$ és l'hipergraf

$\left(X,\lbrace e_{i}|i\in J\rbrace \right)$.

Donat un subconjunt $A\subseteq X$, l'hipergraf de secció és l'hipergraf parcial

$H\times A=\left(A,\lbrace e_{i}|i\in I_{e},e_{i}\subseteq A\rbrace \right)$.

El dual $H^{*}$ de $H$ és un hipergraf on s'han intercanviat els vèrtexs amb les arestes, de tal manera que els vèrtexs venen donats per $\lbrace e_{i}\rbrace$ i les arestes del qual venen donades per $\lbrace X_{m}\rbrace$, on

$X_{m}=\lbrace e_{i}|x_{m}\in e_{i}\rbrace$.

Quan es proporciona una noció d'igualtat definida adequadament, com es fa més endavant, l'operade passar al dual d'un hipergraf és una involució, és a dir,

$\left(H^{*}\right)^{*}=H$.

Un graf connex G amb el mateix conjunt de vèrtexs d'un hipergraf connex H és un graf histe de H si tota hiperaresta de H indueix un subgraf connex dins G. En el cas d'un hipergraf no connex H, G és un graf hoste si existeix una bijecció entre les components connexes de G i les de H, de tal manera que cada component connexa G' de G és un hoste de la corresponent H'.

Un hipergraf és bipartit si i només si els seus vèrtexs admeten una partició en dues classes U i V de tal manera que cada hiperaresta amb cardinalitat ≥2 conté, almenys, un vèrtex de cadascuna de les classes.

La 2-secció (o graf «clique», graf representant, graf primari, graf de Gaifman) d'un hipergraf és un graf amb els mateixos vèrtexs de l'hipergraf, i amb les arestes entre tots els parells de vèrtexs continguts en la mateixa hiperaresta.

Model de graf bipartit

Un hipergraf H es pot representar mitjançant un graf bipartit BG de la següent forma: els conjunts X i E són les particions de BG, i (x₁, e₁) estan connectats per una aresta si i només si el vèrtex x₁ està contingut en l'aresta e₁ de H. Recíprocament, tot graf bipartit sense vèrtexs aïllats es pot descriure de la forma anterior. Aquest graf bipartit es coneix també com a graf d'incidència.

Aciclicitat

En contrast amb els grafs no dirigits ordinaris, on existeix una única noció natural de cicles i grafs acíclics, existeixen diverses definicions naturals, no equivalents entre si, d'aciclicitat per a hipergrafs, que esdevenen l'aciclicitat ordinària de grafs en el cas especial que l'hipergraf sigui, de fet, un graf.

Una primera definició d'aciclicitat per a hipergrafs fou establerta per Claude Berge: un hipergraf és Berge-acíclic si el seu graf d'incidència (el graf bipartit definit abans) és acíclic. Aquesta definició és molt restrictiva: per exemple, si un hipergraf té un parell $v\neq v'$ de vèrtexs i un parell $f\neq f'$ d'hiperarestes tals que $v,v'\in f$ i $v,v'\in f'$, llavors és Berge-cíclic. La ciclicitat en el sentit de Berge es pot comprovar en temps lineal mitjançant l'exploració del graf d'incidència.

Hom pot definir una noció més feble d'hipergrafs sense cicles, coneguda com a α-aciclicitat. Aquesta noció d'aciclicitat és equivalent a la condició de què l'hipergraf sigui conforme (tot clique del graf primari està cobert per alguna hiperaresta) i que el seu graf primari sigui cordal; també és equivalent a la condició de ser reductible al graf buit mitjançant l'algorisme GYO (també conegut com a algorisme de Graham), un procés iteratiu confluent que elimina hiperarestes emprant una definició generalitzada d'orelles. En l'àmbit de la teoria de bases de dades, es coneix que un esquema té certes propietats desitjables si el seu hipergraf subjacent és α-acíclic.

Es pot comprovar en temps lineal si un hipergraf és α-acíclic.

Cal notar que l'α-aciclicitat té la propietat, contrària a la intuïció, de què, si s'afegeixen hiperarestes a un hipergraf α-cíclic, hom pot fer que esdevingui α-acíclic (per exemple, si s'afegeix una hiperaresta que contingui tots els vèrtexs, sempre farà que l'hipergraf esdevingui α-acíclic). Motivat en part per aquest inconvenient, Ronald Fagin definí les nocions de β-aciclicitat i γ-aciclicitat, més fortes que l'anterior. Hom pot establir la β-aciclicitat com el requeriment de què tots els subhipergrafs de l'hipergraf siguin α-acíclics, la qual cosa és equivalent a una definició anterior de Graham. La noció de γ-aciclicitat és una condició més restrictiva, equivalent a diverses propietats desitjables dels esquemes de bases de dades, i relacionada amb els diagrames de Bachman. Tant la β-aciclicitat com la γ-aciclicitat es poden verificar en temps polinòmic.

Aquestes quatre nocions d'aciclicitat són comparables: l'aciclicitat en el sentit de Berge implica la γ-aciclicitat, la qual implica la β-aciclicitat, i aquesta darrera implica la α-aciclicitat. Tanmateix, cap de les implicacions recíproques és certa, de tal manera que aquestes quatre nocions són diferents.

Isomorfisme i igualtat

Un homomorfisme d'hipergrafs és una aplicació del conjunt de vèrtexs d'un hipergraf a un altre, de tal manera que s'envia cada aresta a una altra aresta.

Un hipergraf $H=(X,E)$ és isomorf a un hipergraf $G=(Y,F)$, escrit com $H\simeq G$, si existeixen una bijecció

$\phi :X\to Y$

i una permutació $\pi$ de $I$ tals que

$\phi (e_{i})=f_{\pi (i)}$.

Hom diu llavors que la bijecció $\phi$ és l'isomorfisme entre els grafs. Observem que

$H\simeq G$ si i només si $H^{*}\simeq G^{*}$.

Quan les arestes d'un hipergraf estan etiquetades de forma explícita, hom té la noció addicional d'isomorfisme fort. Hom diu que $H$ és fortament isomorf a $G$ si la permutació és la identitat. Llavors s'escriu $H\cong G$. Cal destacar que tot geaf fortament isomorf és isomorf, però el recíproc no és cert.

Quan els vèrtexs d'un hipergraf estan etiquetats de forma explícita, hom pot considerar les nocions d'equivalència i d'igualtat. Es diu que $H$ és equivalent a $G$, escrit $H\equiv G$, si l'isomorfisme $\phi$ compleix

$\phi (x_{n})=y_{n}$

i

$\phi (e_{i})=f_{\pi (i)}$.

Observem que

$H\equiv G$ si i només si $H^{*}\cong G^{*}$.

Si, a més, la permutació $\pi$ és la identitat, hom diu que $H$ és igual a $G$, i s'escriu $H=G$. Notem que, amb aquesta definició d'igualtat, els grafs són autoduals:

$\left(H^{*}\right)^{*}=H$.

Un automorfisme d'un hipergraf és un isomorfisme d'un conjunt de vèrtexs en ell mateix, de tal manera que és un reetiquetatge dels vèrtexs. El conjunt d'automorfismes d'un hipergraf H (= (X, E)) forma un grup amb la composició, anomenat el grup d'automorfismes, de l'hipergraf, simbolitzat per Aut(H).

Exemples

Considerem l'hipergraf $H$ amb arestes

${\begin{aligned}H=\lbrace &e_{1}=\lbrace a,b\rbrace ,\\&e_{2}=\lbrace b,c\rbrace ,\\&e_{3}=\lbrace c,d\rbrace ,\\&e_{4}=\lbrace d,a\rbrace ,\\&e_{5}=\lbrace b,d\rbrace ,\\&e_{6}=\lbrace a,c\rbrace \rbrace \end{aligned}}$

i

${\begin{aligned}G=\lbrace &f_{1}=\lbrace \alpha ,\beta \rbrace ,\\&f_{2}=\lbrace \beta ,\gamma \rbrace ,\\&f_{3}=\lbrace \gamma ,\delta \rbrace ,\\&f_{4}=\lbrace \delta ,\alpha \rbrace ,\\&f_{5}=\lbrace \alpha ,\gamma \rbrace ,\\&f_{6}=\lbrace \beta ,\delta \rbrace \rbrace \end{aligned}}$

Clarament, $H$ i $G$ són isomorfs (amb $\phi (a)=\alpha$, etc.), però no són fortament isomorfs: per exemple, a $H$, el vèrtex $a$ forma part de les arestes 1, 4 i 6, és a dir,

$e_{1}\cap e_{4}\cap e_{6}=\lbrace a\rbrace$.

Però en el graf $G$, no hi ha cap vèrtex compartit per les arestes 1, 4 i 6:

$f_{1}\cap f_{4}\cap f_{6}=\varnothing$.

En aquest exemple, $H$ i $G$ són equivalents, $H\equiv G$, i els duals són fortament isomorfs: $H^{*}\cong G^{*}$.

Hipergrafs simètrics

El rang $r(H)$ d'un hipergraf $H$ és la màxima cardinalitat d'entre les arestes de l'hipergraf. Si totes les arestes tenen la mateixa cardinalitat k, es diu que l'hipergraf és uniforme o k-uniforme; també es parla d'un k-hipergraf. Un graf és, simplement, un hipergraf 2-uniforme.

El grau d(v) d'un vèrtex v és el nombre d'arestes que el contenen. Hom diu que H és k-regular si tots els vèrtexs tenen grau k.

El dual d'un hipergraf uniforme és regular, i viceversa.

Hom diu que dos vèrtexs x i y són simètrics si existeix un automorfisme tal que $\phi (x)=y$. Hom diu que dues arestes $e_{i}$ i $e_{j}$ són simètriques si existeix un automorfisme tal que $\phi (e_{i})=e_{j}$.

Hom diu que un hipergraf és vèrtex-transitiu (o vèrtex-simètric) si tots els seus vèrtexs són simètrics. Anàlogament, un hipergraf és aresta-transitiu si totes les seves arestes són simètriques. Si un hipergraf és alhora aresta-transitiu i vèrtex-transitiu, llavors hom diu que l'hipergraf és transitiu.

Per les propietats de dualitat dels hipergrafs, l'estudi de l'aresta-transitivitat és idèntic a l'estudi de la vèrtex-transitivitat.

Transversals

La transversal d'un hipergraf H = (X, E) és un conjunt $T\subseteq X$ que té una intersecció no buida amb tota aresta de l'hipergraf. Hom diu que una transversal T és mínima si cap subconjunt propi de T és transversal. L'hipergraf transversal de H és l'hipergraf (X, F) on el conjunt d'arestes F consisteix en totes les transversals mínimes de H.

El càlcul de l'hipergraf transversal té aplicacions en optimització combinatòria, en teoria de jocs, i en diversos camps de les ciències de la computació, com l'aprenentatge automàtic, l'indexat de bases de dades, el problema de satisfactibilitat, la mineria de dades, i l'optimització de codi.

Matriu d'incidència

Siguin $V=\{v_{1},v_{2},~\ldots ,~v_{n}\}$ i $E=\{e_{1},e_{2},~\ldots ~e_{m}\}$. Tot hipergraf té una matriu d'incidència $A=(a_{ij})$ de dimensió $n\times m$ on

$a_{ij}={\begin{cases}1&{\text{si }}v_{i}\in e_{j}\\0&{\text{altrament.}}\end{cases}}$

La transposada $A^{t}$ de la matriu d'incidència defineix un hipergraf $H^{*}=(V^{*},\ E^{*})$, anomenat dual de $H$, on $V^{*}$ és un conjunt de m elements i $E^{*}$ és un conjunt de n elements de subcinjunts de $V^{*}$. Donats $v_{j}^{*}\in V^{*}$ i $e_{i}^{*}\in E^{*}$, es té que $v_{j}^{*}\in e_{i}^{*}$ si i només si $a_{ij}=1$.

Coloració d'hipergrafs

La coloració d'hipergrafs en sentit clàssic és el procés d'assignar un dels colors del conjunt $\{1,2,3,\ldots ,\lambda \}$ a cada vèrtex de l'hipergraf, de tal manera que cada hiperaresta contingui almenys dos vèrtexs de colors diferents. En altres paraules, no hi pot haver cap hiperaresta monocromàtica amb cardinalitat ≥2. En aquest sentit, és una generalització directa de la coloració de grafs. El nombre mínim de diferents colors necessaris per a acolorir un hipergraf s'anomena nombre cromàtic de l'hipergraf.

Hom diu que un hipergraf és k-acolorible si es necessiten un màxim de k colors per acolorir-lo. Els hipergrafs 2-acoloribles són exactament els hipergrafs bipartits.

Existeixen moltes generalitzacions de la coloració clàssica d'hipergrafs. Una d'elles és l'anomenada coloració mixta d'hipergrafs, on es permeten arestes monocromàtiques. Alguns hipergrafs mixtos no són acoloribles amb cap nombre de colors. Quan un hipergraf admet una coloració, llavors els nombres mínim i màxim de colors emprats s'anomenen nombre cromàtic inferior i nombre cromàtic superior, respectivament.

Particions

Un teorema de partició degut a Elayne Dauber afirma que, per a un hipergraf aresta-transitiu $H=(X,E)$, existeix una partició

$(X_{1},X_{2},\cdots ,X_{K})$

del conjunt de vèrtexs $X$ tal que el subhipergraf $H_{X_{k}}$ generat per $X_{k}$ és transitiu per a tot $1\leq k\leq K$, i tal que

$\sum _{k=1}^{K}r\left(H_{X_{k}}\right)=r(H)$

on $r(H)$ és el rang de H.

Com a corol·lari, un hipergraf aresta-transitiu que no sigui vèrtex-transitiu és acolorible amb 2 colors.

Les particions de grafs (i en particular, les particions d'hipergrafs) tenen moltes aplicacions al disseny de circuits integrats i computació paral·lela. Els algorismes de partició d'hipergrafs Eficient i Escalable també són importants per al processament d'hipergrafs de gran escala en tasques d'aprenentatge automàtic.

Teoremes

Molts teoremes i conceptes sobre grafs també són vàlids per a hipergrafs. El teorema de Ramsey i el Graf línia d'un hipergraf en són dos exemples típics. Alguns mètodes per a l'estudi de les simetries dels grafs apliquen també al cas d'hipergrafs.

Dos teoremes destacats són el teorema d'Erdős–Ko–Rado i el teorema de Kruskal–Katona sobre hipergrafs uniformes.

Representació gràfica d'hipergrafs

Aquest diagrama electrònic es pot interpretar com la representació gràfica d'un hipergraf on quatre vèrtexs (simbolitzats pels rectangles i cercles blancs) estan connectats per tres hiperarestes.

Tot i que els hipergrafs són més difícils de dibuixar en paper que els grafs, diversos investigadors han estudiat mètodes per a la visualització d'hipergrafs.

Una possible representació visual per a hipergrafs, semblant a la representació gràfica habitual per a grafs, on les corbes del pla en representen les arestes, estableix que els vèrtexs d'un hipergraf es representin mitjançant punts, cercles o caixes, i les seves arestes es dibuixin com arbres que tenen els vèrtexs com a fulles. Si els vèrtexs es representen mitjançant punts, les hiperarestes també es poden mostrar com a corbes suaus que connecten conjunts de punts, o com a corbes tancades simples que encerclen conjunts de punts.

Un diagrama de Venn d'ordre 4, que es pot interpretar com una subrepresentació gràfica d'un hipergraf amb 15 vèrtexs (les 15 regions acolorides) i 4 hiperarestes (les 4 el·lipses).

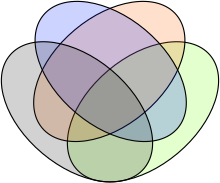
En un altre estil de visualització d'hipergrafs, el model de subdivisions, hom subdivideix el pla en regions, on cada regió representa un sol vèrtex de l'hipergraf. Les hiperarestes de l'hipergraf s'interpreten com a subconjunts contigus d'aquestes regions, simbolitzats per colors, dibuixant-ne la frontera exterior, o una combinació d'ambdues. Un diagrama de Venn d'ordre n, per exemple, es pot veure com una representació gràfica de les subdivisions d'un hipergraf amb n hiperarestes (les corbes que defineixen el diagrama) i 2ⁿ − 1 vèrtexs (representats per les regions resultants de les subdivisions del pla provocades per les corbes). En contrast amb els grafs planars, el problema de determinar si un hipergraf admet una representació gràfica planar en subdivisions és NP-complet, però es pot comprovar l'existència d'una representació gràfica d'aquest tipus de manera eficient quan el patró d'adjacència de les regions està restringit a un camí, un cicle o un arbre.

Generalitzacions

Una possible generalització d'un hipergraf consisteix a permetre que les arestes apuntin a d'altres arestes. Existeixen dues variacions d'aquesta generalització. En la primera, les arestes consisteixen no només d'un subconjunt de vèrtexs, sinó que també poden contenir subconjunts de vèrtexs, ad infinitum. Essencialment, tota aresta és simplement un node intern d'un arbre o graf acíclic dirigit, i els vèrtexs són els nodes extrems. Un hipergraf és llavors una col·lecció d'arbres amb uns vèrtexs compartits (és a dir, un vèrtex donat pot aparèixer en diversos arbres diferents). Recíprocament, qualsevol col·lecció d'arbres es pot interpretar com un hipergraf amb aquesta generalització. Com que els arbres s'utilitzen freqüentment en molts àmbits de les ciències de la computació i en altres branques de les matemàtiques, es pot afirmar que els hipergrafs també hi apareixen. Per exemple, aquesta generalització sorgeix de manera natural com a model de l'àlgebra de termes; les arestes corresponen als termes i els vèrtexs corresponen a les constants o variables.

Per a un hipergraf d'aquest tipus, la pertinença a un conjunt proporciona un ordre, però no és ni un ordre parcial ni un preordre, ja que no és transitiu. El graf corresponent al graf de Levi d'aquesta generalització és un graf acíclic dirigit. Considerem, per exemple, l'hipergraf generalitzat que té per vèrtexs el conjunt $V=\{a,b\}$ i amb arestes $e_{1}=\{a,b\}$ i $e_{2}=\{a,e_{1}\}$. Llavors, encara que $b\in e_{1}$ i $e_{1}\in e_{2}$, no és cert que $b\in e_{2}$. Tanmateix, la clausura transitiva de la pertinença a conjunts per a aquests hipergrafs sí que indueix un ordre parcial, i "aplana" l'hipergraf en un conjunt parcialment ordenat.

Per altra banda, es pot permetre que les arestes apuntin a altres arestes (independentment del requeriment de què les arestes estiguin ordenades com a grafs acíclics dirigits). Això permet construir grafs amb bucles d'arestes, que no tenen per què contenir vèrtexs. Per exemple, considerem l'hipergraf generalitzat de dues arestes $e_{1}$ i $e_{2}$, i zero vèrtexs, de tal manera que $e_{1}=\{e_{2}\}$ i $e_{2}=\{e_{1}\}$. Com que aquest bucle és infinitament recursiu, els conjunts de les arestes trenquen l'axioma de fundació. En particular, no hi ha cap clausura transitiva de la pertinença a conjunts per a aquests hipergrafs. Encara que aquestes estructures puguin semblar estranyes inicialment, es pot interpretar com que la generalització equivalent del seu graf de Levi ja no és bipartit, sinó un graf dirigit en general.

La matriu d'incidència generalitzada per a aquests hipergrafs és, per definició, una matriu quadrada, amb un rang igual a la suma del nombre de vèrtexs i el nombre d'arestes. Així, en l'exemple anterior, la matriu d'incidència és simplement

${\begin{pmatrix}0&1\\1&0\end{pmatrix}}.$

Aprenentatge d'hipergrafs

Els hipergrafs s'han emprat freqüentment en tasques d'aprenentatge automàtic com a model de dades. Entre les seves aplicacions destaquen els sistemes de recomanació (on les hiperarestes representen les comunitats), la recuperació d'imatges (on les hiperarestes representen les correlacions), i la bioinformàtica (on les hiperarestes representen les interaccions bioquímiques). Les tècniques d'aprenentatge d'hipergrafs representatius inclouen l'agrupament espectral d'hipergrafs, que amplia la teoria espectral de grafs amb el laplacià per a hipergrafs, i l'aprenentatge semisupervisat d'hipergrafs, que introdueix costos estructurals addicionals a l'hipergraf per dirigir els resultats de l'aprenentatge. Per a hipergrafs a gran escala, també està disponible un entorn de treball distribuït construït amb Apache Spark.

Bibliografia

• Berge, Claude. Hypergraphs: Combinatorics of finite sets. North-Holland, 1989. ISBN 978-0444874894. 
• Berge, Claude; Ray-Chaudhuri, Dijen. Hypergraph Seminar, Ohio State University 1972. 411. Springer-Verlag, 2009 (Lecture Notes in Mathematics). ISBN 978-3540068464. 
• Michiel Hazewinkel (ed.). Hypergraph. Encyclopedia of Mathematics (en anglès). Springer, 2001. ISBN 978-1-55608-010-4. 
• Bretto, Alain. Hypergraph Theory: an Introduction. Springer, 2013. ISBN 978-3-319-03370-9. 
• Voloshin, Vitaly I. Coloring Mixed Hypergraphs: Theory, Algorithms and Applications. American Mathematical Society, 2002 (Fields Institute Monographs). ISBN 978-0-8218-2812-0. 
• Voloshin, Vitaly I. Introduction to Graph and Hypergraph Theory. Nova Science Publishers, Inc., 2009. ISBN 978-1-60692-372-6. 

Aquest article incorpora material de l'article hypergraph Arxivat 2016-05-14 a Wayback Machine. a PlanetMath, llicenciat sota la Llicència Creative Commons Reconeixement-Compartir Igual.

Vegeu també

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Hipergraf

• Matroide
• Multigraf