Segon principi de la termodinàmica
|
|
L'article necessita algunes millores en la redacció de la introducció. |
| Lleis de la termodinàmica |
|---|
 |
| 0. Llei zero de la termodinàmica |
| 1. Primera llei de la termodinàmica |
| 2. Segona llei de la termodinàmica |
| 3. Tercera llei de la termodinàmica |
El segon principi de la termodinàmica diu que l'entropia d’un sistema aïllat augmenta quan es realitza un procés espontani irreversible, , o roman constant si és reversible, .[1]
Per tant, els processos termodinàmicament irreversibles, com el refredament d’un cos fins a la temperatura del medi o l'expansió lliure dels gasos, són processos espontanis que han d’anar acompanyats sempre d’un increment de l'entropia , magnitud extensiva que mesura el desordre d'un sistema. Tanmateix els sistemes habituals no estan aïllats i poden, per tant, intercanviar calor, treball i matèria amb l'entorn o medi. En aquest cas, podem considerar que el sistema més els voltants formen un sistema aïllat, per la qual cosa , on representa l'entropia total del sistema i el medi que l'envolta. En qualsevol cas, l'univers és un sistema aïllat, i per això sempre es compleix que en un procés espontani .[2]
En els sistemes no aïllats els processos espontanis es produeixen fins que el sistema arriba a un estat d’equilibri, en el que es manté constant. És a dir, mentre el sistema evoluciona espontàniament l'entropia augmenta, i l'equilibri es dona quan la suma és màxima.[2]
Basant-se en la física estadística i en el càlcul de probabilitats, el físic alemany Ludwig Boltzmann demostrà que el pas de calor d’un cos calent a un cos fred era el més probable, però que el cas invers no era pas impossible i vendria acompanyat d'una disminució d'entropia. Així, el segon principi deixava de tenir un caràcter absolut i esdevenia estadístic. És a dir que, a causa de les fluctuacions en la distribució molecular, l'entropia d’un sistema aïllat pot disminuir, si bé la probabilitat d’aquest fet és tant més petita com més gran és el de creixement expectat. Recents descobriments han confirmat que a l’Univers es produeixen fenòmens de concentració d’energia (formació de nous estels) que són contraris al segon principi de la termodinàmica.[1]
Entropia
[modifica]
L'entropia és una magnitud extensiva que representa una mesura del desordre del sistema. El desordre d'un sistema ve donat pel nombre de microestats o complexions possibles del sistema. Les molècules d'un sòlid tenen pocs microestats perquè els sòlids són sistemes molt ordenats on les molècules ocupen posicions fixes dins de l'espai i només presenten un moviment de vibració entorn de la posició que ocupen. Per altra banda un gas és un sistema molt desordenat, ja que les molècules es mouen per tot el volum a grans velocitats, xocant contra les parets del recipient i entre elles. El nombre de microestats s'anomena probabilitat termodinàmica i es representa amb la lletra grega omega majúscula .[2]
La probabilitat termodinàmica es relaciona amb l'entropia mitjançant a fórmula de Boltzmann deguda al físic austríac Ludwing Boltzmann (1844–1906):
on és l'anomenada constant de Boltzmann, que té un valor d'1,380 649 × 10–23 J K–1.[3]
Enunciats alternatius
[modifica]Des de l'establiment del segon principi de la termodinàmica varis autors han establert diferents enunciats que són equivalents. Es poden diferenciar dos grups, els preentròpics i els postentròpics, això és, els establerts abans de la definició d'entropia i els establerts posteriorment. Els preentròpics són:
- Enunciat de Kelvin-Planck: És impossible un procés que tengui com únic resultat l'absorció de calor procedent d'un termostat i la seva conversió en treball.
- Enunciat de Clausius: És impossible un procés que tengui com a únic resultat la transferència de calor d'un cos fred a un de calent.
- Teorema de Carnot: El rendiment d'un motor tèrmic és menor o igual al rendiment d'un motor tèrmic de Carnot que treballi entre les mateixes temperatures, i aquest és sempre menor que u.
- Enunciat de Carathéodory: En les proximitats de tot estat d'equilibri hi ha estats d'equilibri inaccessibles adiabàticament des d'ell.[4]
Els enunciats postentròpics són:
- Enunciat entròpic clàssic: En els processos termodinàmics es compleix que , essent igual quan el procés és en equilibri.
- Potencial entropia: De tots els estats caracteritzats pel mateixos valors de l'energia interna i les propietats aditives del sistema associades als diferents tipus de treball, l'entropia assoleix el valor màxim a l'estat d'equilibri.
- Llei de l'increment d'entropia: En un sistema aïllat l'entropia no pot disminuir.[4]
Història
[modifica]
Sadi Carnot
[modifica]A principis del segle xix hi havia una lluita constant per millorar l'eficàcia i la versatilitat de les màquines de vapor, i el 1824 l'oficial d'artilleria Sadi Carnot (1796–1832), publicà l'obra Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance[5] (Reflexions sobre la potència motriu del foc i sobre les màquines dissenyades per a desenvolupar aquesta potència) obrint el camí per a establir les bases de la termodinàmica. Carnot s'havia format a l'École polytechnique de París d'on el seu pare, Lazare Carnot (1753–1823), era un dels seus fundadors i alhora un prestigiós científic i matemàtic de l'època. L'obra de Carnot és una reflexió teòrica i encara que en ella es duen a terme diversos càlculs i determinacions basades en algunes dades experimentals, està consolidada a esbrinar, des d'un punt de vista conceptual, quins són els principis elementals que fan que una màquina tèrmica funcioni, una circumstància que segons Carnot no havia estat plantejada amb la generalitat suficient. Així doncs, els seus resultats hauran de ser aplicables a qualsevol dispositiu independentment de la forma en què estigui dissenyat i dels materials amb què estigui construït.[6]
La novetat en el raonament de Carnot és que per a produir un efecte mecànic a partir de la calor no sols és necessari un cos calent, en aquest cas el fogó de la màquina, sinó també un cos fred cap al qual és transportat el «calòric», sent aquest transport el mecanisme essencial de la producció de treball. Carnot fa veure així mateix que el vapor no és l'única substància que pot ser utilitzada per a produir treball, sinó que l'alternança de calor i fred en una vareta metàl·lica, un líquid, un gas permanent o un vapor d'una altra substància produeix canvis de volum que, almenys en teoria, també poden ser utilitzats per a produir un efecte mecànic aprofitable.[6]
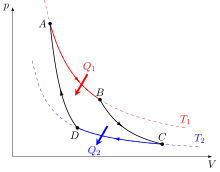
No obstant això, una vegada resolta aquesta qüestió Carnot es planteja si la potència motriu de la calor depèn de la substància emprada o és la mateixa per a totes elles. Per a donar resposta a aquesta pregunta, argumenta que el màxim de potència motriu que s'obté emprant el vapor és també el màxim que s'obté per qualsevol altre procediment, ja que el mateix (màxim rendiment en el nostre llenguatge actual) s'obtindrà quan no es faci cap canvi de temperatura que no sigui aprofitat per a produir un canvi de volum, és a dir que no passi directament calor d'un cos calent a un cos fred sense tenir lloc un altre efecte, o des d'un punt de vista més pràctic, que no hi hagi contacte entre cossos de temperatures sensiblement diferents, amb el que acaba justificant la sensible millora introduïda per James Watt (1736–1819) incorporant el condensador en la màquina de vapor. És a dir la seva conclusió fou que una màquina tèrmica seria més eficient quan per una banda, els intercanvis de calor es realitzassin sempre entre cossos a temperatures molt properes (idealment a la mateixa), minimitzant així el flux irreversible de calor que no produeix treball i quan per l'altra, els processos siguin el menys irreversibles possible. Amb aquestes idees al cap, dissenyà una màquina tèrmica ideal de gran importància, la màquina de Carnot, que funciona segons l'anomenat cicle de Carnot. En aquest cicle termodinàmic, una substància de treball (per exemple un gas ideal) és un sistema que pateix les transformacions següents de forma reversible i cíclica: AB expansió isoterma reversible a la temperatura , BC expansió adiabàtica reversible, CD compressió isoterma a la temperatura i DA compressió adiabàtica reversible.[6]
Inicialment l'obra de Carnot no tingué massa difusió ni influència entre els seus contemporanis; però, un enginyer francès, Émile Clapeyron (1799–1864), en descobrí la transcendència dels resultats de Carnot i de la validesa del seu mètode de raonament i realitzà una revisió de la mateixa que publicà el 1834 en la seva Mémoire sur la puissance motrice de la chaleur (Memòria sobre la potència motriu de la calor).[7] En ella, Clapeyron clarificà i sistematitzà el treball de Carnot. Dibuixà i explicà clarament el procés utilitzat per aquest per a la seva deducció sobre el rendiment màxim, i matematitzà alguns seus resultats fent-los més llegibles per a la comunitat científica de l'època.[6]

William Thomson, Lord Kelvin
[modifica]El físic irlandès William Thomson, posteriorment Lord Kelvin, (1824–1907) observà que l'afirmació bàsica implícita en la teoria de Carnot, que en l'operació d'una màquina una certa quantitat de calor és transferida íntegrament d'un cos de major temperatura a un altre de menor temperatura, entrava en contradicció amb les observacions fetes per James Prescott Joule (1818–1889) que la calor i el treball mecànic són interconvertibles entre si. Aquesta aparent contradicció fou resolta l'any 1850 pel físic alemany Rudolf Clausius (1822–1888) en el seu article Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus fuer die Wärmelehre selbst ableiten lassen[8] (Sobre la força motriu de la calor i sobre les lleis deduïbles d'aquesta concernents a la naturalesa de la mateixa). Clausius considerà que si hom suposa que no tota la calor passa del focus calent al focus fred sinó que una part d'ell mateix apareix en la forma d'efecte mecànic (treball), els raonaments de Carnot i els de Joule són perfectament compatibles. Tot i que Clausius considerà errònia la idea de Carnot que la calor és transferit íntegrament del cos calent al fred, això no invalidava la resta del seu raonament, en particular el fet que la màquina que hauria de proporcionar màxim rendiment és aquella que si es fa operar en sentit contrari tant la mateixa com els voltants recuperen l'estat que posseïen inicialment i en la qual no hi ha dues parts a diferent temperatura que entrin en contacte directe.[6]
Entre 1851 i 1853 Thomson, publicà una sèrie de treballs amb el títol genèric On the dynamical theory of heat...[9] (Sobre la teoria dinàmica de la calor...) en els quals acceptà la solució de Clausius, i aprofundí en el tema amb les seves pròpies conclusions i raonaments. Establí el que anomenà Principis fonamentals de la teoria de la potència motriu de la calor en la forma de dues proposicions, la primera de les quals atribueix a Joule i la segona a Carnot i a Clausius:
- Proposició I. Quan iguals quantitats d'efecte mecànic són produïdes pel mitjà que sigui de fonts purament tèrmiques o perdudes en efectes purament tèrmics, desapareixen o es generen iguals quantitats de calor.
- Proposició II. Si una màquina és tal que quan funciona en sentit invers, els agents físics i mecànics en qualsevol part dels seus moviments són invertits, aquesta produeix d'una mateixa quantitat de calor, tant efecte mecànic com el que pugui produir-se per qualsevol màquina termodinàmica amb les mateixes temperatures calenta i freda.[6]

Rudolf Clausius
[modifica]No obstant això el pas més avançat el tornaria a donar Clausius el 1854, en un treball publicat amb el títol Ueber eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie[10] (Sobre una forma modificada de la segona llei de la teoria mecànica de la calor), on ja en el mateix títol reconeix que la teoria que considera la calor com un estat de moviment, o teoria mecànica de la calor, pot ser basada en dos principis o teoremes elementals:
- Primer teorema: El treball mecànic es pot transformar en calor i recíprocament la calor en treball mecànic, sent la magnitud d'un sempre proporcional a la de l'altre.
- Segon teorema: La calor mai passa d'un cos fred a un altre més calent sense que un altre canvi relacionat amb això tingui lloc al mateix temps.[6]
El 1862, en l'article Ueber die Anwendung des Satzes von der Aequivalenz der Verwandlungen auf die innere Arbeit[11] (Sobre l’aplicació del principi d’equivalència de les transformacions del treball intern) presentà el conegut teorema o desigualtat de Clausius, que diu que per a tot procés cíclic es compleix que:
Essent calor que entra al sistema i la temperatura del punt d'entrada. La integra cíclica és igual a zero quan el cicle termodinàmic és reversible, i menor que zero quan és irreversible.[12]
No obstant això, el pas decisiu pel que fa a aquesta magnitud el dona a l'article publicat el 1865 sota el títol Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie[13] (Sobre les diferents formes de les equacions fonamentals de la teoria mecànica de la calor), on defineix l'entropia com:[12]
Referències
[modifica]- ↑ 1,0 1,1 «Segon principi de la termodinàmica». Gran Enciclopèdia Catalana. Barcelona: Grup Enciclopèdia Catalana.
- ↑ 2,0 2,1 2,2 Díaz Peña, M.; Roig Muntaner, A. Química física. Madrid: Alhambra, 1972 (impresión de 1989). ISBN 84-205-0569-2.
- ↑ «CODATA Value: Boltzmann constant». [Consulta: 30 maig 2021].
- ↑ 4,0 4,1 Garrido Garrido, Julián «Formulaciones del segundo principio de la termodinámica». Crítica (México D. F. En línea), 19, 56, 10-12-1987, pàg. 77–110. DOI: 10.22201/iifs.18704905e.1987.647. ISSN: 1870-4905.
- ↑ Carnot, Sadi. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. París: Bachelier, 1824.
- ↑ 6,0 6,1 6,2 6,3 6,4 6,5 6,6 Pérez Cruz, J. «La Termodinámica de Carnot a Clausius». La Ciencia antes de la Gran Guerra. Encuentros Educativos Actas año XVII., 2009.
- ↑ Clapeyron, É. Mémoire sur la puissance motrice de la chaleur (en francès). Éditions Jacques Gabay, 1834.
- ↑ Clausius, R. «Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen». Annalen der Physik und Chemie, 155, 3, 1850, pàg. 368–397. DOI: 10.1002/andp.18501550306. ISSN: 0003-3804.
- ↑ Thomson, William «XV.— On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule's Equivalent of a Thermal Unit, and M. Regnault's Observations on Steam» (en anglès). Transactions of the Royal Society of Edinburgh, 20, 2, 1853, pàg. 261–288. DOI: 10.1017/S0080456800033172. ISSN: 0080-4568.
- ↑ Clausius, R. «Ueber eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie» (en anglès). Annalen der Physik, 169, 12, 1854, pàg. 481–506. DOI: 10.1002/andp.18541691202. ISSN: 1521-3889.
- ↑ Clausius, R. «Ueber die Anwendung des Satzes von der Aequivalenz der Verwandlungen auf die innere Arbeit» (en anglès). Annalen der Physik, 192, 5, 1862, pàg. 73–112. DOI: 10.1002/andp.18621920506. ISSN: 1521-3889.
- ↑ 12,0 12,1 Rodríguez Renuncio, Juan Antonio. Termodinámica química. 2a. ed. Madrid: Síntesis, 2000. ISBN 84-7738-581-5.
- ↑ Clausius, R. «Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie» (en anglès). Annalen der Physik, 201, 7, 1865, pàg. 353–400. DOI: 10.1002/andp.18652010702. ISSN: 1521-3889.


















