Triangle de Penrose

El triangle de Penrose és un objecte impossible que va ser creat el 1934 per l'artista suec Oscar Reutersvärd. Posteriorment, va ser redescobert de manera independent pel físic Roger Penrose, en la dècada de 1950, que el va fer popular, descrivint-lo com a "impossibilitat en la seva més pura forma".[1] Apareix de manera destacada en les obres de l'artista M. C. Escher, fins al punt que va ser parcialment inspirat per les seves primeres imatges d'objectes impossibles. El terme pot referir-se tant a l'objecte impossible com a la seva representació bidimensional.
Aquest objecte impossible aparenta ser un objecte sòlid, format per tres trams rectes de secció quadrada, que es troben units formant angle recte en els extrems del triangle que conformen. Aquesta combinació de propietats no pot ser satisfeta per cap figura tridimensional en un espai euclidià ordinari. En canvi, en certes 3-varietats sí que poden existir.[2]
Existeixen, a més, objectes tridimensionals sòlids que, quan són observats des de l'angle apropiat, aparenten ser triangles de Penrose.

La litografia de M. C. Escher Waterfall representa un corrent d'aigua que flueix en ziga-zaga a través dels costats de dos triangles de Penrose allargats, de manera que acaba dos pisos més amunt d'on comença. La cascada resultant, formada en els costats curts dels dos triangles, fa funcionar una sínia. Escher puntualitza, amb humor, que per poder mantenir la sínia en funcionament, és necessari afegir una mica d'aigua de tant en tant, per compensar les pèrdues per evaporació.
Si es traça una cinta recorrent el triangle de Penrose, es forma una banda de Möbius de 3 voltes.
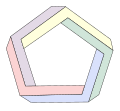
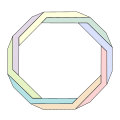
Altres polígons de Penrose[modifica]
La construcció d'un triangle de Penrose es pot generalitzar amb la resta de polígons regulars, creant així un polígon de Penrose. Tanmateix, l'efecte visual no és tan impactant, ja que en incrementar el nombre de costats la imatge esdevé més complexa i és més difícil de concebre.
Referències[modifica]
- ↑ J. Robinson (1998), The Psychology of Visual Illusion, Dover, Nova York. ISBN 0-486-40449-8.
- ↑ Francis, George. A topological picturebook. Springer, 1988. ISBN 0387964266. Al capítol del triangle de Penrose, Francis atribueix aquesta observació a John Stillwell.
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Triangle de Penrose |
- A family of impossible figures studied by knot theory Arxivat 2007-11-17 a Wayback Machine. (anglès).
- Escher for Real constructions Arxivat 2008-01-20 a Wayback Machine. (anglès).