Usuari:Meldor/Joc de la vida
|
|

El joc de la vida és un autòmata cel·lular dissenyat pel matemàtic britànic John Horton Conway el 1970.
De fet, el joc és un joc de zero jugadors, és a dir, la seva evolució queda determinada tan sols pel seu estat inicial, sense que es necessiti cap mena d'interacció amb jugadors humans. La forma de jugar al joc de la vida és mitjançant la configuració del seu estat inicial, i observant com evoluciona. Existeix una variant on dos jugadors competeixen entre ells.
Regles[modifica]
L'univers del joc de la vida és una malla ortogonal bidimensional infinita, de cel·les individuals, cadascuna de les quals té dos estats possibles: viu o mort. Cada cel·la interacciona amb els seus vuit veïns, que són les cel·les a què està connectada horitzontalment, verticalment o diagonalment. A cada unitat de temps, es donen les següents transicions:
- Tota cel·la viva amb menys de dos veïns vius mor (de solitut).
- Tota cel·la viva amb més de tres veïns vius mor (de sobreconcentració).
- Tota cel·la viva amb dos o tres veïns vius, segueix viva per a la següent generació.
- Tota cel·la morta amb exactament tres veïns vius torna a la vida.
Aquest patró inicial constitueix la llavor del sistema. La primera generació és creada aplicant aquestes regles simultàniament a totes les cel·les de la malla. Les regles es continuen aplicant repetidament per crear futures generacions.
Origen[modifica]
Conway estava interessant en un problema presentat els anys 40 pel matemàtic John von Neumann, que intentava trobar una màquina hipotètica que pogués construir còpies d'ella mateixa. Va aconseguir trobar un model matemàtic amb regles molt complexes sobre una malla amb coordenades cartesianes. Conway va intentar simplicar les idees de Von Neumann, i de fet ho va aconseguir. Unint el seu èxit en el problema de Leech de teoria de grups amb el seu interès en les idees de Von Neumann, Conway va donar llum al Joc de la vida.
Va aparèixer per primer cop a l'octubre de 1970, en un article del Scientific American, a la columna de Martin Gardner de Jocs matemàtics. Des d'un punt de vista teòric, el joc resulta molt interessant, perquè té la capacitat d'una Màquina de Turing universal; és a dir, tot el que pot ser computat algorísmicament pot ser computat amb un joc de la vida. Gardner va escriure: {{cquote|El joc va fer famós a l'instant Conway, però també va obrir una nova branca en la investigació matemàtica, el camp dels autòmates cel·lulars (...) Per l'analogia del joc de la vida amb el naixement, caiguda i alteracions de la societat amb els organismes vius, pertany a una classe emergent del que s'anomenen jocs de simulació (jocs que s'assemblen a processos de la vida real).
Des de la seva publicació, ha atret molt d'interès per les maneres sorprenents com poden evolucionar els patrons. El joc de la vida és un exemple d'auto-organització. Resulta interessant per a moltes branques de la ciència, incloent la física, la biologia, l'economia, les matemàtiques o la filosofia, i d'altres ciències que observen la manera en què regles molt senzilles poden generar patrons complexos.
Segurament va ajudar a la seva popularitat el fet que el joc de la vida sorgís coincidint amb l'aparició d'una nova generació d'ordenadors barats, fet que possibilitava que el joc podia desenvolupar-se durant hores en aquestes màquines, que d'altra manera quedaven sense utilitzar durant la nit. Pel que fa a aquest aspecte, la seva popularitat va ser molt superior a la que despertaria més endavant la generació per ordenador de fractals. Per a molts aficionats, el joc de la vida era simplement un repte de programació, una manera de malgastar cicles de CPU. Per altres, el joc tenia més connotacions filosòfiques. Va esdevenir objecte de culte en els anys 70 i més endavant; desenvolupament actuals han arribat a crear emulacions teòriques de sistemes d'ordenador en els límits d'un taulell del joc de la vida.
Conway va escollir les regles amb cura, després de molta experimentació, per complir tres criteris:
- No hi hauria d'haver un patró inicial pel que existeixi una prova simple que la població pot créixer indefinidament.
- Hi hauria d'haver patrons inicials que aparentment creixin sense límit.
- Hi hauria d'haver patrons inicials simples que creixin i canviïn per un període considerable de temps abans de finalitzar de les següents maneres possibles:
- Esvaïnt-se completament (per sobreconcentració o per arribar a dispersar-se en excés).
- Entrant en una configuració estable que romangui sense canvis, o entrant en una fase oscil·latòria en què es repeteix un cicle sense fi de dos o més períodes.
Exemples de patrons[modifica]

Hi ha molts tipus diferents de patrons en el joc de la vida, incloent patrons estàtics, patrons que es repeteixen o oscil·latoris, i patrons que es mouen al llarg de la malla (naus). Els exemples més simples de cadascuna de les tres classes es mostren abaix, amb el conveni habitual de mostrar les cel·les vives en negre i les mortes en blanc.
| |
|
|
|
|
 |
| Bloc | Barca | Pampallugador | Gripau | Planejador | Nau lleugera |
| Block | Boat | Blinker | Toad | Glider | LWSS |
El "bloc" i la "barca" són patrons estàtics vius, el "pampallugador" i el "gripau" són oscil·ladors, i el "planejador" i la "nau lleugera" són naus.
Els patrons anomenats "Matusalems" (Methuselah) poden evolucionar durant llargs períodes abans de repetir-se. "Diehard" és un patró que desapareix després de 130 passos, mentre que "Acorn" triga 5206 generacions en estabilitzar-se, i en aquest temps genera 25 planejadors.
| |
|
| Diehard | Acorn |
Al principi, Conway va conjecturar que cap patró podia créixer indefinidament, és a dir, que per cada configuració inicial de cel·les vives, la població no podia créixer per sobre d'una determinada cota superior. En la primera presentació del joc, a Mathematical Games, Conway va oferir un premi de 50$ per a la primera persona que pogués demostrar la certesa o falsetat de la conjectura abans de finals de 1970. Una manera de demostrar que la conjectura era falsa seria descobrint patrons que contínuament afegeixen comptadors a la malla: una "pistola", que seria una configuració que dispara repetidament objectes com el "planejador", o el "tren", una configuració que es mogués deixant darrera una marca de "fum".
El premi va ser guanyat el novembre d'aquell mateix any per un equip del Massachusetts Institute of Technology, liderat per Bill Gosper; la "pistola de Gosper" (Gosper Gun), mostrada a sota, produeix el primer planejador en la 15ena generació, i un altre planejador cada 30 generacions. Aquesta primera pistola de planejadors és encara la més petita coneguda avui en dia.
Més tard, es van trobar patrons més simples que també creixien indefinidament. Els tres patrons següents ho fan: els dos primers creen un mecanisme de blocs, i el tercer en crea dos. El primer només té 10 cel·les vives (s'ha demostrat que és la mínima quantitat necessària). La segona cap en una malla de 5x5. La tercera només té una cel·la d'alçada.
  |
Later discoveries included other "guns", which are stationary and shoot out gliders or other spaceships; "puffers", which move along leaving behind a trail of debris; and "rakes", which move and emit spaceships. Gosper also constructed the first pattern with an asymptotically optimal quadratic growth rate, called a "breeder", which worked by leaving behind a trail of guns.
It is possible for gliders to interact with other objects in interesting ways. For example, if two gliders are shot at a block in just the right way, the block will move closer to the source of the gliders. If three gliders are shot in just the right way, the block will move farther away. This "sliding block memory" can be used to simulate a counter. It is possible to construct logic gates such as AND, OR and NOT using gliders. It is possible to build a pattern which acts like a finite state machine connected to two counters. This has the same computational power as a universal Turing machine, so the Game of Life is as powerful as any computer with unlimited memory: it is Turing complete.
Furthermore, a pattern can contain a collection of guns that combine to construct new objects, including copies of the original pattern. A "universal constructor" can be built which contains a Turing complete computer, and which can build many types of complex objects, including more copies of itself. Descriptions of these constructions are given in Winning Ways by Conway, Elwyn Berlekamp and Richard Guy.
Iteration[modifica]
From a random initial pattern of living cells on the grid, observers will find the population constantly changing as the generations tick by. The patterns that emerge from the simple rules may be considered a form of beauty. Small isolated subpatterns with no initial symmetry tend to become symmetrical. Once this happens the symmetry may increase in richness, but it cannot be lost unless a nearby subpattern comes close enough to disturb it. In a very few cases the society eventually dies out, with all living cells vanishing, though this may not happen for a great many generations. Most initial patterns eventually "burn out", producing either stable figures or patterns that oscillate forever between two or more states; many also produce one or more gliders or spaceships that travel indefinitely away from the initial location.
Algorithms[modifica]
The earliest results in the Game of Life were obtained without the use of computers. The simplest still-lifes and oscillators were discovered while tracking the fates of various small starting configurations using graph paper, blackboards, physical game boards, for instance Go, and the like. During this early research, Conway discovered that the F-pentomino (which he called the "R-pentomino") failed to stabilise in a small number of generations.
These discoveries inspired computer programmers over the world to write programs to track the evolution of Life patterns. Most of the early algorithms were similar. They represented Life patterns as two-dimensional arrays in computer memory. Typically two arrays are used, one to hold the current generation and one in which to calculate its successor. Often 0 and 1 represent dead and live cells, respectively. A double loop considers each element of the current array in turn, counting the live neighbours of each cell to decide whether the corresponding element of the successor array should be 0 or 1. The successor array is displayed. For the next iteration the arrays swap roles so that the successor array in the last iteration becomes the current array in the next iteration.
A variety of minor enhancements to this basic scheme are possible, and there are many ways to save unnecessary computation. A cell that did not change at the last time step, and none of whose neighbours changed, is guaranteed not to change at the current time step as well, so a program that keeps track of which areas are active can save time by not updating the inactive zones.
In principle, the Life field is infinite, but computers have finite memory, and usually array sizes must be declared in advance. This leads to problems when the active area encroaches on the border of the array. Programmers have used several strategies to address these problems. The simplest strategy is simply to assume that every cell outside the array is dead. This is easy to program, but leads to inaccurate results when the active area crosses the boundary. A more sophisticated trick is to consider the left and right edges of the field to be stitched together, and the top and bottom edges also, yielding a toroidal array. The result is that active areas that move across a field edge reappear at the opposite edge. Inaccuracy can still result if the pattern grows too large, but at least there are no pathological edge effects. Techniques of dynamic storage allocation may also be used, creating ever-larger arrays to hold growing patterns.
Alternatively, the programmer may abandon the notion of representing the Life field with a 2-dimensional array, and use a different data structure, like a vector of coordinate pairs representing live cells. This approach allows the pattern to move about the field unhindered, as long as the population does not exceed the size of the live-coordinate array. The drawback is that counting live neighbours becomes a search operation, slowing down simulation speed. With more sophisticated data structures this problem can also be largely solved.
For exploring large patterns at great time depths, sophisticated algorithms like Hashlife may be useful.
Variations on Life[modifica]
Since Life's original inception, new rules have been developed. The standard Game of Life, in which a cell is "born" if it has exactly 3 neighbours, stays alive if it has 2 or 3 living neighbours, and dies otherwise, is symbolised as "23/3". The first number, or list of numbers, is what is required for a cell to continue. The second set is the requirement for birth. Hence "16/6" means "a cell is born if there are 6 neighbours, and lives on if there are either 1 or 6 neighbours". HighLife is therefore 23/36, because having 6 neighbours, in addition to the original game's 23/3 rule, causes a birth. HighLife is best known for its replicators. Additional variations on Life exist, although the vast majority of these universes are either too chaotic or desolate.

Some variations modify the geometry of the universe as well as the rule. The above variations can be thought of as 2D Square, because the world is two-dimensional and laid out in a square grid. 3D Square and 1D Square variations have been developed, as have 2D Hexagonal variations where the grid is hexagonal or triangular instead of square.
Conway's rules may also be generalized so that instead of two states (live and dead) there are three or more. State transitions are then determined either by a weighting system or by a table specifying separate transition rules for each state; for example, Mirek's Cellebration's multi-coloured "Rules Table" and "Weighted Life" rule families each include sample rules equivalent to Conway's Life.
Patterns relating to fractals and fractal systems may also be observed in certain Life-like variations. For example, the automaton 12/1 generates four very close approximations to the Sierpinski Triangle when applied to a single live cell.
Immigration is a variation that is the same as the Game of Life, except that there are two ON states (often expressed as two different colors). Whenever a new cell is born, it takes on the ON state that is the majority in the three cells that gave it birth. This feature can be used to examine interactions between spaceships and other "objects" within the game.[1] Another similar variation, called QuadLife, involves four different ON states. When a new cell is born from three different ON neighbors, it takes on the fourth value, and otherwise like Immigration it takes the majority value. [2] Except for the variation among ON cells, both of these variations act identically to Life.
Variation for two players[modifica]
In this variation, live cells can have two colours and a player wins when all cells of the opponent's colour are eliminated. When a dead cell becomes live, its colour is determined by the dominating colour of its neighbour live cells (which are exactly three). Start with a random or pre-chosen starting pattern with half the live cells of each colour. After one iteration, the first player may add one cell of his colour and remove one cell of his opponent's colour. After the next iteration the other player can do the same, and so forth.
Notable Life programs[modifica]
As there are thousands of Life programs online, a full list will not be provided here. The following is a selection of a small number of programs with some special claim to notability, such as popularity or unusual features. Most of these programs incorporate a graphical user interface for pattern editing and simulation, the capability for simulating multiple rules including Life, and a large library of interesting patterns in Life and other CA rules.
- Conway's Game of Life by Alan Hensel. A pop-up Java web applet with fast simulation algorithms and a big library of interesting Life patterns.
- Golly. A cross-platform (Windows, Macintosh, and Linux) open-source Life simulation system by Andrew Trevorrow and Tomas Rokicki including the hashlife algorithm for extremely fast generation and Python scriptability for both editing and simulation.
- Life32. Freeware for Windows machines includes powerful and scriptable pattern editing features.
- Mirek's Cellebration. Free 1-D and 2-D Cellular Automata viewer, explorer and editor for Windows. Includes powerful facilities for simulating and viewing a wide variety of CA rules including Life, and a scriptable editor.
- Xlife A cellular-automaton laboratory by Jon Bennett. For a long time the standard Linux Life simulation application, and has also been ported to Windows. Can handle cellular automaton rules with the same neighborhood as Life and up to eight possible states per cell. See here for many alternative versions.
See also[modifica]
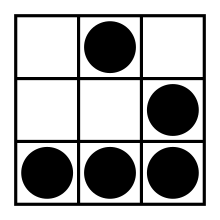
- Garden of Eden pattern
- Hashlife
- Life-like cellular automaton
- Puffer train
- Spaceship
- Hacker Emblem, depicting a glider
External links[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Meldor/Joc de la vida |
Many external links concerning the Game of Life can be found on Meldor/Joc de la vida a Curlie. In addition, Game of Life News is a blog reporting on recent developments in the Game of Life by many individuals.
Some additional links:
- Cellular Automata FAQ - Conway's Game of Life - Answers to frequently asked questions.
- Robert T. Wainwright's LIFEPAGE - From 1971 to 1973 Wainwright edited LIFELINE, an influential newsletter for enthusiasts. This site contains a downloadable copy of the first issue as well as an index.
- A Turing Machine in Conway's Game of Life - Describes an implementation of a Turing machine engineered from Game of Life pattern components.

