Estructura lineal dual
El mòdul dual i l'espai dual d'una estructura lineal bàsica (mòdul sobre un anell i espai vectorial sobre un cos, respectivament) és el conjunt de les seves formes lineals, juntament amb la seva estructura lineal corresponent. Quan el A-mòdul és lliure, les propietats del dual es confonen amb les de l'espai dual d'un espai vectorial, que no és altra cosa que un mòdul lliure sobre un cos.
Mòdul dual i espai dual[modifica]
Sigui M un A-mòdul per l'esquerra sobre un anell A. Sigui el conjunt de les formes lineals de M, és a dir, el conjunt d'homomorfismes de M en A considerat ell mateix com a A-mòdul per l'esquerra, amb l'acció de l'anell A sobre cadascuna de les formes de M donada per
Aleshores, és un A-mòdul per la dreta que s'anomena A-mòdul dual de M. En la notació habitual per a les formes lineals, l'acció de l'anell A sobre les formes de s'escriu
Si A és un cos, aleshores M és un espai vectorial i és un altre espai vectorial anomenat espai dual de l'espai M. Aleshores, les formes lineals d' se solen anomenar covectors.
Dualitat en mòduls lliures i espais vectorials[modifica]
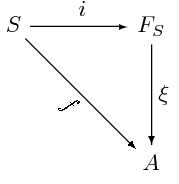
Si és el A-mòdul lliure sobre el conjunt de generadors S, per cada aplicació hi ha un homomorfisme únic que fa que el següent diagrama
sigui commutatiu. L'homomorfisme és una forma lineal del mòdul i, per tant, un element del mòdul dual . En conseqüència, i per causa de la unicitat de l'homomorfisme i de la commutativitat del diagrama anterior, el mòdul dual, es pot identificar amb el mòdul de les aplicacions de S en l'anell A, és a dir, amb el producte directe
d'una família d'exemplars de l'anell A indexada pel conjunt S. D'altra banda, el mòdul lliure es pot identificar amb la suma directa
d'una família d'exemplars de l'anell A indexada també pel conjunt S. Això implica que la cardinalitat del mòdul dual és estrictament més gran que la del mòdul lliure inicial, llevat que S sigui un conjunt finit, és a dir, si no és que és finitament generat. Els resultats anteriors són perfectament vàlids si A és un cos i, per tant, si és un espai vectorial amb l'afegitó que, com que l'espai dual és de cardinalitat més gran que la de l'espai inicial, la dimensió de l'espai dual és estrictament més gran que la de l'espai inicial si no és que aquesta dimensió és finita, cas en el qual són iguals.
Bases duals[modifica]
Considerem ara que el conjunt S és finit. Podem posar S = { 1, 2, ..., n }. Aleshores és un mòdul lliure finitament generat de rang n (o un espai vectorial de dimensió finita n, si A és un cos). Per cada aplicació
(emprant la notació de la delta de Kronecker) hi ha una forma lineal única que fa que el següent diagrama
sigui commutatiu. Amb la notació , el conjunt és una base de i l'acció de les n formes lineals del conjunt és .
Ara tenim que, si , per cada ,
i el conjunt és linealment independent. A més, com que és un mòdul lliure, tota forma lineal queda determinada pels seus valors a la base B. Si posem i és qualsevol, tenim
i, en conseqüència,
i genera el mòdul dual (espai dual) i, per tant, n'és una base. Aquesta base és la base dual de la base B.
Resulta, doncs, que els mòduls duals (respectivament espais duals) de mòduls lliures finitament generats (resp. espais vectorials de dimensió finita) tenen el mateix rang (resp. la mateixa dimensió) i, si l'anell A és commutatiu, són, per tant, isomorfs. Però aquest isomorfisme no és pas canònic, sinó que depèn de la base escollida.
En el cas de mòduls lliures no finitament generats (espais vectorials de dimensió infinita), el conjunt només genera un submòdul estricte (subespai estricte) del dual.
Formes bilineals i dualitat[modifica]
Sigui una forma bilineal dels dos mòduls M per l'esquerra i N per la dreta sobre un anell A, i siguin per la dreta i per l'esquerra els seus respectius mòduls duals. Aleshores es poden definir, de manera natural, les aplicacions lineals
donades per
això és
Si la forma bilineal ω és no degenerada, aleshores les aplicacions f i g són injectives, perquè ker f i ker g són els submòduls (subespais) nuls de la forma, els quals, per a una forma no degenerada, són nuls.
Si tant M com N són mòduls lliures de finitament generats (o espais vectorials de dimensió finita) la injectivitat de f i g implica
però com que són finitament generats,
cosa que implica que dim M = dim N i que f i g són isomorfismes. Per tant, es poden fer les identificacions i M i N són duals l'un de l'altre.
Si M = N i A és commutatiu, l'existència d'una forma bilineal no degenerada implica un isomorfisme entre M i el seu dual , però aquest isomorfisme no és pas canònic, perquè n'hi ha tants com matrius quadrades n×n no singulars es puguin formar amb elements de l'anell A.
El bidual[modifica]
Per a M i el seu dual, , podem definir la forma bilineal
que és òbviament no degenerada. Com ja s'ha mencionat més amunt, si M és de finitament generat (de dimensió finita), això implica l'isomorfime canònic
amb
i M i es poden considerar idèntics i i dual l'un de l'altre.
Vegeu també[modifica]
Referències[modifica]
- Schmitt, William. Notes on Modules and Algebras (en anglès), 2006.