Equacions de Maxwell

Les equacions de Maxwell són un conjunt de quatre equacions que descriuen completament els fenòmens electromagnètics. La gran contribució de James Clerk Maxwell fou reunir en aquestes equacions molts anys de resultats experimentals i investigacions teòriques, deguts a Coulomb, Gauss, Ampère, Faraday i altres, introduint els conceptes de camp i de corrent de desplaçament, i unificant els camps elèctrics i magnètics en un sol concepte: el camp electromagnètic. De les equacions de Maxwell, a més, es desprèn l'existència d'ones electromagnètiques propagant-se amb velocitat c, el valor numèric de la qual coincideix amb el valor de la velocitat de la llum en el buit, amb la qual cosa Maxwell va identificar la llum amb una ona electromagnètica, unificant l'òptica amb l'electromagnetisme.

Detall de les equacions

Llei de Gauss

Article principal: Llei de Gauss

Esquema on es veu una superfície amb una càrrega puntual a l'interior.

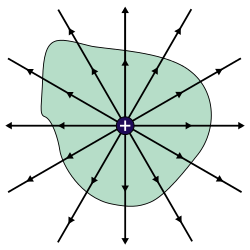
La llei de Gauss relaciona el flux del camp elèctric a través d'una superfície tancada amb la quantitat de càrrega que es troba a l'interior de la superfície.

Primer de tot, la definició del flux del camp elèctric $\Phi _{E}$ és la integral sobre tota la superfície tancada del vector $\mathrm {d} \mathbf {S}$ multiplicat escalarment pel vector camp elèctric $\mathbf {E}$:

$\Phi _{E}=\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {S}$

Per altra banda, hem dit que ens interessa la quantitat de càrrega a l'interior de la superfície tancada. Per tant, sigui $V$ el volum que està envoltat per la superfície $S$ - és a dir, que $S$ és la frontera de $V$: $S=\partial V$ - la càrrega total a l'interior de $S$ serà l'integral de volum de la densitat de càrrega $\rho$ :

$Q_{\mathrm {int} }=\int _{V}\;\rho \;\mathrm {d} V$

Un cop dit això, la llei de Gauss afirma que el flux del camp elèctric a través d'una superfície $S=\partial V$ és directament proporcional a la càrrega interior, i la constant de proporcionalitat és ${\frac {1}{\varepsilon _{0}}}$. Això escrit matemàticament és:

$\oint _{\partial V}\mathbf {E} \cdot \mathrm {d} \mathbf {S} ={\frac {Q_{\mathrm {int} }}{\varepsilon _{0}}}={\frac {1}{\varepsilon _{0}}}\int _{V}\;\rho \;\mathrm {d} V$

Que s'anomena la llei de Gauss en forma integral. En el cas del camp electroestàtic, aquesta fórmula es pot deduïr de la llei de Coulomb i viceversa. Tot i això, la llei de Gauss segueix sent vàlida en el cas electrodinàmic.

Demostració

A partir de la fórmula anterior, i aplicant el teorema de la divergència, obtindrem la llei de Gauss en forma diferencial. Vegem-ho:

${\frac {Q_{\mathrm {int} }}{\varepsilon _{0}}}=\int _{V}\;{\frac {\rho }{\varepsilon _{0}}}\;\mathrm {d} V=\oint _{\partial V}\mathbf {E} \cdot \mathrm {d} \mathbf {S} =\int _{V}\;\nabla \cdot \mathbf {E} \;\mathrm {d} V$

On hem aplicat el teorema de la divergència en l'últim pas. Com que això es compleix per qualsevol volum $V$, això implica que les dues quantitats de dins les integrals han de ser iguals, de manera que concluïm que:

$\nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}$

Formulació

La formulació moderna de les equacions de Maxwell és deguda a Oliver Heaviside i Josiah Willard Gibbs, que el 1884 reformularen les equacions originals de Maxwell en un sistema abreujat utilitzant notació vectorial. La formulació original de Maxwell datava de 1865 i contenia 20 equacions de 20 variables. La formulació vectorial resultava especialment atractiva perquè remarcava les simetries intrínseques en les equacions fent més fàcil la seva utilització.

Les equacions de Maxwell, en forma integral i diferencial són les següents (ambdues formes són totalment equivalents, es pot passar d'una a l'altra amb les eines habituals del càlcul diferencial).

Nom	Forma diferencial	Forma integral
Llei de Gauss	$\nabla \cdot \mathbf {D} =\rho$	$\oint _{S}\mathbf {D} \cdot \mathrm {d} \mathbf {S} =Q_{i}$
Llei de Gauss per al magnetisme	$\nabla \cdot \mathbf {B} =0$	$\oint _{S}\mathbf {B} \cdot \mathrm {d} \mathbf {S} =0$
Llei de Faraday:	$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$	$\oint _{\partial S}\mathbf {E} \cdot \mathrm {d} \mathbf {l} =-{\mathrm {d} \over \mathrm {d} t}\int _{S}\mathbf {B} \cdot \mathrm {d} \mathbf {S}$
Llei d'Ampère-Maxwell:	$\nabla \times \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}$	$\oint _{\partial S}\mathbf {H} \cdot \mathrm {d} \mathbf {l} =\int _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {S} +{\mathrm {d} \over \mathrm {d} t}\int _{S}\mathbf {D} \cdot \mathrm {d} \mathbf {S}$

• Q és la càrrega elèctrica (unitat SI: coulomb).
• ρ és la densitat de càrrega elèctrica (unitat SI: coulomb per metre cúbic), sense incloure càrregues dipolars lligades a un material.
• $\mathbf {B}$ és la inducció magnètica (unitat SI: tesla, volt × segon per metre quadrat) $\mathbf {B} =\mu _{0}\mathbf {H}$.
• $\mathbf {D}$ és el desplaçament elèctric (unitat SI: coulomb per metre quadrat) $\mathbf {D} =\varepsilon \mathbf {E}$.
• $\mathbf {S}$ és l'àrea de la superficie gaussiana d'integració.
• $\mathbf {E}$ és el camp elèctric (unitat SI: volt per metre).
• $\mathbf {H}$ és el camp magnètic (unitat SI: ampere per metre).
• $\mathbf {J}$ és la densitat de corrent elèctric (unitat SI: ampere per metre quadrat)
• $\nabla \cdot$ és l'operador divergència (unitat del SI: 1 per metre)
• $\nabla \times$ és l'operador rotacional (unitat del SI: 1 per metre)

Encara que es donen les unitats del sistema internacional d'unitats per a les diversos magnituds, les equacions de Maxwell es mantenen en altres sistemes d'unitats.

Interpretació física de les equacions

Les quatre equacions de Maxwell expressen, respectivament, com les càrregues elèctriques produeixen camps elèctrics (llei de Gauss), l'absència experimental de càrregues magnètiques (2a llei), com el corrent produeix camps magnètics (llei d'Ampère) i com els camps magnètics canviants produeixen camps elèctrics (llei de la inducció de Faraday).

Conservació de la càrrega

Article principal: Conservació de la càrrega

La conservació de la càrrega és un principi que estableix que no és possible crear ni destruir càrrega. Això vol dir que si en un punt hi ha una disminució de la densitat de càrrega, implica que també hi ha d'haver una divergència positiva de densitat de corrent, i viceversa.

Això pot ser resumit matemàticament en la següent expressió

${\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {J} =0$

que pot deduir-se fàcilment a partir de les lleis de Maxwell.

Demostració

Per fer la demostració, aplicarem l'operador divergència a la llei d'Ampère-Maxwell: $\nabla \cdot (\nabla \times \mathbf {H} )=\nabla \cdot \mathbf {J} +\nabla \cdot {\partial \mathbf {D} \over \partial t}$ Però tenint en compte que la divergència del rotacional és zero, tenim que: $\nabla \cdot \mathbf {J} +{\partial \over \partial t}(\nabla \cdot \mathbf {D} )=0$ Si apliquem la llei de Gauss obtenim $\nabla \cdot \mathbf {J} +{\partial \rho \over \partial t}=0$ tal i com volíem demostrar.

Aquesta expressió també es pot escriure en forma integral:

$\oint _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {S} =-{\frac {\mathrm {d} Q_{\mathrm {int} }}{\mathrm {d} t}}$

Que s'obté utilitzant el teorema de la divergència a l'expressió diferencial anterior.

Demostració

Primer de tot, notem que si tenim un volum $V$ que té per frontera una superfície $S=\partial V$, llavors es compleix que la càrrega interior al volum és $Q_{\mathrm {int} }=\int _{V}\rho \;\mathrm {d} V$ Així que si apliquem la integral de volum als dos costats de la condició de continuïtat en forma diferencial obtenim: $\int _{V}{\frac {\partial \rho }{\partial t}}\;\mathrm {d} V+\int _{V}\nabla \cdot \mathbf {J} \;\mathrm {d} V=\int _{V}0\;\mathrm {d} V=0$ Que reescriurem com: ${\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V}\rho \;\mathrm {d} V+\int _{V}\nabla \cdot \mathbf {J} \;\mathrm {d} V=0$ Fent servir el que hem dit al principi de la demostració pel primer sumand, i el Teorema de la divergència pel segon, obtenim: ${\frac {\mathrm {d} Q_{\mathrm {int} }}{\mathrm {d} t}}+\oint _{\partial V}\mathbf {J} \cdot \mathrm {d} \mathbf {S} =0$ Que tenint en compte que $\partial V=S$ és el que volíem demostrar.

Força de Lorentz

Les equacions de Maxwell expressen com les càrregues i corrents creen camps elèctrics i magnètics, però no com aquests camps actuen sobre la matèria. Per a això es necessita la llei de força de Lorentz:

$\mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )$

Aquesta llei ens diu quina força experimenta una càrrega puntual en moviment en el sí d'un camp electromagnètic. Si en lloc d'una càrrega puntual tenim una distribució de càrrega, la corresponent força per unitat de volum és:

$\mathbf {f} =\rho \mathbf {E} +\mathbf {J} \times \mathbf {B}$

i la resultant sobre tot el volum és la integral d'aquesta densitat estesa a tot el volum.

Equacions de Maxwell en el buit

Com que al buit no hi ha càrregues ni corrents, les equacions de Maxwell se simplifiquen considerablement i s'obté:

$\nabla \cdot \mathbf {E} =0$

$\nabla \cdot \mathbf {H} =0$

$\nabla \times \mathbf {E} =-\mu _{0}{\frac {\partial \mathbf {H} }{\partial t}}$

$\nabla \times \mathbf {H} =\ \ \varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}$

Aquest conjunt d'equacions té una solució simple en termes d'ones planes sinusoïdals que es propaguen, amb el camp elèctric i el magnètic oscil·lant en direcció perpendicular a la direcció de propagació i entre sí. La velocitat de propagació resulta ser

$c={\frac {1}{\sqrt {\mu _{0}\varepsilon _{0}}}}$

Maxwell descobrí que aquesta velocitat c és la velocitat de la llum en el buit i, per tant, que la llum és un tipus particular d'ona electromagnètica.

Les equacions de Maxwell en relativitat especial

En relativitat especial, per tal d'expressar més clarament que les equacions de Maxwell en el buit tenen la mateixa forma en qualsevol sistema de referència inercial, s'acostumen a escriure en termes de quadrivectors i tensors en forma covariant (en unitats cgs):

${4\pi \over c}J^{\beta }={\partial F^{\alpha \beta } \over {\partial x^{\alpha }}}\ {\stackrel {\mathrm {def} }{=}}\ \partial _{\alpha }F^{\alpha \beta }\ {\stackrel {\mathrm {def} }{=}}\ {F^{\alpha \beta }}_{,\alpha }\,\!$,

i

$0=\partial _{\gamma }F_{\alpha \beta }+\partial _{\beta }F_{\gamma \alpha }+\partial _{\alpha }F_{\beta \gamma }\ {\stackrel {\mathrm {def} }{=}}\ {F_{\alpha \beta }}_{,\gamma }+{F_{\gamma \alpha }}_{,\beta }+{F_{\beta \gamma }}_{,\alpha }\ {\stackrel {\mathrm {def} }{=}}\ \epsilon _{\delta \alpha \beta \gamma }{F^{\beta \gamma }}_{,\alpha }$

where $\,J^{\alpha }$ és el quadricorrent, $\,F^{\alpha \beta }$ és el tensor electromagnètic, $\,\epsilon _{\alpha \beta \gamma \delta }$ és el símbol de Levi-Civita i

${\partial \over {\partial x^{\alpha }}}\ {\stackrel {\mathrm {def} }{=}}\ \partial _{\alpha }\ {\stackrel {\mathrm {def} }{=}}\ {}_{,\alpha }\ {\stackrel {\mathrm {def} }{=}}\ \left({\frac {\partial }{\partial ct}},\nabla \right)$

és el quadrigradient. Els índexs repetits se sumen d'acord amb el conveni de sumació d'Einstein.

La primera equació tensorial expressa les dues equacions de Maxwell inhomogènies: la llei de Gauss i la d'Ampère amb les correccions de Maxwell. La segona equació expressa les altres dues equacions homogènies: la llei de Faraday de la inducció i la llei de Gauss per al camp magnètic (l'absència de monopols magnètics).

S'ha suggerit que el component vXB de la Força de Lorentz es pot derivar de la llai de Coulomb i la relativitat especial si hom assumeix la invariància de la càrrega elèctrica.

Vegeu també

• Força d'Abraham-Lorentz
• Fórmules de Fresnel