Monopol magnètic
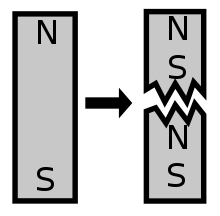
Un monopol magnètic no es pot crear a partir de matèria normal com àtoms i electrons, sinó que seria una nova partícula elemental.
En física de partícules, un monopol magnètic és una partícula elemental hipotètica que és un imant aïllat amb només un pol magnètic (un pol nord sense pol sud o viceversa).[1][2] Un monopol magnètic tindria una «càrrega magnètica» neta. L’interès modern pel concepte prové de les teories de les partícules, sobretot la gran teoria unificada i les supercordes, que prediuen la seva existència.[3][4]
El magnetisme en barres d'imants i electroimants no és causat per monopols magnètics i, de fet, no hi ha proves experimentals o observacionals conegudes que demostrin que existeixen monopols magnètics.
Alguns sistemes de matèria condensada contenen quasipartícules magnètiques monopolars efectives (no aïllades),[5] o contenen fenòmens que són matemàticament anàlegs als monopols magnètics.[6]
Antecedents històrics[modifica]
Ciències primerenques i física clàssica[modifica]
Molts primers científics van atribuir el magnetisme de les pedres imant a dos «fluids magnètics» diferents («efluvis»), un fluid que surt del pol nord en un extrem i un fluid surt del pol sud en l'altre, que s'atreuen i es repel·leixen mútuament per analogia a càrrega elèctrica negativa.[7][8] Tanmateix, una comprensió millorada de l'electromagnetisme al segle xix va demostrar que el magnetisme de les pedres imant no s’explicava adequadament pels fluids monopols magnètics, sinó per una combinació de corrents elèctrics, el moment magnètic dels electrons i els moments magnètics d’altres partícules. La llei de Gauss per al magnetisme, una de les equacions de Maxwell, és la afirmació matemàtica que no existeixen monopols magnètics. No obstant això, Pierre Curie va assenyalar el 1894[9] que els monopols magnètics podrien existir concebiblement, tot i no haver-se vist fins ara.
Mecànica quàntica[modifica]
La teoria quàntica de la càrrega magnètica va començar amb un article del físic Paul Dirac el 1931.[10] En aquest article, Dirac va demostrar que si existeixen monopols magnètics a l'Univers, llavors s'ha de quantificar tota la càrrega elèctrica de l'Univers (condició de quantificació de Dirac).[11] De fet, la càrrega elèctrica es quantifica, la qual cosa és coherent, però no demostra l'existència de monopols.[11]
Des de l’article de Dirac, s’han realitzat diverses recerques sistemàtiques dels monopols. Els experiments del 1975[12] i del 1982[13] van produir esdeveniments candidats que inicialment van ser interpretats com a monopols, però que ara es consideren poc concloents.[14] Per tant, continua sent una pregunta oberta si existeixen monopols. Altres avenços en la física teòrica de partícules, en particular els desenvolupament de la teoria de la gran unificació i la teoria de la gravetat quàntica, han conduït a arguments més convincents (que es detallen a continuació) sobre els monopols. Joseph Polchinski, teòric de cordes, va descriure l'existència de monopols com «una de les apostes més segures que es poden fer sobre la física que encara no s'ha vist».[15] Aquestes teories no són necessàriament incompatibles amb l'evidència experimental. En alguns models teòrics, és poc probable que s’observin monopols magnètics, ja que són massa massius per crear-los en acceleradors de partícules (vegeu Cerques de monopols magnètics a continuació) i també són massa rars a l’Univers per entrar en un detector de partícules amb molta probabilitat.[15]
Alguns sistemes de matèria condensada proposen una estructura superficialment similar a un monopol magnètic, conegut com a tub de flux. Els extrems d’un tub de flux formen un dipol magnètic, però, ja que es mouen de forma independent, es poden tractar per a molts propòsits com a quasipartícules de monopols magnètics independents. Des del 2009, nombrosos informes de premsa popular[16][17] han descrit incorrectament aquests sistemes com l'esperat descobriment dels monopols magnètics, però els dos fenòmens només es relacionen superficialment.[18][19] Aquests sistemes de matèria condensada continuen sent una àrea d'investigació activa. (Vegeu «Monopols» en sistemes de matèria condensada a continuació.)
Pols i magnetisme en matèria ordinària[modifica]
Tota la matèria aïllada fins ara, inclosos tots els àtoms de la taula periòdica i totes les partícules del model estàndard, té una càrrega monopòlica magnètica nul·la. Per tant, els fenòmens ordinaris de magnetisme i imants no deriven de monopols magnètics.
En canvi, el magnetisme en matèria ordinària es deu a dues fonts. En primer lloc, els corrents elèctrics creen camps magnètics segons la llei d’Ampère. En segon lloc, moltes partícules elementals tenen un moment magnètic intrínsec, el més important del qual és el moment dipolar elèctric de l'electró, que està relacionat amb el seu espín mecànic quàntic.
Matemàticament, el camp magnètic d’un objecte es descriu sovint en termes d’un desenvolupament multipolar. Aquesta és una expressió del camp com la suma de camps components amb formes matemàtiques específiques. El primer terme del desenvolupament s'anomena «terme monopolar», el segon es diu «dipol», després «quadrupol», després «octupol», etc. Qualsevol d'aquests termes pot estar present en el desenvolupament multipolar d'un camp elèctric, per exemple. No obstant això, en el desenvolupament multipolar d'un camp magnètic, el terme «monopol» sempre és exactament zero (per a matèria ordinària). Un monopol magnètic, si existeix, tindria la propietat definidora de produir un camp magnètic el terme de «monopol» del qual és diferent de zero.
Un dipol magnètic és una cosa el camp magnètic del qual és descrit predominantment o exactament pel terme «dipol magnètic» del desenvolupament multipolar. El terme «dipol» significa «dos pols», que corresponen al fet que un imant dipolar normalment conté un pol nord per un costat i un pol sud per l’altre costat. Això és anàleg a un dipol elèctric, que té càrrega positiva per un costat i càrrega negativa per l’altre. No obstant això, un dipol elèctric i un dipol magnètic són fonamentalment força diferents. En un dipol elèctric fet amb matèria ordinària, la càrrega positiva està formada per protons i la càrrega negativa està formada per electrons, però un dipol magnètic no té diferents tipus de matèria creant el pol nord i el pol sud. En canvi, els dos pols magnètics sorgeixen simultàniament de l'efecte agregat de tots els corrents i moments intrínsecs a tot l’imant. A causa d’això, els dos pols d’un dipol magnètic han de tenir sempre força igual i oposada, i els dos pols no es poden separar els uns dels altres.
Les equacions de Maxwell[modifica]
Les equacions de Maxwell de l'electromagnetisme relacionen els camps elèctrics i magnètics entre si i amb els moviments de les càrregues elèctriques. Les equacions estàndard proporcionen càrregues elèctriques, però no posseeixen càrregues magnètiques. Excepte aquesta diferència, les equacions són simètriques sota l'intercanvi dels camps elèctrics i magnètics.[notes 1] Les equacions de Maxwell són simètriques quan la càrrega i la densitat de corrent elèctrica són zero a tot arreu, com és el cas del buit.
Les equacions de Maxwell totalment simètriques també es poden escriure si es permet la possibilitat de «càrregues magnètiques» anàlogues a les càrregues elèctriques.[20] Amb la inclusió d’una variable per a la densitat d’aquestes càrregues magnètiques, per exemple ρm, també hi ha una variable de «densitat de corrent magnètica» a les equacions, jm.
Si no existeixen càrregues magnètiques (o si existeixen però no estan presents en una regió de l'espai), els nous termes de les equacions de Maxwell són tots zero, i les equacions desenvolupades es redueixen a les equacions convencionals de l'electromagnetisme, com ara ∇⋅B = 0 (on ∇⋅ és divergència i B és el camp magnètic B).
Dreta: En moviment (velocitat v), una càrrega elèctrica indueix un camp B mentre que una càrrega magnètica indueix un camp E. S'utilitza corrent convencional.
Part inferior esquerra: camp B a causa d'un matemàtic dipol magnètic m format per dos monopols magnètics.
Part inferior dreta: camp B a causa d'un moment dipolar magnètic m natural que es troba en matèria ordinària (no dels monopols magnètics). (No hi ha d'haver cercles vermells i blaus a la imatge inferior dreta.)
En unitats gaussianes[modifica]
Les equacions de Maxwell desenvolupades són, en unitats gaussianes, les següents:[23]
| Nom | Sense monopols magnètics | Amb monopols magnètics |
|---|---|---|
| Llei de Gauss | ||
| Llei del Gauss per al magnetisme | ||
| Llei de Faraday de la inducció | ||
| Llei d'Ampère (amb l'ampliació de Maxwel) | ||
| Llei de la Força de Lorentz[23][24] | ||
En aquestes equacions, ρm és la densitat de càrrega magnètica, jm és la densitat de corrent magnètica i qm és la càrrega magnètica d’una partícula de prova, tot definit de manera anàloga a les quantitats de càrrega i corrent elèctriques relacionades; v és la velocitat de la partícula i c és la velocitat de la llum. Per a la resta de definicions i detalls, vegeu les equacions de Maxwell. Per a les equacions en forma adimensionalitzada, s'eliminen els factors de c.
En Sistema Internacional d'Unitats[modifica]
En les unitats SI, hi ha dues definicions contradictòries en l'ús de la càrrega magnètica qm, amb unitats diferents: weber (Wb) i ampere-metre (A⋅m). La conversió entre ells és qm[Wb] = μ0qm[A⋅m], ja que les unitats són 1 Wb = 1 H⋅A = (1 H⋅m−1)(1 A⋅m) mitjançant anàlisi dimensional (H és el henry, la unitat SI d'inductància).
Les equacions de Maxwell adopten les formes següents (utilitzant la mateixa notació anterior):[notes 2]
| Nom | Sense monopols magnètics | Amb monopols magnètics | |
|---|---|---|---|
| Convenció en weber | Convenció en ampere-metre | ||
| Llei de Gauss | |||
| Llei de Gauss per al magnetisme | |||
| Llei de Faraday de la inducció | |||
| Llei d'Ampère (amb l'ampliació de Maxwell) | |||
| Equació de la Força de Lorentz | |||
Formulació en tensors[modifica]
Les equacions de Maxwell en el llenguatge dels tensors deixen clara l'invariància de Lorentz. Les equacions generalitzades són:[25][23]
| Equacions de Maxwell | Unitats gaussianes | SI d'unitats (Wb) | SI d'unitats (A⋅m) |
|---|---|---|---|
| Llei de Faraday-Gauss | |||
| Llei d'Ampère-Gauss | |||
| Llei de la Força de Lorentz |
on
- Fαβés el tensor electromagnètic, = 12εαβγδFγδ és el tensor electromagnètic dual,
- per a una partícula amb càrrega elèctrica qe i càrrega magnètica qm; v és la quadrivelocitat i p el quadrimoment,
- per a una distribució de càrrega elèctrica i magnètica; Je = (ρe, je) és el quadricorrent elèctric i Jm = (ρm, jm) el quadricorrent magnètic.
Per a una partícula que només té càrrega elèctrica, es pot expressar el seu camp mitjançant un quadripotencial, segons la formulació covariant estàndard de l'electromagnetisme clàssic:
Tanmateix, aquesta fórmula és inadequada per a una partícula que té càrrega tant elèctrica com magnètica, i hem d'afegir un terme que impliqui un altre potencial P.[26][27]
Aquesta fórmula per als camps sovint s’anomena relació Cabibbo-Ferrari, tot i que Shanmugadhasan la va proposar abans.[27] La quantitat εαβγδ és el símbol de Levi-Civita, i els índexs (com de costum) es comporten segons el conveni de sumació d'Einstein.
Transformació de la dualitat[modifica]
Les equacions generalitzades de Maxwell posseeixen una certa simetria, anomenada transformació de la dualitat. Es pot triar qualsevol angle real ξ i canviar simultàniament els camps i les càrregues de tot l’Univers de la manera següent (en unitats gaussianes):[28]
| Càrregues i corrents | Camps |
|---|---|
on les quantitats amb prima (′) són les càrregues i els camps abans de la transformació, i les quantitats sense prima són després de la transformació. Els camps i les càrregues després d'aquesta transformació segueixen obeint les mateixes equacions de Maxwell. La matriu és una matriu de rotació bidimensional.
A causa de la transformació de la dualitat, no es pot decidir de manera única si una partícula té una càrrega elèctrica, una càrrega magnètica o ambdues, només observant el seu comportament i comparant-ho amb les equacions de Maxwell. Per exemple, és simplement una convenció, no un requisit de les equacions de Maxwell, que els electrons tinguin càrrega elèctrica però no càrrega magnètica; després d'una transformació ξ =, seria al revés. El fet empíric clau és que totes les partícules observades tenen la mateixa relació de càrrega magnètica a càrrega elèctrica.[28] Les transformacions de dualitat poden canviar la proporció a qualsevol valor numèric arbitrari, però no poden canviar el fet que totes les partícules tinguin la mateixa proporció. Com que és el cas, es pot fer una transformació de la dualitat que estableixi aquesta relació a zero, de manera que totes les partícules no tinguin cap càrrega magnètica. Aquesta elecció es basa en les definicions «convencionals» d'electricitat i magnetisme.[28]
Quantització de Dirac[modifica]
Un dels avenços definitius en la teoria quàntica va ser el treball de Paul Dirac sobre el desenvolupament d'un electromagnetisme quàntic relativista. Abans de la seva formulació, la presència de càrrega elèctrica simplement «s'inseria» a les equacions de la mecànica quàntica (MQ), però el 1931 Dirac va demostrar que una càrrega discreta «cau» naturalment de la MQ. És a dir, podem mantenir la forma de les equacions de Maxwell i encara tenim càrregues magnètiques.
Penseu en un sistema que consisteix en un sol monopoli elèctric estacionari (un electró, per exemple) i un sol monopoli magnètic estacionari. Clàssicament, el camp electromagnètic que els envolta té una densitat d’impuls donada pel vector de Poynting, i també té un moment angular total, que és proporcional al producte qeqm i independent de la distància entre ells.
Però la mecànica quàntica dicta que el moment angular es quantifica en unitats de ħ, de manera que el producte qeqm també s'ha de quantitzar. Això significa que si fins i tot existís un sol monopol magnètic a l'Univers i la forma de les equacions de Maxwell sigui vàlida, totes les càrregues elèctriques es quantitzarien.
Quines són les unitats en què es quantitzaria la càrrega magnètica? Tot i que seria possible simplement integrar-se en tot l'espai per trobar el moment angular total en l'exemple anterior, Dirac va adoptar un enfocament diferent. Això el va portar a noves idees. Va considerar una càrrega magnètica similar a un punt el camp magnètic del qual es comporta com qm / r 2 i es dirigeix en la direcció radial, situada a l'origen. Com que la divergència de B és igual a zero gairebé a tot arreu, excepte el lloc del monopol magnètic a r = 0, es pot definir localment el potencial vectorial de manera que l'operador nabla del potencial vectorial A sigui igual al camp magnètic B.
Tot i així, el potencial vectorial no es pot definir globalment amb precisió perquè la divergència del camp magnètic és proporcional a la funció delta de Dirac a l’origen. Hem de definir un conjunt de funcions per al potencial vectorial a «l'hemisferi nord» (el semiespai z > 0 sobre la partícula), i un altre conjunt de funcions per a «l'hemisferi sud». Aquests dos potencials vectorials coincideixen a «l'equador» (el pla z = 0 a través de la partícula), i es diferencien per una transformació de gauge. La funció d'ona d'una partícula carregada elèctricament (una «càrrega sonda») que orbita al voltant de «l'equador» generalment canvia per una fase, de la mateixa manera que en l'efecte Aharonov-Bohm. Aquesta fase és proporcional a la càrrega elèctrica qe de la sonda, així com a la càrrega magnètica qm de la font. Dirac originalment estava considerant un electró la funció d'ona del qual va descriure en l'equació de Dirac.
Com que l'electró torna al mateix punt després del viatge complet al voltant de l'equador, la fase φ de la seva funció d’ona eiφ ha d’estar sense canvis, la qual cosa implica que la fase φ afegida a la funció d’ona ha de ser múltiple de :
| Unitats | Condició |
|---|---|
| Unitats gaussianes | |
| SI d'unitats (Wb)[29] | |
| SI d'unitats (A⋅m) |
on ε0 és la permitivitat del buit, ħ = h / 2 és la constant de Planck reduïda, c és la velocitat de la llum i ℤ és el conjunt de nombres enters.
Això es coneix com a condició de quantització de Dirac. La hipotètica existència d’un monopol magnètic implicaria que la càrrega elèctrica s’ha de quantificar en determinades unitats; també, l'existència de càrregues elèctriques implica que les càrregues magnètiques dels hipotètics monopols magnètics, si existeixen, s'han de quantificar en unitats inversament proporcionals a la càrrega elèctrica elemental.
En aquell moment no estava clar si existia tal cosa o fins i tot si calia fer-ho. Al cap i a la fi, podria aparèixer una altra teoria que explicaria la quantització de càrregues sense necessitat del monopol. El concepte seguia sent una curiositat. No obstant això, en el temps transcorregut des de la publicació d’aquest treball, no ha aparegut cap altra explicació àmpliament acceptada sobre la quantització de càrregues. (El concepte d’invariancia local del calibre (vegeu teoria de gauge) proporciona una explicació natural de la quantització de càrregues, sense invocar la necessitat de monopols magnètics; però només si el grup del gauge U(1) és compacte, en aquest cas tenim de totes maneres monopols magnètics.)
Si ampliem al màxim la definició del potencial vectorial per a l’hemisferi sud, es defineix a tot arreu, excepte una línia semi-infinita estesa des de l’origen en direcció al pol nord. Aquesta línia semi-infinita s’anomena cadena de Dirac i el seu efecte sobre la funció d’ona és anàleg a l'efecte del solenoide en l'efecte Aharonov-Bohm. La condició de quantització prové del requisit que les fases al voltant de la cadena de Dirac siguin trivials, el que significa que la cadena de Dirac ha de ser poc física. La cadena Dirac és només un artefacte del gràfic de coordenades utilitzat i no s’ha de prendre seriosament.
El monopol de Dirac és una solució singular de l'equació de Maxwell (perquè requereix eliminar la línia del món de l'espaitemps); en teories més complicades, és substituïda per una solució suau com el monopol de 't Hooft-Polyakov.
Interpretació topològica[modifica]
Corda de Dirac[modifica]
Una teoria de gauge com l'electromagnetisme es defineix mitjançant un camp de gauge, que associa un element grupal a cada ruta en l'espaitemps. Per als camins infinitesimals, l'element del grup és proper a la identitat, mentre que per als camins més llargs, l'element del grup és el producte successiu dels elements del grup infinitesimal al llarg del camí.
En electrodinàmica, el grup és U(1), nombres complexos unitaris multiplicats. Per als camins infinitesimals, l'element de grup és 1 + iAμdxμ el que implica que per als camins finits parametritzats per s, l'element de grup és:
El mapa des de camins fins a elements de grup s’anomena bucle de Wilson o holonomia, i per a un grup de gauge U(1) és el factor de fase que adquireix la funció d’ona d’una partícula carregada a mesura que travessa el camí. Per a un bucle:
De manera que la fase que obté una partícula carregada quan entra en un bucle és el flux magnètic a través del bucle. Quan un solenoide petit té un flux magnètic, hi ha franges d’interferència per a les partícules carregades que van al voltant del solenoide o al voltant de diferents costats del solenoide, que revelen la seva presència.
Però si totes les càrregues de les partícules són múltiples enters d’e, els solenoides amb un flux de 2π/e no tenen franges d’interferència, perquè el factor de fase de qualsevol partícula carregada és exp(2πi) = 1. Tal solenoide, si és prou prim, és invisible quànticament-mecànicament. Si aquest solenoide portés un flux de 2π/e, quan el flux sortís d’un dels seus extrems, no es distingiria d’un monopol.
De fet, la solució monopol de Dirac descriu un solenoide de línia infinitesimal que acaba en un punt i la ubicació del solenoide és la part singular de la solució, la cadena de Dirac. Les cadenes de Dirac enllacen monopols i antimonopols de càrrega magnètica oposada, tot i que, en la versió de Dirac, la cadena només va a l'infinit. La cadena no es pot observar, de manera que es pot posar a qualsevol lloc i, mitjançant desplaçament de coordenades, es pot fer que el camp de cada desplaçament sigui singular fent lliscar la cadena fins on no es pugui veure.
Teories de la gran unificació[modifica]
En un grup de gauge U(1) amb càrrega quantitzada, el grup és un cercle de radi 2π/e. Aquest grup de gauge U(1) s’anomena compacte. Qualsevol U(1) que prové d’una gran teoria unificada és compacte, perquè només tenen sentit els grups compactes de gauge superior. La mida del grup de guage és una mesura de la constant d’acoblament invers, de manera que en el límit d’un grup de gauge de gran volum, la interacció de qualsevol representació fixa tendeix a zero.
El cas del grup de gauge U(1) és un cas especial perquè totes les seves representacions irreductibles tenen la mateixa mida (la càrrega és més gran per una quantitat sencera, però el camp encara és només un nombre complex) de manera que el grup de gauge U(1) en la teoria de camps és possible prendre el límit descompactificat sense contradicció. La quantització de la càrrega es fa petita, però cada partícula carregada té un gran nombre de quanta de càrrega, de manera que la seva càrrega es manté finita. En una teoria de grups de gauge U(1) no compacta, les càrregues de les partícules genèricament no són múltiples enters d'una sola unitat. Atès que la quantització de càrregues és una certesa experimental, és clar que el grup gauge U(1) de l'electromagnetisme és compacte.
Les grans teories unificades (GTU) condueixen a grups compactes de gauge U(1), de manera que expliquen la quantització de càrregues d’una manera que sembla lògicament independent dels monopols magnètics. No obstant això, l'explicació és essencialment la mateixa, perquè en qualsevol GTU que es divideix en un grup de gauge U(1) a llargues distàncies, hi ha monopols magnètics.
L'argument és topològic:
- L'holonomia dels mapes de camp de gauge es fa en bucles a elements del grup de gauge. Els bucles infinitesimals es mapejen per agrupar elements infinitesimalment propers a la identitat.
- Si es imagina una gran esfera a l'espai, es pot deformar un bucle infinitesimal que comença i acaba al pol nord de la següent manera: estirar el bucle sobre l’hemisferi occidental fins que esdevingui un gran cercle (que encara comença i acaba al pol nord) i deixar que es redueixi a un petit bucle mentre passa per l’hemisferi oriental. D’això s’anomena llaçar l'esfera.
- El llaçar és una seqüència de bucles, de manera que l'holonomia el mapeja a una seqüència d'elements de grup, un camí continu del grup d'indicadors. Com que el bucle al començament del llaçament és el mateix que el bucle al final, el camí del grup tancat.
- Si el recorregut del grup associat al procediment de llaçament s’enrotlla al voltant de l’U(1), l'esfera conté càrrega magnètica. Durant el llaçament, l'holonomia canvia per la quantitat de flux magnètic a través de l'esfera.
- Com que l'holonomia al principi i al final és la identitat, es quantifica el flux magnètic total. La càrrega magnètica és proporcional al nombre de voltes del fil de la bobina N, el flux magnètic a través de l'esfera és igual a 2N/e. Aquesta és la condició de quantificació de Dirac, i és una condició topològica que exigeix que les configuracions de camp de gauge U(1) de llarga distància siguin coherents.
- Quan el grup de gauge U(1) prové de trencar un grup de Lie compacte, el camí que serpenteja al voltant del grup U(1) prou vegades és topològicament trivial al grup gran. En un grup de Lie compacte no-U(1), l'espai que cobreix és un grup de Lie amb la mateixa àlgebra de Lie, però on tots els bucles tancats són contractables. Els grups de Lie són homogenis, de manera que qualsevol cicle del grup es pot moure de manera que comenci a la identitat, després el seu ascens al grup de cobertura acaba a P, que és un ascens de la identitat. Donar la volta al bucle dues vegades et porta a P², tres vegades a P3, tots els ascensors de la identitat. Però només hi ha un nombre infinit d'ascensors de la identitat, perquè els ascensors no es poden acumular. Aquest nombre de vegades que s'ha de travessar el bucle per fer-lo contràctil és petit, per exemple, si el grup GTU és SO(3), el grup de cobertura és SU(2) i n'hi ha prou amb donar la volta a qualsevol bucle dues vegades.
- Això vol dir que hi ha una configuració de camp de gauge contínua al grup de GTU que permet que la configuració del monopol U(1) es desenvolupi a distàncies curtes, a costa de no quedar-se a al U(1). Per fer-ho amb la menor energia possible, s'hauria de deixar només el grup de gauge U(1) al voltant d'un punt, que s'anomena nucli del monopol. Fora del nucli, el monopoli només té energia de camp magnètic..
Per tant, el monopoli de Dirac és un defecte topològic en una teoria de gauge compacte U(1). Quan no hi ha una gran teoria unificada, el defecte és una singularitat: el nucli es redueix fins a un punt. Però quan hi ha algun tipus de regulador de curta distància en l'espaitemps, els monopols tenen una massa finita. Els monopols es produeixen a la xarxa U(1), i allà la mida del nucli és la mida de la xarxa. En general, s’espera que es produeixin sempre que hi hagi un regulador de curta distància.
Teoria de cordes[modifica]
A l'Univers, la gravetat quàntica proporciona el regulador. Quan s’inclou la gravetat, la singularitat del monopol pot ser un forat negre i, per a una gran càrrega i massa magnètica, la massa del forat negre és igual a la càrrega del forat negre, de manera que la massa del forat negre magnètic no és infinita. Si el forat negre pot decaure completament per radiació de Hawking, les partícules carregades més lleugeres no poden ser massa pesades.[30] El monopol més lleuger hauria de tenir una massa inferior o comparable a la seva càrrega en unitats naturals.
Així doncs, en una teoria hologràfica consistent, de la qual la teoria de cordes és l’únic exemple conegut, sempre hi ha monopols de massa finita. Per a l'electromagnetisme ordinari, el límit de massa superior no és molt útil perquè té aproximadament la mateixa mida que la massa de Planck.
Formulació matemàtica[modifica]
En matemàtiques, un camp de gauge (clàssic) es defineix com una connexió sobre un G-fibrat principal sobre l'espaitemps. G és el grup gauge i actua per separat sobre cada fibrat del paquet.
Una connexió en un G-fibrat us indica com enganxar fibrats junts en punts propers de M. Comença amb un grup de simetria contínua G que actua sobre el fibrat F i, a continuació, associa un element grupal a cada camí infinitesimal. La multiplicació de grups al llarg de qualsevol camí us indica com passar d’un punt del fibrat a un altre, tenint l'element G associat a un camí que actua sobre la fibra F.
En matemàtiques, la definició de fibrat està dissenyada per emfatitzar la topologia, de manera que la noció de connexió s’afegeix com a reflexió posterior. En física, la connexió és l'objecte físic fonamental. Una de les observacions fonamentals en la teoria de classes característiques en topologia algebraica és que moltes estructures homotopiques de feixos principals no trivials es poden expressar com una integral d'algun polinomi sobre qualsevol connexió sobre aquest. Tingueu en compte que una connexió a través d’un fbrat trivial mai no ens pot proporcionar un fibrat principal no trivial.
Si l'espaitemps és ℝ4, es connecta l'espai de totes les connexions possibles del G-fibrat. Però tingueu en compte què passa quan eliminem una línia d'univers com el temps de l'espaitemps. L'espaitemps resultant és homotòpicament equivalent a l'esfera topològica S².
Un G-fibrat principal sobre S² es defineix cobrint S² per dues cartes, cadascuna homeomorfa a la 2-bola oberta de manera que la seva intersecció sigui homeomorfa amb la franja S¹ × I. Les 2-boles són homotòpicament trivials i la tira és homotòpicament equivalent al cercle S¹. Per tant, una classificació topològica de les possibles connexions es redueix a classificar les funcions de transició. La funció de transició assigna la tira a G, i les diferents maneres de mapejar una tira a G ve donada pel primer grup d’homotòpia de G.
Així doncs, en la formulació del G-fibrat, una teoria de gauge admet monopols de Dirac sempre que G no estigui connectat simplement, sempre que hi ha camins que van al voltant del grup que no es poden deformar a un camí constant (un camí el qual la imatge del qual consisteix en un sol punt). U(1), que té càrregues quantitzades, no està simplement connectat i pot tenir monopols de Dirac mentre que ℝ, el seu grup universal de cobertura, està simplement connectat, no té càrregues quantitzades i no admet monopols de Dirac. La definició matemàtica és equivalent a la definició de física sempre que, seguint Dirac, es permetin camps de gauge que només es defineixen de manera correcta i que el camp de gauge de diferents pegats quedi enganxat després d'una transformació de gauge.
El flux magnètic total no és altre que el primer nombre de Chern del paquet principal i depèn només de l'elecció del paquet principal i no de la connexió específica sobre aquest. En altres paraules, és un invariant topològic.
Aquest argument per als monopols és una reformulació de l'argument lasso per a una teoria pura d'U(1). Generalitza a d + 1 dimensions amb d ≥ 2 de diverses maneres. Una manera és estendre-ho tot a les dimensions addicionals, de manera que els monopols U(1) es converteixin en fulls de dimensió d - 3. Una altra manera és examinar el tipus de singularitat topològica en un punt amb el grup d’homotopia d − 2(G).
Teories de la gran unificació[modifica]
En els darrers anys, una nova classe de teories també ha suggerit l'existència de monopols magnètics.
A principis de la dècada del 1970, els èxits de la teoria dels camps quàntics i la teoria de gauge en el desenvolupament de la teoria electrofeble i les matemàtiques de la força nuclear forta van portar a molts teòrics a intentar combinar-los en una única teoria coneguda com a Gran Teoria Unificada (GTU). Es van proposar diverses GTU, la majoria de les quals implicaven la presència d’una partícula de monopol magnètic real. Més exactament, les GTU van predir un ventall de partícules conegudes com a dions, dels quals l'estat més bàsic era un monopol. La càrrega en monopols magnètics predits per la GTU és d'1 o 2 gD, depenent de la teoria.
La majoria de les partícules que apareixen en qualsevol teoria dels camps quàntics són inestables i decauen en altres partícules en diverses reaccions que han de complir diverses lleis de conservació. Les partícules estables són estables perquè no hi ha partícules més lleugeres en les quals puguin decaure i encara compleixin les lleis de conservació. Per exemple, l'electró té un nombre leptònic d’un i una càrrega elèctrica d’un, i no hi ha partícules més lleugeres que conservin aquests valors. D'altra banda, el muó, essencialment un electró pesat, pot decaure en l'electró més dos quanta d'energia i, per tant, no és estable.
Els dions en aquestes GTU també són estables, però per una raó completament diferent. S'espera que els dions existeixin com a efecte secundari de la «congelació» de les condicions de l'univers primerenc, o una ruptura de simetria. En aquest escenari, els dions sorgeixen a causa de la configuració del buit en una àrea determinada de l'Univers, segons la teoria original de Dirac. Es mantenen estables no per una condició de conservació, sinó perquè no hi ha un estat topològic més senzill en què puguin decaure.
L'escala de longitud sobre la qual existeix aquesta configuració especial de buit s'anomena longitud de correlació del sistema. Una longitud de correlació no pot ser superior a la que permetria la causalitat, per tant la longitud de correlació per fer monopols magnètics ha de ser almenys tan gran com la mida de l'horitzó determinat per la mètrica de l'Univers en expansió. Segons aquesta lògica, hi hauria d’haver almenys un monopol magnètic per volum d’horitzó tal com era quan es va produir el trencament de la simetria.[31]
Els models cosmològics dels esdeveniments posteriors al Big Bang fan prediccions sobre quin era el volum de l'horitzó, que condueixen a prediccions sobre la densitat de monopols actuals. Els primers models van predir una enorme densitat de monopols, en clara contradicció amb l'evidència experimental.[32][33]
Això es va anomenar el «problema del monopol». La seva resolució àmpliament acceptada no va ser un canvi en la predicció de la física de partícules dels monopols, sinó en els models cosmològics utilitzats per inferir la seva densitat actual. Concretament, les teories més recents de la inflació còsmica redueixen dràsticament el nombre previst de monopols magnètics, a una densitat prou petita com per fer que no sigui sorprenent que els humans no n’hagin vist mai cap.[34] Aquesta resolució del «problema del monopol» es va considerar com un èxit de la teoria de la inflació còsmica (tanmateix, per descomptat, només és un èxit notable si la predicció del monopol de la física de partícules és correcta).[35] Per aquestes raons, els monopols es van convertir en un gran interès les dècades del 1970 i 1980, juntament amb les altres prediccions «accessibles» de les GTU, com ara desintegració dels protons.
Moltes de les altres partícules predites per aquestes GTU van estar més enllà de les capacitats dels experiments actuals per detectar. Per exemple, es preveu que una àmplia classe de partícules conegudes com a bosons X i Y mediaran l'acoblament de les forces fortes i electrodèbils, però aquestes partícules són extremadament pesades i superen les capacitats raonables de qualsevol accelerador de partícules creat.
Cerques de monopols magnètics[modifica]
Les cerques experimentals de monopols magnètics es poden situar en una de dues categories: les que intenten detectar monopols magnètics preexistents i les que intenten crear i detectar nous monopols magnètics.
El pas d’un monopol magnètic a través d’una bobina de filferro indueix un corrent net a la bobina. Aquest no és el cas d’un dipol magnètic o d’un pol magnètic d’ordre superior, per al qual el corrent induït net és zero i, per tant, l'efecte es pot utilitzar com a prova inequívoca de la presència de monopols magnètics. En un cable amb resistència finita, el corrent induït dissipa ràpidament la seva energia com a calor, però en un bucle superconductor el corrent induït és de llarga durada. Mitjançant l’ús d’un «dispositius superconductors d'interferència quàntica» (SQUID) altament sensible, en principi es pot detectar fins i tot un sol monopol magnètic.
Segons la cosmologia inflacionària estàndard, els monopols magnètics produïts abans de la inflació s’haurien diluït fins a una densitat extremadament baixa. Els monopols magnètics també es poden haver produït tèrmicament després de la inflació, durant el període de reescalfament. No obstant això, els límits actuals de la temperatura de reescalfament abasten 18 ordres de magnitud i, en conseqüència, la densitat dels monopols magnètics actuals no està ben limitada per la teoria.
Hi ha hagut moltes cerques de monopols magnètics preexistents. Tot i que hi ha hagut un esdeveniment captivador registrat, per Blas Cabrera Navarro la nit del 14 de febrer de 1982 (per tant, de vegades referit com el «monopoli de Sant Valentí»),[36] mai no hi ha hagut proves reproduïbles de l'existència de monopols magnètics.[13] La manca d’aquests esdeveniments posa un límit superior al nombre de monopols d’aproximadament un monopol per 1029 nucleons.
Un altre experiment realitzat el 1975 va resultar en l’anunci de la detecció d’un monopol magnètic en moviment en raigs còsmics per part de l'equip dirigit per P. Buford Price.[12] Price va retirar la seva reclamació més tard i Álvarez va oferir una possible explicació alternativa.[37] En el seu article es va demostrar que el recorregut de l'esdeveniment de raigs còsmics que es va afirmar a causa d'un monopol magnètic es podia reproduir mitjançant el recorregut seguit d'un nucli de platí que decaia primer a osmi i després al tàntal.
S'han utilitzat col·lisionadors de partícules d'alta energia per intentar crear monopols magnètics. A causa de la conservació de la càrrega magnètica, cal crear monopols magnètics per parelles, un al nord i un al sud. A causa de la conservació de l'energia, només es poden produir monopols magnètics amb masses inferiors a la meitat del centre d'energia massiva de les partícules que col·lisionen. Més enllà d'això, se sap molt poc teòricament sobre la creació de monopols magnètics en col·lisions de partícules d'alta energia. Això es deu a la seva gran càrrega magnètica, que invalida totes les tècniques de càlcul habituals. Com a conseqüència, les recerques basades en col·lisionadors de monopols magnètics encara no poden proporcionar límits inferiors a la massa dels monopols magnètics. No obstant això, poden proporcionar límits superiors a la probabilitat (o secció transversal) de producció de parells, en funció de l'energia.
L’experiment ATLAS del Gran Col·lisionador d’Hadrons té actualment els límits de secció transversal més estrictes per a monopols magnètics d’1 i 2 càrregues de Dirac, produïts mitjançant la producció de parells Drell-Yan. Un equip dirigit per Wendy Taylor busca aquestes partícules basant-se en teories que les defineixen com de vida llarga (no decauen ràpidament), a més de ser altament ionitzants (la seva interacció amb la matèria és predominantment ionitzant). El 2019, la cerca de monopols magnètics al detector ATLAS va informar dels seus primers resultats a partir de les dades recollides de les col·lisions LHC Run 2 al centre d’energia de massa de 13 TeV, que a 34,4 fb−1 és el conjunt de dades més gran analitzat fins ara.[38]
L’experiment MoEDAL, instal·lat al Gran Col·lisionador d’Hadrons, està buscant actualment monopols magnètics i grans partícules supersimètriques mitjançant detectors de pistes nuclears i barres d'alumini al voltant del detector VELO (Vertex Locator) de LHCb. Les partícules es poden veure en les làmines de plàstic que formen els detectors de pistes nuclears al llarg del seu recorregut, amb diverses característiques identificatives. A més, les barres d'alumini poden atrapar els monopols magnètics que es mouen prou lentament. Les barres es poden analitzar passant-les per un SQUID (dispositius superconductors d'interferència quàntica).
L'astrofísic rus Ígor Nóvikov afirma que els camps magnètics dels forats negres macroscòpics són possibles monopols magnètics, que representen l'entrada a un pont d'Einstein-Rosen.[39]
«Monopols» en sistemes de matèria condensada[modifica]
Des de l'any 2003, diversos grups de física de la matèria condensada han utilitzat el terme «monopol magnètic» per descriure un fenomen diferent i en gran part no relacionat.[18][19]
Un veritable monopol magnètic seria una nova partícula elemental i violaria la llei de Gauss per al magnetisme ∇⋅B = 0. Un monopol d’aquest tipus, que ajudaria a explicar la llei de quantització de càrrega tal com va ser formulat per Paul Dirac el 1931,[40] mai no ha observats en experiments.[41][42]
Els monopols estudiats per grups de matèria condensada no tenen cap d’aquestes propietats. No són una partícula elemental nova, sinó que són un fenomen emergent en sistemes de partícules quotidianes (protons, neutrons, electrons, fotons); en altres paraules, són quasipartícules. No són fonts del camp B (és a dir, no infringeixen ∇⋅B = 0); en el seu lloc, són fonts per a altres camps, per exemple el camp H,[5] el camp B* (relacionat amb la vorticitat superfluida)[6][43] o diversos altres camps quàntics.[44] No són directament rellevants per a les grans teories unificades o altres aspectes de la física de partícules, i no ajuden a explicar la quantització de càrregues, tret que els estudis de situacions anàlogues puguin ajudar a confirmar que les anàlisis matemàtiques implicades són sòlides.[45]
Hi ha una sèrie d’exemples en la física de la matèria condensada on el comportament col·lectiu condueix a fenòmens emergents que s’assemblen als monopols magnètics en certs aspectes,[17][46][47][48] incloent-hi els materials amb gel de spin.[5][49] Tot i que aquests no s’han de confondre amb hipotètics monopols elementals existents al buit, no obstant això, tenen propietats similars i es poden investigar mitjançant tècniques similars.
Alguns investigadors utilitzen el terme magnetricitat per descriure la manipulació de monopols magnètics en quasipartícules en el gel de spin,[49][50][51][52] en analogia amb la paraula «electricitat».
Un exemple del treball sobre quasipartícules de monopols magnètics és un article publicat a la revista Science el setembre de 2009, en què els investigadors descrivien l’observació de quasipartícules semblants a monopols magnètics. Es va refredar un sol cristall de gel de espin a partir de titanat de disprosi a una temperatura entre 0,6 K i 2,0 K. Utilitzant observacions de dispersió de neutrons, es va demostrar que els moments magnètics s’alineaven en feixos de tubs entrellaçats que s’assemblen a cordes de Dirac. En el defecte format per l'extrem de cada tub, el camp magnètic té l’aspecte d’un monopol. Mitjançant un camp magnètic aplicat per trencar la simetria del sistema, els investigadors van ser capaços de controlar la densitat i l’orientació d’aquestes cadenes. També es va descriure una contribució a la capacitat tèrmica del sistema a partir d’un gas efectiu d’aquestes quasipartícules.[16][53] Aquesta investigació va guanyar el Premi Europhysics 2012 de física de la matèria condensada.
En un altre exemple, un article publicat a la revista Nature Physics de l’11 de febrer de 2011 descriu la creació i la mesura de corrents de quasipartícules de monopol magnètic de llarga vida en gel de spin. En aplicar un pols de camp magnètic al cristall de titanat de disprosi a 0,36 K, els autors van crear un corrent magnètic relaxant que va durar diversos minuts. Van mesurar el corrent mitjançant la força electromotriu que induïa en un solenoide acoblat a un amplificador sensible i el van descriure quantitativament mitjançant un model cinètic químic de càrregues puntuals que obeïen el mecanisme d'Onsager-Wien de dissociació i recombinació de portadors. D’aquesta manera, van derivar els paràmetres microscòpics del moviment del monopol en el spin de gel i van identificar els diferents papers de les càrregues magnètiques lliures i enllaçades.[51]
En els superfluids, hi ha un camp B*, relacionat amb la vorticitat dels superfluids, que és matemàticament anàleg al camp magnètic B. A causa de la similitud, el camp B* s'anomena «camp magnètic sintètic». Al gener de 2014, es va informar que es van crear i estudiar quasipartícules monopòliques[54] per al camp B* en un condensat Bose-Einstein.[6] Aquest constitueix el primer exemple d'un monopol quasi-magnètic observat dins d'un sistema governat per la teoria dels camps quàntics.[45]
Notes[modifica]
- ↑ El fet que els camps elèctrics i magnètics es puguin escriure de manera simètrica és específic del fet que l'espai és tridimensional. Quan les equacions de l'electromagnetisme s’extrapolen a altres dimensions, el camp magnètic es descriu com un tensor antisimètric de rang dos, mentre que el camp elèctric continua sent un veritable vector. En dimensions diferents de tres, aquests dos objectes matemàtics no tenen el mateix nombre de components.
- ↑ Per a la convenció on la càrrega magnètica té unitats de weber, vegeu Jackson (1999). En particular, per a les equacions de Maxwell, vegeu la secció 6.11, equació (6.150), pàgina 273, i per a la llei de la força de Lorentz, vegeu la pàgina 290, exercici 6.17 (a). Per a la convenció en què la càrrega magnètica té unitats d'ampere-metre, vegeu arXiv:physics/0508099v1, qm (4), per exemple.
Referències[modifica]
- ↑ Hooper, 2009.
- ↑ «Particle Data Group summary of magnetic monopole search» (
 PDF) (en anglès). lbl.gov.
PDF) (en anglès). lbl.gov.
- ↑ Wen, Xiao-Gang; Witten, Edward «Electric and magnetic charges in superstring models» (en anglès). Nuclear Physics B, 261, pàg. 651-677.
- ↑ Coleman, S. The Magnetic Monopole 50 years Later (reimprès en Aspects of Symmetry' (en anglès).
- ↑ 5,0 5,1 5,2 Castelnovo, C.; Moessner, R.; Sondhi, S. L. «Magnetic monopoles in spin ice» (en anglès). Nature, 451(7174), 03-01-2008, pàg. 42-45. arXiv: 0710.5515. Bibcode: 2008Natur.451...42C. DOI: 10.1038/nature06433. PMID: 18172493.
- ↑ 6,0 6,1 6,2 Ray et al., Hall, p. 657-660.
- ↑ Chisholm, 2018.
- ↑ Magie, 2018.
- ↑ Curie, 1894, p. 76-77.
- ↑ Dirac, 1931.
- ↑ 11,0 11,1 Littlejohn, Robert. «Lecture notes» (
 PDF) (en anglès). University of California, Berkeley, 2007-2008. Arxivat de l'original el 2011-07-19. [Consulta: 15 novembre 2021].
PDF) (en anglès). University of California, Berkeley, 2007-2008. Arxivat de l'original el 2011-07-19. [Consulta: 15 novembre 2021].
- ↑ 12,0 12,1 Price, P. B; Shirk, E. K; Osborne, W. Z; Pinsky, L. S «Evidence for Detection of a Moving Magnetic Monopole» (en anglès). Physical Review Letters, 35(8), 25-08-1975, pàg. 487-490. Bibcode: 1975PhRvL..35..487P. DOI: 10.1103/PhysRevLett.35.487.
- ↑ 13,0 13,1 Cabrera, Blas «First Results from a Superconductive Detector for Moving Magnetic Monopoles» (en anglès). Physical Review Letters, 48(20), 17-05-1982, pàg. 1378-1381. Bibcode: 1982PhRvL..48.1378C. DOI: 10.1103/PhysRevLett.48.1378.
- ↑ Milton, 2006, p. 60.
- ↑ 15,0 15,1 Polchinski, Joseph «Monopoles, Duality, and String Theory» (en anglès). International Journal of Modern Physics A, 19 (supp. 01), 01-02-2004, pàg. 145-154. arXiv: hep-th/0304042. Bibcode: 2004IJMPA..19S.145P. DOI: 10.1142/S0217751X0401866X.
- ↑ 16,0 16,1 «Magnetic Monopoles Detected in a Real Magnet for the First Time» (en anglès). Science Daily, 04-09-2009.
- ↑ 17,0 17,1 «Making magnetic monopoles, and other exotica, in the lab» (en anglès). Symmetry Breaking, 29-06-2009.
- ↑ 18,0 18,1 «Magnetic monopoles spotted in spin ices» (en anglès). Physics World, 03-09-2009. «Oleg Tchernyshyov de la Universitat Johns Hopkins (un investigador en aquest camp) adverteix que la teoria i els experiments són específics dels gels de spin, i que no és probable que aportin llum sobre els monopols magnètics tal com va predir Dirac.»
- ↑ 19,0 19,1 Gibney, Elizabeth «Quantum cloud simulates magnetic monopole». Nature, 29-01-2014. DOI: 10.1038/nature.2014.14612. «No és la primera vegada que els físics creen monopols anàlegs. El 2009, els físics van observar monopols magnètics en un material cristal·lí anomenat gel de spin, que, quan es refreda al voltant del zero absolut, sembla omplir-se de monopols clàssics de mida d'un àtom. Aquests són magnètics en un sentit real, però no es poden estudiar individualment. Anàlegs similars també s’han vist en altres materials, com en l’heli superfluid .... Steven Bramwell, físic de la University College de Londres qui va ser pioner en el treball sobre monopols en els gels de spint, diu que l'experiment (2014 dirigit per David Hall) va ser imprès, però que el que va observar no és un monopol de Dirac en la forma en què molta gent ho pot entendre. "Aquí hi ha una analogia matemàtica, bonica i ordenada. Però no són monopols magnètics.»
- ↑ Griffiths, 2013, p. 339.
- ↑ Parker, 1994.
- ↑ Mansfield i O'Sullivan, 2011.
- ↑ 23,0 23,1 23,2 Moulin, 2001, p. 869-877.
- ↑ Rindler, 1989, p. 993-994.
- ↑ Heras i Báez, 2009, p. 23-33.
- ↑ Shanmugadhasan, 1952, p. 218-225.
- ↑ 27,0 27,1 Fryberg, 1989, p. 125-159.
- ↑ 28,0 28,1 28,2 Jackson, 1999, p. secció 6.11.
- ↑ Jackson 1999, section 6.11, equation (6.153), page 275
- ↑ Arkani-Hamed et al., 2007, p. 060.
- ↑ Arkani-Hamed, 2007, p. 060.
- ↑ Zel'dovich i Khlopov, 1978, p. 239-241.
- ↑ Preskill, 1979, p. 1365-1368.
- ↑ Preskill, 1984, p. 461-530.
- ↑ Rees, 1998, p. 185.
- ↑ Brumfiel, Geoff «Physics: The waiting game» (en anglès). Nature, 429(6987), 06-05-2004, pàg. 10-11. Bibcode: 2004Natur.429...10B. DOI: 10.1038/429010a. PMID: 15129249.
- ↑ Álvarez, Luis W. «Analysis of a Reported Magnetic Monopole». A: Proceedings of the 1975 international symposium on lepton and photon interactions at high energies (en anglès), p. 967. «International symposium on lepton and photon interactions at high energies, Aug 21, 1975»
- ↑ Aad i et al., 2020, p. 031802.
- ↑ «If the structures of the magnetic fields appear to be magnetic monopoles, that are macroscopic in size, then this is a wormhole» (en anglès). All About Space, vol. 24 "Could wormholes really exist?", abril 2014.
- ↑ Dirac, Paul «Quantised Singularities in the Electromagnetic Field» (
 PDF) (en anglès). Proceedings of the Royal Society, 29-05-1931.
PDF) (en anglès). Proceedings of the Royal Society, 29-05-1931.
- ↑ Milstead, D; Weinberg, E. J. «Magnetic Monopoles» (
 PDF) (en anglès). Particle data group, agost 2015. «Fins ara no hi ha hagut observacions confirmades de partícules exòtiques amb càrrega magnètica.»
PDF) (en anglès). Particle data group, agost 2015. «Fins ara no hi ha hagut observacions confirmades de partícules exòtiques amb càrrega magnètica.»
- ↑ Rajantie, 2016, p. 40.
- ↑ Ollikainen et al., et al., p. 021023.
- ↑ Yakaboylu, E; Deuchert, A; Lemeshko, M «Emergence of Non-Abelian Magnetic Monopoles in a Quantum Impurity Problem» (en anglès). Physical Review Letters, 119(23), 06-12-2017, pàg. 235301. arXiv: 1705.05162. Bibcode: 2017PhRvL.119w5301Y. DOI: 10.1103/PhysRevLett.119.235301. PMID: 29286703.
- ↑ 45,0 45,1 Gibney, Elizabeth «Quantum cloud simulates magnetic monopole» (en anglès). Nature, 29-01-2014. DOI: 10.1038/nature.2014.14612.
- ↑ «Artificial magnetic monopoles discovered». Science Daily.
- ↑ Zhong et al., et al., p. 92-95.
- ↑ Qui et al., 2009, p. 1184-1187.
- ↑ 49,0 49,1 Bramwell, S. T; Giblin, S. R; Calder, S; Aldus, R; et al. «Measurement of the charge and current of magnetic monopoles in spin ice» (en anglès). Nature, 461(7266), 15-10-2009, pàg. 956-959. arXiv: 0907.0956. Bibcode: 2009Natur.461..956B. DOI: 10.1038/nature08500. PMID: 19829376.
- ↑ «'Magnetricity' Observed And Measured For First Time» (en anglès). Science Daily, 15-10-2009.
- ↑ 51,0 51,1 Giblin, S. R; Bramwell, S. T; Holdsworth, P. C. W; Prabhakaran, D; Terry, I «Creation and measurement of long-lived magnetic monopole currents in spin ice» (en anglès). Nature Physics, 7(3), 13-02-2011, pàg. 252-258. Bibcode: 2011NatPh...7..252G. DOI: 10.1038/nphys1896.
- ↑ Gingras, 2009, p. 375-376.
- ↑ Tennant, D. J. P; Grigera, S. A; Klemke, B; et al. «Dirac Strings and Magnetic Monopoles in Spin Ice Dy₂Ti₂O₇» (en anglès). Science, 326(5951), 03-09-2009, pàg. 411-444. arXiv: 1011.1174. Bibcode: 2009Sci...326..411M. DOI: 10.1126/science.1178868. PMID: 1972961.
- ↑ Pietilä i Möttönen, 2009.
Bibliografia[modifica]
- Aad, Georges; et al. «Search for magnetic monopoles and stable high-electric-charge objects in 13 TeV proton-proton collisions with the ATLAS detector» (en anglès). Phys. Rev. Lett., 124(3), 2020. arXiv: 1905.10130. Bibcode: 2020PhRvL.124c1802A. DOI: 10.1103/PhysRevLett.124.031802. PMID: 32031842.
- Arkani-Hamed, Nima; Motl, Luboš; Nicolis, Alberto; Vafa, Cumrun «The string landscape, black holes and gravity as the weakest force» (en anglès). Journal of High Energy Physics, 2007(6), 2007. arXiv: hep-th/0601001. Bibcode: 2007JHEP...06..060A. DOI: 10.1088/1126-6708/2007/06/060.
- Brau, Charles A. Modern Problems in Classical Electrodynamics. Oxford University Press, 2004. ISBN 978-0-19-514665-3.
- Chisholm, Hugh. The Encyclopaedia Britannica: A Dictionary of Arts, Sciences, Literature and General Information (en anglès). Cambridge University Press, 2018.
- Curie, Pierre «Sur la possibilité d'existence de la conductibilité magnétique et du magnétisme libre» (en francès). Séances de la Société Française de Physique [París], 1894.
- Dirac, Paul «Quantised Singularities in the Electromagnetic Field» (
 PDF) (en anglès). Proc. Roy. Soc. [Londres], A 133(60), 1931.
PDF) (en anglès). Proc. Roy. Soc. [Londres], A 133(60), 1931. - Fryberger, David «On Generalized Electromagnetism and Dirac Algebra» (
 PDF) (en anglès). Foundations of Physics, 19(2), febrer 1989. Bibcode: 1989FoPh...19..125F. DOI: 10.1007/bf00734522.
PDF) (en anglès). Foundations of Physics, 19(2), febrer 1989. Bibcode: 1989FoPh...19..125F. DOI: 10.1007/bf00734522. - Gingras, M. J. P «Observing Monopoles in a Magnetic Analog of Ice» (en anglès). Science, 326(5951), 2009. arXiv: 1005.3557. DOI: 10.1126/science.1181510. PMID: 19833948.
- Griffiths, David J. Introduction to electrodynamics (en anglès). Boston: Pearson, 2013. ISBN 978-0-321-85656-2.
- Heras, J. A.; Báez, G «The covariant formulation of Maxwell's equations expressed in a form independent of specific units» (en anglès). European Journal of Physics, 30(1), 2009. arXiv: 0901.0194. Bibcode: 2009EJPh...30...23H. DOI: 10.1088/0143-0807/30/1/003.
- Hitchin, N. J; Murray, M. K «Spectral curves and the ADHM method» (en anglès). Comm. Math. Phys., 114(3), 1988, pàg. 463-474. Bibcode: 1988CMaPh.114..463H. DOI: 10.1007/BF01242139.
- Hooper, Dan. Dark Cosmos: In Search of Our Universe's Missing Mass and Energy (en anglès). Harper Collins, 2009. ISBN 9780061976865.
- Jackson, John David. Classical Electrodynamics (en anglès). Nova York: Wiley, 1999. ISBN 978-0-471-30932-1.
- Kadowaki, H; Doi, N; Aoki, Y; Tabata, Y; et al. «Observation of Magnetic Monopoles in Spin Ice» (en anglès). Journal of the Physical Society of Japan, 78(10), 2009, pàg. 103706. arXiv: 0908.3568. Bibcode: 2009JPSJ...78j3706K. DOI: 10.1143/JPSJ.78.103706.
- Magie, William Francis. Principles of Physics: Designed for Use as a Textbook of General Physics (en anglès). Century Company, 2018.
- Mansfield, M; O'Sullivan, C. Understanding Physics (en anglès). John Wiley & Sons, 2011. ISBN 978-0-47-0746370.
- Milton, Kimball A «Theoretical and experimental status of magnetic monopoles» (en anglès). Reports on Progress in Physics, 69(6), 2006, pàg. 1637-1711. arXiv: hep-ex/0602040. Bibcode: 2006RPPh...69.1637M. DOI: 10.1088/0034-4885/69/6/R02.
- Moulin, F «Magnetic monopoles and Lorentz force» (en anglès). Nuovo Cimento B, 116(8), 2001, pàg. 869-877. arXiv: math-ph/0203043. Bibcode: 2001NCimB.116..869M.
- Ollikainen, T; Tiurev, K; Blinova, A; Lee, W; et al. «Experimental Realization of a Dirac Monopole through the Decay of an Isolated Monopole» (en anglès). Phys. Rev. X, 7(2), 2017, pàg. 021023. arXiv: 1611.07766. Bibcode: 2017PhRvX...7b1023O. DOI: 10.1103/PhysRevX.7.021023.
- Parker, C. B. McGraw-Hill Encyclopaedia of Physics (en anglès). McGraw-Hill, 1994. ISBN 978-0-07-051400-3.
- Pietilä, Ville; Möttönen, Mikko «Creation of Dirac Monopoles in Spinor Bose–Einstein Condensates» (en anglès). Phys. Rev. Lett., 103(3), 2009, pàg. 030401. arXiv: 0903.4732. Bibcode: 2009PhRvL.103c0401P. DOI: 10.1103/physrevlett.103.030401. PMID: 19659254.
- Preskill, John «Cosmological production of superheavy magnetic monopoles» (
 PDF) (en anglès). Phys. Rev. Lett., 43(19), 1979. Bibcode: 1979PhRvL..43.1365P. DOI: 10.1103/PhysRevLett.43.1365.
PDF) (en anglès). Phys. Rev. Lett., 43(19), 1979. Bibcode: 1979PhRvL..43.1365P. DOI: 10.1103/PhysRevLett.43.1365. - Preskill, John «Magnetic Monopoles» (en anglès). Annu. Rev. Nucl. Part. Sci., 34(1), 1984. Bibcode: 1984ARNPS..34..461P. DOI: 10.1146/annurev.ns.34.120184.002333.
- Qi, X. L; Li, R; Zang, J; Zhang, S C «Inducing a Magnetic Monopole with Topological Surface States» (en anglès). Science, 323(5918), 2009, pàg. 1184-1187. arXiv: 0811.1303. Bibcode: 2009Sci...323.1184Q. DOI: 10.1126/science.1167747. PMID: 19179491.
- Rajantie, Arttu «The search for magnetic monopoles» (en anglès). Physics Today, 69(10), 2016. Bibcode: 2016PhT....69j..40R. DOI: 10.1063/PT.3.3328.
- Ray, M. W; Ruokokoski, E.; Kandel, S; Möttönen, M; Hall, D. S «Observation of Dirac monopoles in a synthetic magnetic field» (en anglès). Nature, 505(7485), 2014. arXiv: 1408.3133. Bibcode: 2014Natur.505..657R. DOI: 10.1038/nature12954. ISSN: 0028-0836. PMID: 24476889.
- Rees, Martin. Before the Beginning (en anglès). Nova York: Basic Books, 1998. ISBN 0-201-15142-1.
- Rindler, Wolfgang «Relativity and electromagnetism: The force on a magnetic monopole» (en anglès). American Journal of Physics, 57(11), novembre 1989, pàg. 993-994. Bibcode: 1989AmJPh..57..993R. DOI: 10.1119/1.15782.
- Shanmugadhasan, S «The Dynamical Theory of Magnetic Monopoles» (en anglès). Canadian Journal of Physics, 30(3), 1952, pàg. 218-225. Bibcode: 1952CaJPh..30..218S. DOI: 10.1139/p52-021.
- Shnir, Yakov M. Magnetic Monopoles (en anglès). Springer-Verlag, 2005. ISBN 978-3-540-25277-1.
- Sutcliffe, P. M «BPS monopoles» (en anglès). Int. J. Mod. Phys. A, 12(26), 1997, pàg. 4663-4706. arXiv: hep-th/9707009. Bibcode: 1997IJMPA..12.4663S. DOI: 10.1142/S0217751X97002504.
- Vonsovsky, Sergey V. Magnetism of Elementary Particles (en anglès). Mir Publishers, 1975.
- Zel'dovich, Ya. B; Khlopov, M. Yu «On the concentration of relic monopoles in the universe» (en anglès). Phys. Lett., B79(3), 1978. Bibcode: 1978PhLB...79..239Z. DOI: 10.1016/0370-2693(78)90232-0.
- Zhong, Fang; Nagosa, Naoto; Takahashi, Mei S; Asamitsu, Atsushi; et al. «The Anomalous Hall Effect and Magnetic Monopoles in Momentum Space» (en anglès). Science, 302(5642), 2003. arXiv: cond-mat/0310232. Bibcode: 2003Sci...302...92F. DOI: 10.1126/science.1089408. PMID: 14526076.
Vegeu també[modifica]
Enllaços externs[modifica]
- «Magnetic Monopole Searches (lecture notes)» (en anglès).
- «Particle Data Group summary of magnetic monopole search» (
 PDF) (en anglès).
PDF) (en anglès). - «'Race for the Pole' Dr David Milstead». Vega Science Trust and the BBC/OU.
- «Interview with Jonathan Morris about magnetic monopoles and magnetic monopole quasiparticles» (en anglès). Drillingsraum, 16-04-2010.
- Brumfiel, Geoff. «'Overwhelming' evidence for monopoles» (en anglès). Nature, 2009.
- «Magnetic Monopoles Detected In A Real Magnet For The First Time» (en anglès). Science Daily, 2009.


























![{\displaystyle {\frac {dp_{\alpha }}{d\tau }}=\left[q_{\mathrm {e} }F_{\alpha \beta }+q_{\mathrm {m} }{{\tilde {F}}_{\alpha \beta }}\right]{\frac {v^{\beta }}{c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70c17f0719a56a90076101e31d85082dd48759cc)
![{\displaystyle {\frac {dp_{\alpha }}{d\tau }}=\left[q_{\mathrm {e} }F_{\alpha \beta }+{\frac {q_{\mathrm {m} }}{\mu _{0}c}}{{\tilde {F}}_{\alpha \beta }}\right]v^{\beta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99a66e59df2664591b5871472abefca529e9fea7)
![{\displaystyle {\frac {dp_{\alpha }}{d\tau }}=\left[q_{\mathrm {e} }F_{\alpha \beta }+{\frac {q_{\mathrm {m} }}{c}}{{\tilde {F}}_{\alpha \beta }}\right]v^{\beta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1408a51155c4cac826a7e1eb7f997172b5d516a1)













