Zero
 | |
| Tipus | non-positive integer (en) |
|---|---|
| Propietats | |
| Valor | 0 |
| Altres numeracions | |
| Binari | 02 |
| Hexadecimal | 016 |
El zero és tant un nombre com un numeral, que segueix el menys u i precedeix l'u. Permet quantificar la mida del conjunt buit, ja que un conjunt buit té zero elements. S'escriu 0 en les xifres àrabs i 〇 o 零 en les xineses.
Com a nombre, el zero és enter i parell. De vegades, tot i que no habitualment, el zero s'inclou dins el conjunt de nombres naturals.[1]
Propietats del zero[2][modifica]
A continuació, es descriuen algunes de les propietats bàsiques del nombre zero, vàlides per a nombres naturals, reals i complexos.
- En la suma, el zero és l'element neutre, és a dir, qualsevol nombre x, sumat amb 0 torna a donar x: .
- En el producte, qualsevol nombre operat amb el 0 dona 0: . Hom diu que el zero és l'element absorbent de l'operació producte.[3]
- En la divisió, zero dividit per qualsevol nombre dona zero: , per qualsevol x diferent de zero.
- També a la divisió i per x diferent de zero, o, cosa que és el mateix, no pot realitzar-se, ja que el zero no té invers multiplicatiu (és a dir, no existeix un nombre que multiplicat per zero doni x). Tot i això, el límit corresponent a aquesta operació, , tendeix a infinit.
- El cas restant de la divisió, és una indeterminació, és a dir, pot ser qualsevol nombre, ja que qualsevol nombre multiplicat per zero torna a donar zero.
- A la potència, , per qualsevol x diferent de zero, ja que per les propietats de les potències, .
- També a la potència i per x igual a zero, seguint la propietat anterior, , que, com hem demostrat anteriorment, és una indeterminació.
- La seva paritat és parella, és a dir, zero és un nombre parell, ja que compleix la definició de nombre parell .
En un grup additiu, l'element identitat s'anomena zero. En geometria, la dimensió d'un punt és zero.
Representacions del valor zero[4][modifica]
- Numeració maia:
 , al voltant del 400 a.C.
, al voltant del 400 a.C. - Numeració babilònica:
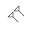 , al voltant del 400 a.C.
, al voltant del 400 a.C. - Numeració índia: ௦ (shunya chakra) o bé · (shunya bindu), al voltant del segle iii.
- Numeració xinesa: 〇 o 零, a partir del segle xii.
Etimologia[modifica]
La paraula zero va entrar al català a través de l'italià zero, una contracció de la forma veneciana zevero de l'italià zefiro, de l'àrab ṣifr (صفر),[5] que tenia el significat de "buit" i va evolucionar fins a significar zero quan es va utilitzar per traduir śūnya (sànscrit: शून्य) de l'Índia. De l'italià va passar al francès, castellà, anglès i català.[6]
El matemàtic italià Leonardo de Pisa Fibonacci, que va créixer al nord d’Àfrica i se li atribueix la introducció del sistema decimal a Europa, va utilitzar el terme zephyrum, que es va convertir en zefiro en italià i després es va contraure a zero en venecià.[7]
Història del zero[8][modifica]
El zero com a numeral ha nascut quatre vegades al llarg de la història. En els sistemes de numeració posicional, com l'actual, resulta necessari tenir un símbol que marqui la manca de nombre per tal de poder diferenciar cada nombre del mateix nombre multiplicat per una potència de deu. Això va dur al sorgiment d'un signe que complís aquestes necessitats a quatre de les majors civilitzacions de la història: Babilònia, la Civilització Maia, l'Índia i la Xina.
No obstant això, aquest posicionador no era considerat un nombre, si no simplement una marca. El fet que el zero passés a ser considerat un nombre només va succeir a la Civilització Maia, que l'usava pel calendari, i a l'Índia, on el matemàtic Brahmagupta publicà el 628 d.C. el seu tractat Brahmasphutasiddhanta, on, entre altres coses, estudiava per primera vegada les operacions matemàtiques amb el zero, que anomenaven shunya, pel concepte budista del mateix nom i d'un significat filosòfic altament relacionat.
El sistema de numeració hindú va arribar al món àrab gràcies a Muhàmmad ibn Mussa al-Khwarazmí amb la seva obra Algoritmi, que sembla que ha estat la primera en què s'exposà sistemàticament el valor posicional dels nombres en el sistema decimal (inclòs el zero), a partir del sistema de numeració utilitzat a l'Índia.[9] Del mon islàmic va passar al món cristià durant les croades, impulsat especialment per Fibonacci. A Europa, el zero va trigar segles a ser usat amb normalitat, i no va ser acceptat completament fins a les obres de Newton o Leibniz, a finals del segle xvii.
El sistema de numeració Hindú-Àrab va arribar a l'Europa occidental al segle xi, a través d'Al-Andalus pels musulmans espanyols, juntament amb el coneixement de l'astronomia clàssica i instruments com l'astrolabi; A Gerbert d'Aurillac se li atribueix la reintroducció dels ensenyaments perduts a l'Europa catòlica. Per aquest motiu, els números es van conèixer a Europa com a "números aràbics". El matemàtic italià Leonardo de Pisa Fibonacci va ser fonamental per portar el sistema a les matemàtiques europees el 1202.[10]
El zero a Occident[modifica]
El nombre zero ja existia des de temps enrere, havia sigut descobert molt abans per la civilització grega, sols que es considerava un secret. Sempre s'ha dit que aquest era un invent relativament modern, que cap civilització mediterrània el coneixia i per aquest motiu molts d'ells empraven sistemes de numeració agregativa.[11] No obstant, hi ha constància de que, els pitagòrics, deixebles del filòsof i matemàtic Pitàgores i l'escola que creà, amagaven l'existència d'aquest número. Es tractava d'una societat secreta que es dedicava a descobrir els secrets que amagaven les matemàtiques i el descobriment dels números perfectes resultà tota una aventura per a ells. Per aquest motiu, el fet de trobar els números irracionals fou una ruptura completa dels seus esquemes, resultà un fracàs i una destrucció absoluta del que coneixien fins al moment.
El descobriment d'aquest suposava una amenaça completament per a la seua concepció del món i les seues teories i estructures matemàtiques perfectes. Aquest problema sorgí en tractar d'aplicar el seu teorema al càlcul d'un triangle isòsceles del qual el catet diferent siga 1. El resultat era un nombre irrascional amb decimals infinits i, la falta de precisió fent-lo inexpressable, feu que commocionara tota l'escola i els seus coneixements pel fet que ja no eren capaços d'explicar clarament la concepció dels números racionals i aquesta mena de secta tractà d'amagar aquests junt als números imaginaris, negatius i zero, que consideraven absurds. S'arribà a dir que aquest descobriment fou l causa de la desaparició de l'escola i la mort d'aquells que divulgaren aquesta informació, pues es dedicaren a evitar que el coneixement de la seua existència sortira a la llum i, per tant, el sorgiment del zero no es produïra, no podien concebir que aquest número significara l'existència de "res", resultava controvertit i contrari als ideals que defenien. Es postergà fins que interveniren civilitzacions posteriors.[12]
Física[modifica]
El valor zero té un paper especial per a moltes magnituds físiques. Per a algunes quantitats, el nivell zero es distingeix naturalment de tots els altres nivells, mentre que per a altres s'escull més o menys arbitràriament. Per exemple, per a una temperatura absoluta (mesurada en kèlvins), el zero és el valor més baix possible (es defineixen temperatura negativas, però els sistemes de temperatura negativa no són realment més freds). Això contrasta, per exemple, amb les temperatures a l'escala Celsius, on el zero es defineix arbitràriament en el punt de congelació de l'aigua. Mesurant la intensitat del so en decibels o fons, el nivell zero s'estableix arbitràriament en un valor de referència, per exemple, en un valor per al llindar d'audició. En física, l'energia del punt zero és l'energia més baixa possible que pot tenir un sistema físic mecànic quàntic i és l'energia de l'estat fonamental del sistema.
Química[modifica]
El zero s'ha proposat com el nombre atòmic de l'element teòric tetraneutró. S'ha demostrat que un cúmul de quatre neutrons pot ser prou estable per ser considerat un àtom per dret propi. Això crearia un element sense protonss i sense càrrega al seu nucli.
Ja l'any 1926, Andreas von Antropoff va encunyar el terme neutroni per a una forma conjecturada de matèria formada per neutrons sense protons, que va col·locar com a element químic de nombre atòmic zero al capdavant del seu nova versió de la taula periòdica. Posteriorment es va col·locar com a gas noble enmig de diverses representacions en espiral del sistema periòdic de classificació dels elements químics.
Informàtica[modifica]
La pràctica més habitual al llarg de la història de la humanitat ha estat començar a comptar a un, i aquesta és la pràctica en els primers llenguatges clàssics de programació d'ordinadors com Fortran i COBOL. Tanmateix, a finals de la dècada de 1950, LISP va introduir la numeració basada en zero per a matrius, mentre que Algol 58 va introduir una base completament flexible per als subíndexs de matriu (permetent qualsevol nombre enter positiu, negatiu o zero com a base per a subíndex de matriu), i la majoria dels llenguatges de programació posteriors van adoptar una o una altra d'aquestes posicions. Per exemple, els elements d'un matriu es numeren a partir de 0 en C, de manera que per a una matriu d'n elements la seqüència de la matriu índexs va de 0 a n−1.
Pot haver-hi confusió entre la indexació basada en 0 i 1; per exemple, el JDBC de Java indexa els paràmetres des de l'1 encara que el mateix Java fa servir una indexació basada en 0.[13]
A les bases de dades, és possible que un camp no tingui valor. Aleshores es diu que té un valor nul.[14] Per als camps numèrics no és el valor zero. Per als camps de text, això no està en blanc ni la cadena buida. La presència de valors nuls condueix a la lògica de tres valors. Ja no és una condició ni vertadera ni falsa, però pot ser indeterminada. Qualsevol càlcul que inclogui un valor nul ofereix un resultat nul.[15]
Un punter nul és un punter d'un programa informàtic que no apunta a cap objecte o funció.
En binari, 0 representa el valor de "desactivat", el que significa que no hi ha flux elèctric.[16]
Zero és el valor de false en molts llenguatges de programació.
L'hora Unix (la data i l'hora associades amb una marca de temps zero) comença la mitjanit abans del primer de gener de 1970.[17][18][19]
L'època del Mac OS clàssic i Palm OS (la data i l'hora associades amb una marca de temps zero) comença la mitjanit abans del primer de gener de 1904.[20]
Els programadors sovint utilitzen un zero amb barra (0̸ ) per evitar confusions amb la lletra "O".[21]
Numeració dels anys[modifica]
A l'era del calendari aC., l'any 1 aC és el primer any abans del 1 dC; no hi ha un any zero. Per contra, a la numeració astronòmica dels anys, l'any 1 aC es numera 0, l'any 2 aC es numera -1, i així successivament.[22] També hi ha un any zero en la major part dels calendaris budistes i hindús.
Referències[modifica]
- ↑ Weisstein, Eric W. «Natural Number» (en anglès). MathWorld. Wolfram Research, Inc.. [Consulta: 27 novembre 2013].
- ↑ Ifrah, Georges. Historia universal de las cifras (en castellà). Segona. París: Espasa Fòrum, Desembre, 1997, p. 1434. ISBN 84-239-9730-8.
- ↑ «Propiedades algebraicas de la suma y el producto» (
 PDF). Universitat de València.
PDF). Universitat de València.
- ↑ Ifrah, Georges. Historia universal de las cifras (en espanyol). Segona. París: Espasa Fòrum, Desembre, 1997, p. 373-376, 735-740, 904. ISBN 84-239-9730-8.
- ↑ Menninger, Karl. Number words and number symbols: a cultural history of numbers (en anglès). Courier Dover Publications, 1992, p. 399–404. ISBN 978-0-486-27096-8.
- ↑ «zero». diccionari.cat. [Consulta: 29 setembre 2023].
- ↑ Ifrah, Georges. The Universal History of Numbers: From Prehistory to the Invention of the Computer (en anglès). John Wiley & Sons, 2000. ISBN 978-0-471-39340-5.
- ↑ Seife, Charles. Zero, the biography of a dangerous idea (en anglès). Primera. Londres: Souvenir Press, 2000. ISBN 978-0-285-63594-4.
- ↑ Brezina, Corona. Al-Khwarizmi: The Inventor Of Algebra (en anglès). Al-Khwarizmi: The Inventor Of Algebra, 2006, p.95. ISBN 1404205136.
- ↑ Howard, Eves. An Introduction to the History of Mathematics (en anglès). 6a ed.). Brooks Cole, 1990, p. 261. ISBN 0-03-029558-0.
- ↑ «La historia del cero y otros números “raros”» (en castellà), 07-03-2020. [Consulta: 15 desembre 2021].
- ↑ «Robert Musil se encuentra con los pitagóricos y su contratiempo con los números irracionales» (en castellà), 18-10-2020. [Consulta: 15 desembre 2021].
- ↑ «ResultSet (Java Platform SE 8 )». Arxivat de l'original el 9 maig 2022. [Consulta: 9 maig 2022].
- ↑ Wu, X.; Ichikawa, T.; Cercone, N. Knowledge-Base Assisted Database Retrieval Systems (en anglès). World Scientific, 25 octubre 1996. ISBN 978-981-4501-75-0 [Consulta: 7 novembre 2020].
- ↑ «Null values and the nullable type», 12-12-2018. Arxivat de l'original el 23 novembre 2021. [Consulta: 23 novembre 2021]. «In regard to services, sending a null value as an argument in a remote service call means that no data is sent. Because the receiving parameter is nullable, the receiving function creates a new, uninitialized value for the missing data then passes it to the requested service function.»
- ↑ Chris Woodford, 2006, p. 9.
- ↑ Paul DuBois. "MySQL Cookbook: Solutions for Database Developers and Administrators" Arxivat 24-2-2017 a Wayback Machine. 2014. p. 204.
- ↑ Arnold Robbins; Nelson Beebe. "Classic Shell Scripting" Arxivat 24-2-2017 a Wayback Machine.. 2005. p. 274
- ↑ Iztok Fajfar. "Start Programming Using HTML, CSS, and JavaScript" Arxivat 24-2-2017 a Wayback Machine.. 2015. p. 160.
- ↑ Darren R. Hayes. "A Practical Guide to Computer Forensics Investigations" Arxivat 24-2-2017 a Wayback Machine.. 2014. p. 399
- ↑ «Font Survey: 42 of the Best Monospaced Programming Fonts», 18-08-2010. Arxivat de l'original el 24 gener 2012. [Consulta: 22 juliol 2021].
- ↑ Steel, Duncan. Marking time: the epic quest to invent the perfect calendar. John Wiley & Sons, 2000, p. 113. ISBN 978-0-471-29827-4. «In the B.C./A.D. scheme there is no year zero. After 31 December 1 BC came 1 January AD 1. ... If you object to that no-year-zero scheme, then don't use it: use the astronomer's counting scheme, with negative year numbers.»
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Zero |
- Searching for the World's First Zero (anglès)
- Edsger Dijkstra: Why numbering should start at zero (anglès)











