Angle

∠, el símbol Unicode per a l'angle és l'U+2220

En geometria, un angle és una figura geomètrica formada per dues semirectes d'origen comú (el vèrtex de l'angle). També s'anomena angle la regió compresa entre aquestes semirectes. La magnitud de l'angle és la «quantitat de rotació» que separa les dues rectes, i es pot mesurar considerant l'amplitud de l'arc circular format quan es rota una semirecta al voltant del vèrtex fins que coincideix amb l'altra semirecta. Quan no hi ha possibilitat de confusió, el terme "angle" s'usa indistintament tant per la configuració geomètrica com per la seva magnitud angular, que és simplement una quantitat numèrica.

La paraula angle prové del llatí angulus, que significa "racó"; angulus és un diminutiu la forma primitiva del qual, angus, no prové del llatí, sinó del grec antic ἀγκύλος (ankylοs), que significa "encorbat" que, al seu torn, està relacionat amb l'arrel protoindoeuropeu *ank-, que significa "doblegar" o "arquejar".

Definició i característiques

Els quatre angles formats per dues rectes secants

Les busques d'un rellotge conformen diferents tipus d'angles. en aquest cas, un angle agut.

Existeixen dues maneres de definir un angle:

1. Segons la forma geomètrica: S'anomena "angle" a l'amplitud entre dues línies de qualsevol tipus que concorren en un punt comú anomenat vèrtex. Col·loquialment, angle és la figura formada por dues línies amb origen comú. L'angle entre dos corbes és l'angle que formen les seves rectes tangent en el punt de intersecció.
2. Segons la forma trigonomètrica: És l'amplitud de rotació o gir que descriu un segment rectilini entorn d'un dels seus extrems agafant com a vèrtex des d'una posició inicial fins una posició final. Si la rotació és en sentit levogir (contrari a les busques del rellotge), l'angle es considera positiu. Si la rotació és en sentit dextrogir (conforme a les busques del rellotge), l'angle es considera negatiu.

Definicions clàssiques

Euclides definí l'angle pla com la inclinació en un pla de dues línies que es tallen i que no són parel·leles. Segons Procle, un angle ha de ser o bé una qualitat o quantitat, o bé una relació. El primer concepte fou usat per Eudem de Rodes, que explicava l'angle com una desviació de la recta; el segon, per Carp d'Antioquia, que el veia com un interval o espai entre línies secants; i finalment, el tercer fou usat per Euclides, tot i que les seves definicions d'angle obtús, recte i agut són certament quantitatives.

Regió angular

Es denomina regió angular a cada una de les quatre parts il·limitades en que queda dividit un pla per dos rectes que es tallen. Aquests angles es mesuren d'acord amb la seva àrea similitudinal. Existeixen realment diferents angles anomenats convexos i còncaus. Se'ls anomena així perquè varia la mesura de l'angle que es relacionen una mica amb l'angle recte, obtús i sobretot oblic.

Unitats de mesures d'angles

Definició del radian, l'angle quan tenim un arc de longitud igual al radi.

En anàlisi dimensional l'obertura dels angles és una magnitud física que es pot mesurar de diferents maneres. Al Sistema Internacional, la unitat per a mesurar els angles és el radian (també es pot escriure radiant), una unitat derivada sense dimensions. Hi ha d'altres unitats per mesurar els angles, a més del radiant una de les més utilitzades és el grau. Bàsicament hi ha dues maneres de definir les unitats utilitzades per a mesurar els angles:

1. Amb el quocient entre la longitud (l) de l'arc limitat pels dos costats de l'angle d'una circumferència centrada al vèrtex i el seu radi (r).

• Radian: Aquest quocient és independent del radi de la circumferència i no té unitats. Tanmateix se sol indicar amb la pseudounitat radian (rad). ${\phi}=\frac{l}{r}$. Els radians són molt usats en matemàtiques ja que no necessiten d'una convenció arbitrària i les funcions trigonomètriques presenten desenvolupaments senzills en sèrie de Taylor si el seu argument és expressat en radians. És per això que és la pseudounitat del Sistema Internacional d'Unitats.

2. Comparant-lo amb alguna divisió d'algun angle notable. Les comparacions més usuals són:

• Grau: El grau sexagesimal de símbol º és la norantena part d'un angle recte. En aquest cas, per subdivisions del grau sexagesimal, usualment s'utilitza la seixantena part del grau sexagesimal, el minut (') i la seixantena part del minut, el segon ("). Els graus sexagesimals són els més usats en la vida quotidiana tot i que no tenen cap propietat interessant.
• El grau centesimal o gon i de símbol ^g o ^G és la centena part d'una angle recte. Per a subdivisions del grau centesimal, usualment s'utilitza la centena part del grau centesimal, el minut (^m o ^c) i la centena part del minut, el segon (^s o ^cc). Els graus centesimals són molt usats en topografia ja que tenen la bona propietat de fer les divisions en base 100.

Algunes equivalències apareixen tot seguit:

• 180º $=200^g={\pi}$ rad$=\frac{1}{2}$volta sencera
• $1^g=100^m=10000^s=1^G=100^c=10000^{cc}$
• 1º = 60' = 3600"
• 1rad = 57º17'44.8..."

Les màquines de calcular solen usar els símbols R, D i G per referir-se a radians, graus sexagesimals (en anglès, degrees) i graus centesimals (en anglès, grads) respectivament.

També és freqüent en angles petits, sobretot per mesurar inclinacions respecte la horitzontal, l'ús de la tangent de l'angle, sovint indicada en forma de percentatge. Llavors, es parla més aviat de pendent o rampa, però també s'està mesurant l'obertura d'un angle. En aquest cas, la tangent té un avantatge clar, i és que és la raó entre la distància vertical i la horitzontal (per exemple un pendent 4% significa que es recorren 4 metres de distància vertical per cada 100 metres de distància horitzontal). La tangent, coincideix aproximadament amb l'angle en radians quan aquest és petit.

Triangle format amb tres angles aguts

Criteri de signes i altres convencions

En matemàtiques en el pla, universalment s'adopta el criteri de signes següent:

• Signe positiu per angles mesurats en sentit antihorari.
• Signe negatiu per angles mesurats en sentit horari.

En matemàtiques en el pla, a més, s'entén com a mesura de l'angle d'una recta a l'angle que forma aquesta amb l'eix d'abscisses.

Identificació d'angles

En les expressions matemàtiques, és comú l'ús de lletres gregues (α, β, γ, θ, φ, ...) per utilitzar-les com a variables de peu per la mida d'un angle. (Per evitar confusions amb el seu altre significat, el símbol π típicament no s'utilitza per a aquest propòsit.) Les lletres en minúscules romanes (a, b, c, ...) també s'utilitzen.

En les figures geomètriques, els angles també poden ser identificats per les etiquetes enganxades als tres punts que les defineixen. Per exemple, l'angle en el vèrtex A tancada pel les semirectes AB i AC (és a dir, les línies des del punt A al punt B i el punt A fins al punt C) es denota ∠ BAC o BAC. De vegades, on no hi ha cap risc de confusió, l'angle pot ser denominat simplement pel seu vèrtex ("angle A").

Classificació dels angles en aguts i obtusos

Angle obtús dins d'un triangle

Segons la seva comparació amb l'angle recte, els angles es classifiquen en:

• Angles aguts, si són estrictament menors que un angle recte.
• Angles obtusos, si són estrictament majors que un angle recte.

Angles notables

Els angles, segons la seva amplitud, s'anomenen:

Tipus	Descripció
Angle nul	L'angle nul és aquell que mesura 0º (complet però sense l'arc).
Angle agut	És l'angle format per dues semirectes amb una amplitud major de 0 rad i menor de $\frac{\pi}{2}$ rad. És a dir, major de 0° i menor de 90° (graus sexagesimals), o menor de 100g (graus centesimals).
Angle recte	L'angle recte és aquell que és igual al seu suplementari. Mesura 90 graus sexagesimals (º), 100 graus centesimals (g) o $\frac{{\pi}}{2}$ radians (rad) i és la meitat d'un angle pla. Dos angles que sumen un angle recte són complementaris. Els dos costats d'un angle recta són perpendiculars. La Projecció ortogonal d'un sobre l'altre és un punt, que coincideix amb el vèrtex.
Angle obtús	Un angle obtús té una amplitud més gran de $\frac{\pi}{2}$ rad i més petita que $\pi\,$ rad Major de 90° i menor de 180° sexagesimals (o més de 100g i menys de 200g centesimals).
Angle pla o estès o colinial	L'angle pla és l'angle limitat per dues semirectes oposades. Mesura 180º, 200g o ${\pi}$ rad. Dos angles que sumen un angle pla són suplementaris. Equivalent a 180° sexagesimals (o 200g centesimals).
Angle complet o perigonal	Un angle complet o perigonal, té una amplitud de $2\pi\,$ rad Equivalent a 360° sexagesimals (o 400g centesimals).

Angles convex i còncau

Tipus	Descripció
Angle convex	És el que mesura menys de $\pi\,$ rad. Equival a més de 0° i menys de 180°sexagesimals (o més de 0g i menys de 200g centesimals).
Angle còncau,	És el que mesura més de $\pi\,$ rad i menys de $2 \pi\,$ rad. Això és, mes de 180° i menys de 360° sexagesimals (o més de 200g i menys de 400g centesimals).

Angles relacionats

L'angle α és conjugat de β, aicí com β ho és d'α

Un parell d'angles α i β suplementaris

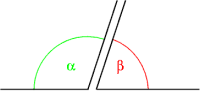
En funció de la seva posició s'anomenen:

• Angles adjacents: dos angles són adjacents quan els punts que els formen pertanyen a un mateix semiplà dels determinats per una de les rectes i a diferents semiplans dels determinats per l'altra recta.
• Angles consecutius: dos angles són consecutius quan tenen un vèrtex i un costat en comú.
• Angles oposats pel vèrtex: dos angles són oposats pel vèrtex quan els costats d'un són la prolongació dels de l'altre. Dos angles oposats pel vèrtex són iguals.
• Angles corresponents: dos angles són corresponents quan són formats per dues paral·leles i una transversal.

En funció de la seva amplitud es poden classificar en:

• Angles congruents: dos angles són congruents quan tenen la mateixa amplitud, que mesuren el mateix.
• Angles complementaris: dos angles són complementaris quan la suma de les mesures és π/2 radians o 90°.
• Angles suplementaris: dos angles són suplementaris quan la suma de les mesures és π radians o 180° (graus sexagesimals), o 400 graus centesimals. Així, per obtenir l'angle suplementari d'α, que té una amplitud de 120º, es restarà α de 180 °: β = 180° – 120° = 60°. Si dos angles són suplementaris de dos angles congruents, també són congruents entre si.
• Angles conjugats: dos angles són conjugats quan les mesures sumen 2π radians o 360° (graus sexagesimals), o 400 graus centesimals. Dos angles conjugats amb vèrtexs coincidents, tindran els seus costats comuns. Així, per obtenir l'angle conjugat d'α que té una amplitud de 250 °, es restarà α de 360 °: Β = 360 ° - 250 º = 110 º. L'angle β (beta) és el conjugat de l'angle α (alfa).

Suma d'angles interiors d'un polígon simple

En geometria euclidiana, la suma d'angles interiors d'un polígon simple d'n costats és de (n-2)·π radians o (n-2)·180º. Així, la suma d'angles interns d'un triangle és 180º i la d'un quadrilàter, 360º.

Angles respecte una circumferència

Cargol trisectriu

Els casos d'angle i circumferència fan referència als diferents noms que rep un angle segons la seva posició respecte a una circumferència, i els diferents teoremes que defineixen el seu valor respecte l'arc que abasten.

Angles tridimensionals

L'angle díedre és cada una de les dues parts de l'espai delimitades per dos semiplans que tenen una recta en comú.

L'angle sòlid és l'angle espacial que abasta un objecte vist des d'un punt donat, que mesura la mida aparent d'aquest objecte.

Coordenades angulars tridimensionals

Els angles d'Euler són tres coordenades angulars que indican la orientació d'un sistema de referència d'eixos ortogonals, normalment movible, respecte a un altre fixe.

Angles en un espai vectorial

Donat un espai vectorial, que el seu cos és el conjunt dels números reals i en el que existeix un producte escalar entre vectors $\langle\cdot,\cdot\rangle$, es defineix l'angle format per dos vectors no nuls $x$ i $y$ mitjançant l'expressió:
$\angle(x,y)=\arccos\frac{\langle x, y \rangle}{\|x\|\cdot\|y\|},$
Si el quocient anterior és 0, es diu que ambdós vectors són ortogonals o perpendiculars. El quocient anterior es troba a l'interval $(-1,1)$ a causa de la desigualtat de Cauchy-Schwarz, cosa que garanteix que sempre es pot aplicar l'arccosinus. Normalment, s'agafa la branca de l'arccosinus de forma que l'angle que formen dos vectors sempre està en el interval $[0,\pi]$ (geomètricament, s'escull l'angle més petit dels que formen els dos vectors). Les propietats principals que compleix l'angle entre dos vectors són les següents:

• Si multipliquem un dels vectors per un escalar positiu, l'angle no canvia.
• Si multipliquem un dels vectors per un escalar negatiu, l'angle passa a ser el complementari.
• Es compleix el teorema del cosinus, o sigui, donats $x$ i $y$ vectors no nuls,
  $\|x-y\|^2=\|x\|^2+\|y\|^2-2\|x\|\cdot\|y\|\cdot\cos\angle(x,y).$

Galeria d'angles

$0^{\circ}\,$	$15^{\circ}\,$	$30^{\circ}\,$	$45^{\circ}\,$	$60^{\circ}\,$	$75^{\circ}\,$
$90^{\circ}\,$	$105^{\circ}\,$	$120^{\circ}\,$	$135^{\circ}\,$	$150^{\circ}\,$	$165^{\circ}\,$
$180^{\circ}\,$	$195^{\circ}\,$	$210^{\circ}\,$	$225^{\circ}\,$	$240^{\circ}\,$	$255^{\circ}\,$
$270^{\circ}\,$	$285^{\circ}\,$	$300^{\circ}\,$	$315^{\circ}\,$	$330^{\circ}\,$	$345^{\circ}\,$
$360^{\circ}\,$

Vegeu també

• Casos d'angle i cercle
• Angle sòlid
• Nombre pi
• Trisecció de l'angle

Bibliografia

• Heiberg, Johan Ludvig. Heath, T.L.. Euclid. 1. Cambridge University press, 1908 (The thirteen books of Euclid's Elements). 
•  Aquest article incorpora text d'una publicació que es troba al domini públic: Chisholm, Hugh (1911). A: Encyclopædia Britannica (edició de 1911) (11a edició) (en anglès). Cambridge University Press. 

Enllaços externs

• «Demostració animada (Animació interactiva de les característiques dels angles suplementaris)» (en anglès).